Created
January 31, 2019 19:38
-
-
Save KelSolaar/53113ad0330010eed00062b9fcbf01e1 to your computer and use it in GitHub Desktop.
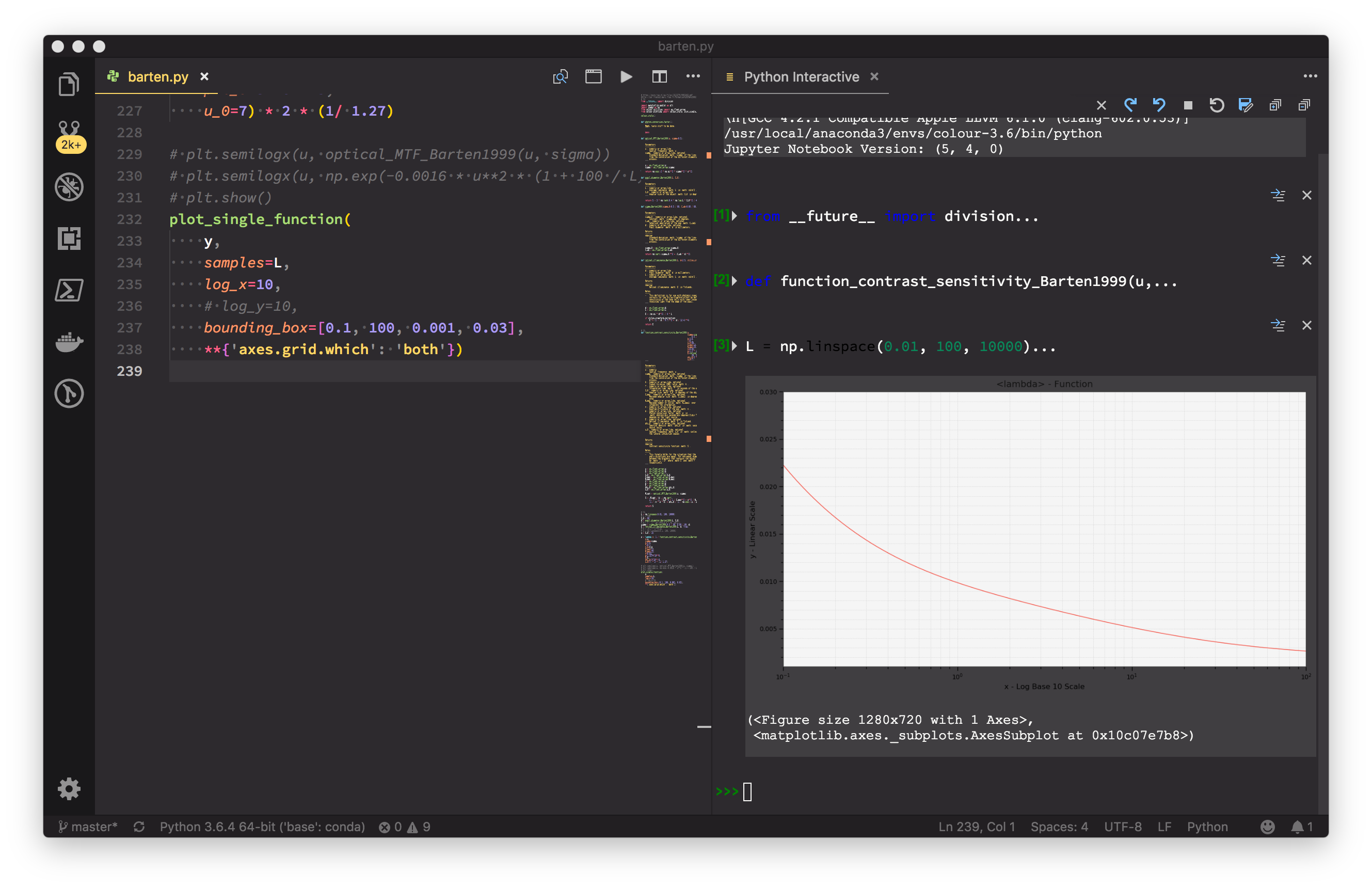
Contrast Sensitivity Function - Barten (1999)
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| # https://pure.tue.nl/ws/files/1613279/9901043.pdf | |
| #http://car.france3.mars.free.fr/Formation%20INA%20HD/HDTV/HDTV%20%202007%20v35/SMPTE%20normes%20et%20confs/Contrastm.pdf | |
| # %% | |
| from __future__ import division | |
| import matplotlib.pyplot as plt | |
| import numpy as np | |
| from colour.utilities import as_float_array | |
| from colour.plotting import colour_style, plot_single_function | |
| colour_style() | |
| def photon_conversion_factor(): | |
| """ | |
| Mmmh, tasty stuff to be done. | |
| """ | |
| pass | |
| def optical_MTF_Barten1999(u, sigma=0.5): | |
| """ | |
| Parameters | |
| ---------- | |
| u : numeric or array_like | |
| Spatial frequency :math:`u`. | |
| sigma : numeric or array_like, optional | |
| Standard deviation :math:`\sigma` of the line-spread function resulting | |
| from the convolution of the different elements of the convolution | |
| process. | |
| """ | |
| u = as_float_array(u) | |
| sigma = as_float_array(sigma) | |
| return np.exp(-2 * np.pi**2 * sigma**2 * u**2) | |
| def pupil_diameter_Barten1999(L, X_0): | |
| """ | |
| Parameters | |
| ---------- | |
| L : numeric or array_like | |
| Average luminance :math:`L` in :math:`cd/m^2`. | |
| X_0 : numeric or array_like | |
| Angular size of the object :math:`X_0` in degrees. | |
| """ | |
| return 5 - 3 * np.tanh(0.4 * np.log(L * X_0**2 / 40**2)) | |
| def sigma_Barten1999(sigma_0=0.5 / 60, C_ab=0.08 / 60, d=2.5): | |
| """ | |
| Parameters | |
| ---------- | |
| sigma_0 : numeric or array_like, optional | |
| Constant :math:`\sigma_{0}` in degrees. | |
| C_ab : numeric or array_like, optional | |
| Spherical aberration of the eye :math:`C_{ab}` in degrees. | |
| d : numeric or array_like, optional | |
| Pupil diameter :math:`d` in millimeters. | |
| Returns | |
| ------- | |
| ndarray | |
| Standard deviation :math:`\sigma` of the line-spread function resulting | |
| from the convolution of the different elements of the convolution | |
| process. | |
| """ | |
| sigma_0 = as_float_array(sigma_0) | |
| C_ab = as_float_array(C_ab) | |
| return np.sqrt((sigma_0)**2 + (C_ab * d)**2) | |
| def retinal_illuminance_Barten1999(L, d=2.5, stiles_crawford_correction=True): | |
| """ | |
| Parameters | |
| ---------- | |
| d : numeric or array_like | |
| Pupil diameter :math:`d` in millimeters. | |
| L : numeric or array_like | |
| Average luminance :math:`L` in :math:`cd/m^2`. | |
| Returns | |
| ------- | |
| ndarray | |
| Retinal illuminance :math:`E` in Trolands. | |
| Notes | |
| ----- | |
| - This definition is for use with photopic viewing conditions and thus | |
| corrects for the Stiles-Crawford effect by default, i.e. directional | |
| sensitivity of the cone cells with lower response of cone cells | |
| receiving light from the edge of the pupil. | |
| """ | |
| d = as_float_array(d) | |
| L = as_float_array(L) | |
| E = (np.pi * d**2) / 4 * L | |
| if stiles_crawford_correction: | |
| E *= (1 - (d / 9.7)**2 + (d / 12.4)**4) | |
| return E | |
| # %% | |
| def function_contrast_sensitivity_Barten1999(u, | |
| sigma=sigma_Barten1999( | |
| 0.5 / 60, 0.08 / 60, 3.0), | |
| k=3.0, | |
| T=0.1, | |
| X_0=60, | |
| X_max=12, | |
| N_max=15, | |
| n=0.03, | |
| p=1.2 * 10**6, | |
| E=retinal_illuminance_Barten1999( | |
| 20, 3), | |
| phi_0=3 * 10**-8, | |
| u_0=7): | |
| """ | |
| Parameters | |
| ---------- | |
| u : numeric | |
| Spatial frequency :math:`u`. | |
| sigma : numeric or array_like, optional | |
| Standard deviation :math:`\sigma` of the line-spread function resulting | |
| from the convolution of the different elements of the convolution | |
| process. | |
| k : numeric or array_like, optional | |
| Signal-to-noise (SNR) ratio :math:`k`. | |
| T : numeric or array_like, optional | |
| Integration time :math:`T` in seconds of the eye . | |
| X_0 : numeric or array_like, optional | |
| Angular size :math:`X_0` in degrees of the object. | |
| X_max : numeric or array_like, optional | |
| Maximum angular size :math:`X_{max}` in degrees of the integration | |
| area. | |
| N_max : numeric or array_like, optional | |
| Maximum number of cycles :math:`N_{max}` over which the eye can | |
| integrate the information. | |
| n : numeric or array_like, optional | |
| Quantum efficiency of the eye :math:`n`. | |
| p : numeric or array_like, optional | |
| Photon conversion factor :math:`p` in | |
| :math:`photons\div seconds\div degrees^2\div Trollands` that | |
| depends on the light source. | |
| E : numeric or array_like, optional | |
| Retinal illuminance :math:`E` in Troland. | |
| phi_0 : numeric or array_like, optional | |
| Spectral density :math:`\phi_0` in :math:`seconds degrees^2` of the | |
| neural noise. | |
| u_0 : numeric or array_like, optional | |
| Spatial frequency :math:`u_0` in :math:`cycles\div degrees` above which | |
| the lateral inhibition ceases | |
| Returns | |
| ------- | |
| ndarray | |
| Contrast sensitivity function :math:`S`. | |
| Notes | |
| ----- | |
| - This formula holds for the situation that the object dimensions in x | |
| and y directions are equal. For non-equal dimensions, the factor | |
| between the brackets that contains the object size has to be replaced | |
| by :math:`1 / XY` where :math`X` and :math`Y` are given by ... | |
| respectively. | |
| """ | |
| u = as_float_array(u) | |
| k = as_float_array(k) | |
| T = as_float_array(T) | |
| X_0 = as_float_array(X_0) | |
| X_max = as_float_array(X_max) | |
| N_max = as_float_array(N_max) | |
| n = as_float_array(n) | |
| p = as_float_array(p) | |
| E = as_float_array(E) | |
| phi_0 = as_float_array(phi_0) | |
| u_0 = as_float_array(u_0) | |
| M_opt = optical_MTF_Barten1999(u, sigma) | |
| S = (M_opt / k) / np.sqrt( | |
| 2 / T * (1 / X_0**2 + 1 / X_max**2 + u**2 / N_max**2) * | |
| (1 / (n * p * E) + phi_0 / (1 - np.exp(-(u / u_0)**2)))) | |
| return S | |
| # %% | |
| L = np.linspace(0.01, 100, 10000) | |
| # L = 500 | |
| X_0 = 60 | |
| d = pupil_diameter_Barten1999(L, X_0) | |
| # d = 5 - 3 * np.tanh(0.4 * np.log(L)) | |
| sigma = sigma_Barten1999(0.5 / 60, 0.08 / 60, d) | |
| E = retinal_illuminance_Barten1999(L, d, True) | |
| # E = 14.7 * L**0.83 | |
| # u = np.linspace(0.1, 100, 10000) | |
| u = X_0 / 15 | |
| y = lambda x: 1 / function_contrast_sensitivity_Barten1999( | |
| u=u, | |
| sigma=sigma, | |
| k=3.0, | |
| T=0.1, | |
| X_0=X_0, | |
| X_max=12, | |
| N_max=15, | |
| n=0.03, | |
| p=1.2274*10**6, | |
| E=E, | |
| phi_0=3*10**-8, | |
| u_0=7) * 2 * (1/ 1.27) | |
| # plt.semilogx(u, optical_MTF_Barten1999(u, sigma)) | |
| # plt.semilogx(u, np.exp(-0.0016 * u**2 * (1 + 100 / L)**0.08)) | |
| # plt.show() | |
| plot_single_function( | |
| y, | |
| samples=L, | |
| log_x=10, | |
| # log_y=10, | |
| bounding_box=[0.1, 100, 0.001, 0.03], | |
| **{'axes.grid.which': 'both'}) |
Author
KelSolaar
commented
Jan 31, 2019
Sign up for free
to join this conversation on GitHub.
Already have an account?
Sign in to comment