Skip to content

Instantly share code, notes, and snippets.

@koyumeishi

koyumeishi/readme.md

Created January 30, 2020 21:44
Show Gist options
  • Save koyumeishi/4275c679ab1c91275f2012fe62bec8e3 to your computer and use it in GitHub Desktop.
Save koyumeishi/4275c679ab1c91275f2012fe62bec8e3 to your computer and use it in GitHub Desktop.
Download ZIP
MM114 SnakeCharmer
Raw
readme.md

MM114 SnakeCharmer

概要

  • N*N のグリッド (N は奇数)
  • (floor(N/2), floor(N/2)) のセルからヘビが出てくる
  • ヘビは長さ NN で、頭..尾 を (0..NN-1) の離散的なパーツと考える
  • ヘビの頭(パーツ 0)は今いるセルに隣接するセル (上下左右) へ移動できる。 頭以外のパーツ i は パーツ i-1 があった場所へ移動する
  • ヘビは自分自身と重なったりグリッドの外へ出てはいけない
  • ヘビのパーツにはそれぞれ数が割り当てられている。 S[i] := パーツ i の数 (2<= S[i] <= 9)
  • ヘビが停止したときセル (x,y) に数字 z が書かれたパーツがあるとき、 
    Score = Σ z^((x,y) に隣接するセルにある z の数 + 1)
    がスコアとなる
  • シード毎に異なる値 V (3 <= V <= 9) があり、 S[i] は [2, V] から一様ランダムに選ばれる
  • N = [7, 49]
    => N*N = 49..2401

考察

  • 要するにパイプをスコアが高くなるように配置するゲーム
  • ヘビを全部出せば N*N セルに丁度埋まる。 使わないと一部空白になるが、多分勿体ないので基本的に全部使う前提で良いと思う
  • [2..9]^5 = [32, 243, 1024, 3125, 7776, 16807, 32768, 59049]
  • [2..9]^4 = [16, 81, 256, 625, 1296, 2401, 4096, 6561]
  • [2..9]^3 = [8, 27, 64, 125, 216, 343, 512, 729]
  • [2..9]^2 = [4, 9, 16, 25, 36, 49, 64, 81]
  • ヘビの頭 - 中央のセル がつながっていると思うと、 ヘビの配置は一つの閉路になる
  • (A) ヘビを順に伸ばす手法　(尻尾から決めていく探索系) -> デッドスペースが生えると計算が狂う (頭まで配置する前提だと死地生じてはいけない。 あらかじめいくつか使わない前提ならアリだけど、多分勿体ない。 隣接セルは 2..4 しかないので、一か所死ぬと 2..4 接続損する)
  • (B) 一つの配置から接続をつなぎかえる手法 (焼き鈍し系) -> 接続が変わる -> ヘビの順番が変わるのでかなり大きく盤面が変わってしまう

A は

  • 序盤スコアが定まりにくい (= 評価関数がボロボロ)
  • 死地が大量に生えそう って感じで微妙。

B はやり方がいくつか考えられるけど、

  1. 盤面を適当なサイズの小グリッドに区切って、 入出セルの位置を変えずに繋ぎかえる
  2. 大きな閉路だと思って辺の交換で閉路を壊さずに繋ぎかえる

1 は例えば M*M を切り取って

$@>>v
^<v<v
$^<^v
^<>^v
@^^<<

のようなところから 入出セル(@,$)を変えずに組み替える

  • n系統の入出があるとその関係を壊さずにつなげると窮屈
    細長い直線のようなものがあるとそもそも無理
  • 系統の入出関係に制限を設けないと外側も崩れる (ヘビの順番が変わるので)

2 は閉路のつなぎ替え -> TSP における辺の交換と似ている
=> 2-opt, double bridge でつなぎ替えをする

  • 圧倒的にシンプル。 ただのグラフだと思えば何も特殊なところはない。 配置の合法性も保たれる
    繋ぎかえる区間長を短くすれば全体を大きく壊すこともない。 これやな

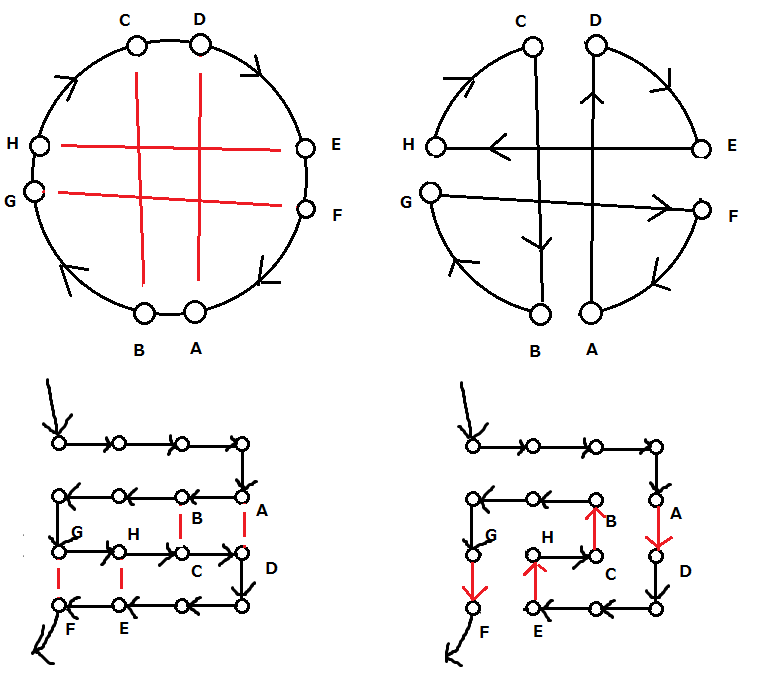
グリッドグラフなので 2-opt, double bridge と辺の関係性は以下のようになる

2-opt

A->B     A  B
      => |  |
         v  v
D->C     D  C
  • 順平行な辺の組に適用される
  • B->D の関係が反転され B<-D となる ABDCA => ADBCA
  • 以下のようにして頭 -> 尻尾の接続も変更が可能
T..S     T  S
      => |  .
         v  .
U->V     U  V

Double Bridge

A->B     A  B  |  E->F     E  F
      => |  ^  |        => |  ^
         v  |  |           v  |
D<-C     D  C  |  H<-G     H  G
  • 逆平行な2組の辺に適用される
  • BG, DE 区間がswap される。 ABGHCDEF -> ADEHCBGF

更新のときは double bridge ばかり採用される。 謎。
7*7 は空間が小さいからか焼き鈍しより乱択の方が強そう
初期状態、提供されているコードにもあるような渦巻き

*-*-*-*-*-*-*
|           
* *-*-*-*-*-*
| |         |
* * *-*-*-* *
| | |     | |
* * * *-* * *
| | |   | | |
* * *-*-* * *
| |       | |
* *-*-*-*-* *
|           |
*-*-*-*-*-*-*

よりも、グネグネ * 4 の方がいい気がする

*-* *-*-*-*-*  C-C C-D-D-D-D
| | |       |  | | |       |
* * * *-*-*-*  C C C D-D-D-D
| | | |        | | | |      
* * * *-*-*-*  C C C D-D-D-D
| | |          | | |        
* *-* *-*-*-*  C C-C @-A-A-A
|           |  |           |
*-*-*-* *-* *  B-B-B-B A-A A
      | | | |        | | | |
*-*-*-* * * *  B-B-B-B A A A
|       | | |  |       | | |
*-*-*-*-* *-*  B-B-B-B-A A-A

  1. 渦巻きは順並行、グネグネは逆平行が初期状態に多い。
    => そもそも double bridge が有効なら逆平行が多い方が気がする

  2. グネグネは局所的な改善が多く見込めそう
    => 渦巻きは渦の中心付近の 2opt 操作では大きく状態を壊さないが、 外側の操作は大きく状態を壊しやすい
    一方グネグネは上図右の同一アルファベットのみを操作する場合、その他のアルファベットへの影響は皆無。 A区間のみを改善する、みたいな操作が可能
    A,B,C,D をそれぞれ独立に改善し、 後で全体を改善する操作が出来そう
    局所的な改善は差分計算も高速。 1遷移 O(N^2) だとすると 1/4 になる

焼き鈍しのスコア関数がムズイ……

  • Nが小さい => 割とランダムに動かしてもいい (温度高めがいい)
  • Nが大きい => そもそも山登りでも十分なくらい空間が大きい (温度低めが良い)
  • Vが小さい => 状態はなだらか。 スコア差が小さい (温度低めが良い？)
  • Vが大きい => 状態は凸凹。 スコア差が大きい (温度高めが良い？)

(N, V) の組でいくつかサンプル取ってケース毎に決める…？

diff = rawScore diff
T(N, V) = ?

V の値によって適当な定数を加算して比率を取る？

{(s1 + const) - (s0 + const)} / (base score + const)
  1. {A,B,C,D} 独立に改善
  2. {AB, BC, CD} 独立に改善
  3. ABCD 全体を改善

のような流れになる。

局所改善のとき、 大きい数を中央に寄せる方がいい？

とりあえず今のやつを初期解と比較。
200 ケースで平均 3.81 倍のスコア -> 順位表で言うと 0.85 - 0.95 あたり？ まだ雑な奴だから偏ってる可能性も (順位表側が)
1000 ケース 3.74 倍。 結構ぶれる
時間いっぱいまでやるやつ ->

頑張って差分計算とかやるやつを実装。 つらい…。 それなりに速くなったかな？
端点moveで一回謎の落ち方をしたけど再現できない…。 適当に書き直したときに直った…？

アイデア

  1. (N, V) の組でパラメータ調整
  2. ブロックを段々に合わせて最適化
    (A -> B -> C -> D じゃなくて、 A -> AB -> ABC -> ABCD)
  3. スコアを以下のようにする 
    raw score + dist score
    大きな数が中心にくるほど良いイメージ。 中心付近は ABCD 2-4パートの境界に近いので 複数の部分から独立に集めやすい。
    このスコアを導入して自動で集まってくれることを期待

1 をとりあえず採用。 optuna で焼き鈍しのパラメータを調整。 もう残り12時間ぐらいしかないけど寝ながらでもおｋ
2 は微妙。 独立に動かしたままの方がスコアが微妙に高い 3 は独立に動かすパートのときのみ採用。 上手く合成するのが面倒だから.

時間がない

optuna で

  • 焼き鈍しの初期温度
  • 生スコアに掛ける係数
  • 試行回数によって温度を戻すイメージで itr % mod を採用してこの mod の値 を調整

寝てた。 あーさー

スコアは 4.8 倍平均とかになったけど、 score / max score で見てみると ベースライン(渦巻き) が 0.26 - 0.30 ぐらいにしかならない。
順位表のスコアと合わせると 0.985 / 0.30 * 0.245 = 0.80 とかにしかならない…。 ブレがあると下手すると 0.7 ぐらいにしかならないのでは…
焼き鈍しも全然収束してなくてダメそう…。 定数倍改善やだ

現状

  1. A,B,C,D を独立に焼き鈍し
  2. AB, CD を独立に焼き鈍し
  3. ABCD を焼き鈍し

で同じパラメータを使ってるけど、 1,2 に前項の距離スコアを導入して1,2用パラメータを導入。 がんばれ optuna

提出。 キューが詰まる

1,2 用のパラメータ調整が終わる。 εだけ良くなってそう。

待ってられないのでもう調整後のやつも提出。 キューに残ってると提出できない前システムだと死んでた

延長したらしい。 もう知らん。

最初の提出が 0.865 とかで返ってきたっぽい。 キューに入ってて順位表にいない人も多いから 0.85 ぐらいのスコアかな？
他の人のスコア見る限り 7-9 位ぐらいでしょうか。 上位赤+経験者しかいない。 強い…。

キューが捌けた。 最終提出は1投目よりちょい下がって 84.17083。 うーん？ まぁ 8 位で、上二人もシード次第で変わりそう

反省会

iehn さんの seed 1 、 5000 超とは…。(4000弱が最適解じゃないのか…) あー、空白アリのシステムかな。 小さい盤面だと結構差が付きそうだ…。
最初の頃には余った時間で尻尾削ってリトライとか考えてたんだけどなぁ。 完全に抜け落ちていた。
というか、 頭 - 尻尾の偽辺にブランクをいくつか追加するだけで良かったじゃん。 うへー。
wleite さんはブロックを区切るほうかぁ。 初期の盤面をもうちょい工夫して 4 パートじゃなくてもっと多くしてればよかったかな。
こっちは単純に時間が足りなかった感。
ていうか皆盤面埋めてないのか。 マジか。
焼き鈍しも2倍ぐらい高速化できたらスコアもうちょい安定すると思うんだけど…。 焼きなまし空間ガタガタ過ぎる (下手っぴ)

今回は実験用にコード書いてから全部投げ捨てて綺麗に実装し直すというマラソンぽいことをしたけどやっぱり1週間だとつらいぜ。。。
おしまい

@koyumeishi
Copy link
Author

double bridge

Sign up for free to join this conversation on GitHub. Already have an account? Sign in to comment