A recursive solution to the towers of hanoi problem in C++ using built in stack

towers_of_hanoi.cpp

#include <bits/stdc++.h>

using namespace std;

void pegPrint(stack<int> peg,char x)
{
    cout<<"**********  "<<x<<"  ************"<<endl;
    for(; peg.empty() != true; peg.pop())
    {
        cout<<"-  ";
        for(int i=0; i<peg.top(); i++)
        {
            cout<<"O";
        }
        cout<<"  -"<<endl;
    }
    cout<<"***************************"<<endl<<endl;
}


void moveStack(stack<int> &src, stack<int> &dest)
{
    dest.push(src.top());
    src.pop();
}

void hanoi(int n, stack<int> &A,stack<int> &B, stack<int> &C)
{
    //uncomment these to see each step
    // cout<<n<<endl;
    // pegPrint(A,'A');
    // pegPrint(B,'B');
    // pegPrint(C,'C');

    if(n==1)
    {
        moveStack(A,C);
        return;
    }

    hanoi(n-1,A,C,B);
    moveStack(A,C);
    hanoi(n-1,B,A,C);
    return;
}



int main()
{
    stack<int> A,B,C;

    int n = 9;

    for(int i=n; i>0; i--)
    {
        A.push(i);
    }

    pegPrint(A,'A');
    pegPrint(B,'B');
    pegPrint(C,'C');

    hanoi(n,A,B,C);

    pegPrint(A,'A');
    pegPrint(B,'B');
    pegPrint(C,'C');

    return 0;
}

This is a very helpful tree diagram for understanding the underlying logic of the recursive algorithm.
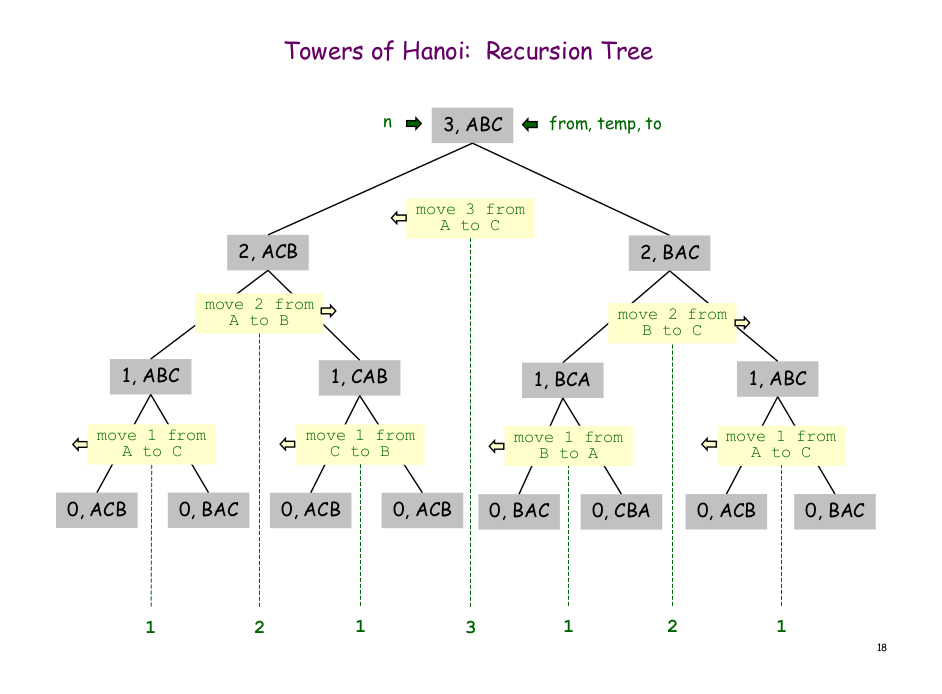
This shows the approach for n = 3