Skip to content

Instantly share code, notes, and snippets.

@Fingercomp

Fingercomp/sound-card-guide-3.markdown Secret

Last active September 27, 2017 00:51
Show Gist options
  • Star 0 You must be signed in to star a gist
  • Fork 0 You must be signed in to fork a gist
  • Save Fingercomp/3951275887c3d78df88c93ef9e818a20 to your computer and use it in GitHub Desktop.
Save Fingercomp/3951275887c3d78df88c93ef9e818a20 to your computer and use it in GitHub Desktop.
Download ZIP
Sound Card / спектр, преобразование Фурье, форматы PCM и WAV
Raw
sound-card-guide-3.markdown

Содержание

Функция синусоиды

Что такое синусоида? Я в обоих частях употреблял это слово, но ответа на такой вопрос я не давал. Пофиксим-с.

Итак, синусоида - это просто график вот такой функции.

  • - время, с.
  • - амплитуда.
  • - частота, Гц.
  • - угловая частота, рад; указывает, на сколько радиан изменяется значение функции в секунду.
  • - фаза колебаний, сдвигает функцию по горизонтали: вперёд при положительных значениях, назад при отрицательных.

У синусоиды есть очень интересная особенность. Если двигаться по кругу радиуса с угловой частотой и в каждый момент времени на графике рисовать положение относительно какой-либо оси, то получим синусоиду.

И это не всё. Выразим через косинус:

,

.

Интересовать во втором выражении должно только то, что амплитуду с фазой можно представить как комплексное число (это число называется комплексной амплитудой), при этом , . Мы будем использовать комплексную амплитуду в последующих главах.

Аддитивный синтез звука

Синусоиды - это, конечно, замечательно, но в реальной жизни звуковые колебания имеют более сложную форму. Одним из известных способов генерации звука является аддитивный синтез. В чём суть: есть энное число синусоид (или других периодических волн, но мы будем юзать именно синусоиды), в каждый момент времени получаются их текущие значения и складываются. Иными словами,

, где

  • - количество составляющих синусоид;
  • - амплитуда k-ой синусоиды;
  • - частота k-ой синусоиды;
  • - начальная фаза k-ой синусоиды.

Говорю я про это не случайно: все каналы звуковой карты складываются, то есть там применяется аддитивный синтез.

Временная и частотная области

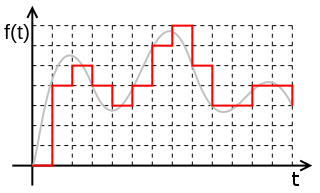
Как выглядят несколько синусоид, сложенных вместе? Возьмём 6 синусоид. Частоту и амплитуду первой примем за и . Для остальных частота , а амплитуда , где - это первые 6 нечётных чисел (1, 3, 5, 7, 9, 11). И сложим!

По горизонтали время (единица измерения: 1/16384 секунд), по вертикали амплитуда. Это график временной области сигнала. То есть здесь показывается зависимость амплитуды от времени. Очевидно, что если ввели такой странный термин, как временная область, должна быть ещё какая-то. Оказывается, есть ещё частотная область сигнала: это уже анализ зависимости амплитуды от частоты, что логично.

По горизонтали частота в герцах (интервал в 1 Гц), по вертикали - амплитуда синусоиды данной частоты. Это как нажатые клавиши фортепиано в данный момент времени. Частотная область звуковой волны называется её спектром. Непривычно? О том, зачем нужна такая необычная штука, будет рассказано в следующих главах.

Обработка звука: дискретизация и квантование

Мне кажется очевидным (и вам должно), что звук непрерывен, не дискретен. То есть значение функции, задающую звуковую волну, меняется не резко (то есть имеется, например, ноль, потом сразу единица, а промежуточных значений нет, как в таких часах, где секундная стрелка перемещается на ровно 1/60 часть окружности каждую секунду), а плавно переходит из одного значения в другое. Когда мы хотим сохранить звук, нам приходится иметь дело с ограниченной точностью и переводить непрерывную функцию в дискретную, измеряя значение функции через равные интервалы времени. Почему это печально? Согласно теореме Котельникова, этот интервал времени , где - максимальная частота спектра волны. Если интервал больше, то слишком быстрые слагающие сигнал частоты не могут быть корректно восстановлены назад при воспроизведении. Получение значений функции через равные интервалы времени называется дискретизацией функции: превращении её в дискретную. А сам интервал (точнее, частота измерения ) - частотой дискретизации.

Итак, мы получили амплитуды в виде дробных чисел через равные интервалы. Думаете, на этом печалька закончилась? Ха-ха, нет. Дробные-то числа тоже требуют бесконечной точности для точного восстановления. А память не резиновая. Облом.

Поэтому значения амплитуды делятся на некоторые интервалы. Такое разбиение амплитуды на интервалы назвается квантованием.

Обозначив максимальную амплитуду за 32767, например, а минимальную за -32768, мы получаем 65536 интервалов амплитуды. Количество интервалов в битах называется глубиной дискретизации. В этом случае глубина дискретизации равна 16 бит.

Квантованный сигнал; сигнал с дискретным временем; квантованный сигнал с дискретным времением (цифровой).

Преобразование Фурье, дискретное преобразование Фурье

Наконец-то мы дошли до самых весёлых частей этой статьи. Вы наверняка подумали в предыдущей части, а как же получить спектр звуковой волны, если у нас известна только её временная область?

Умный дядя Фурье сказал и доказал, что любую звуковую волну можно разложить на бесконечное число синусоид.

Отлично. Но есть несколько мелочей:

  • Количество синусоид бесконечно (мало того, что тут интеграл, так ведь ещё и от до ).
  • Исходный сигнал должен быть периодическим (то есть повторяться через некоторый промежуток времени).
  • Исходный сигнал должен быть так же бесконечно долгий.
  • Исходный сигнал должен быть непрерывным.

Начать хотя бы с того, что у нас музяка длится конечное время, а перед сохранением она прошла дискретизацию и квантование. Так что эта страшная штука нам в чистом виде не нужна.

Поэтому существует дискретное преобразование Фурье (ДПФ, DFT).

, где

  • - количество измеренных значений сигнала (обзовём их сэмплами);
  • - порядковый номер синусоиды, от 0 до ;
  • - комплексная амплитуда k-ой синусоиды;
  • - амплитуда синусоиды ;
  • - фаза синусоиды ;

Частота синусоиды , где - период времени, в течение которого измерялась функция. , - частота дискретизации.

Здесь, вообще, тоже надо бы давать периодический сигнал. Но кому до этого есть дело, верно? Поэтому можно просто скормить небольшой кусок всего измеренного сигнала (например, 1024 измерений). Такой кусок называется окном. Чем больше , тем точнее высчитывается частота. Однако увеличивается погрешность во времени. И наоборот: если взять меньше, то мы увеличиваем точность во времени, но получаем погрешность в частоте.

Математика ДПФ очень простая, поэтому я приведу функцию (на луа, естественно), которая для таблицы значений samples вернёт спектр. Я использую библиотеку комплексных чисел complex на LuaUsers, чтобы не отвлекаться на всякие базовые формулы, касающиеся этих чисел, и показать сам алгоритм.

local function dft(samples)
  local N = #samples
  local result = {}
  for k = 1, N, 1 do
    local sum = 0
    for n = 1, N, 1 do
      sum = sum + samples[n] * (complex {0, -(2 * math.pi / N) * (k - 1) * (n - 1)}):exp()
    end
    result[k] = sum
  end
end

local function decomposeComplexAmplitude(fourier, sampleRate)
  for k, v in pairs(fourier) do
    local frequency = (k - 1) / (#fourier / sampleRate)
    local amplitude = v:abs() / #fourier
    -- Фаза для косинуса, поэтому прибавляем π/2 и закругляем вокруг
    -- круга (2π)
    local phase = (select(2, v:polar()) + math.pi / 2) % (2 * math.pi)
    fourier[k] = {frequency, amplitude, phase}
  end
end

dft - само ДПФ, а decomposeComplexAmplitude комплексные числа переводит в тройку: частота, амплитуда и начальная фаза.

Ну всё, теперь мы точно тузика порвём. Мы же можем переводить из временной области в частотную! Но если запустим эту функцию, передав буквально пару тысяч сэмплов, то ждать нам придётся... мм, довольно долго. Нерасторопный алгоритм этот. Попробуйте забить таблицу 10'000 единицами и скормить это ДПФ, если интересна скорость.

Быстрое преобразование Фурье

И поэтому сама собою напрашивается глава о вариации дискретного преобразования Фурье, которая будет, ну, скажем так, пошустрее.

Давайте посмотрим ещё раз на алгоритм ДПФ. У нас есть цикл с N шагов, в котором есть ещё один цикл, тоже с энным числом шагов, и в итоге мы проходимся по циклу раз. Это означает, что сложность алгоритма - . Для 10'000 единиц мы проходимся по массиву аж 100'000'000 (100 миллионов) раз! Ну ни в какие ворота не лезет.

Поэтому существуют алгоритмы быстрого преобразования Фурье. Фишка их в том, что они позволяют уменьшить сложность до . Долго расписывать, как работают такие алгоритмы, я тут не буду, потому что это не самая простая для усвоения тема. Сразу перейдём к наиболее распространённому алгоритму Кули-Тьюки.

Алгоритм заключается в том, что мы последовательно и неотвратимо делим все переданные функции сэмплы на две части: те, что на чётных позициях, и те, что на нечётных. Затем для каждой из этих частей снова вызываем ту же функцию, т.е. рекурсивно. В конце концов мы дойдём до варианта, при котором у функции будет два значения, и нужно будет просто вернуть их сумму и разность. Затем домножаем элементы массива нечётных значений на некоторое комплексное число и складываем, а потом снова идём вверх по стэку.

Это всё неинтересно, кроме одной детали. Мы делим на 2 постоянно, поэтому число значений должно быть степенью двойки. 2, 4, 8, 16, 32, 64 и т.д. Я использую 1024 сэмпла - устраивает по точности как во времени, так и в частоте (если сэмплрейт больше 44 кГц).

Мы программируем не на Хаскелле. Рекурсия у нас - штука дорогая, жрёт память почём зря. Поэтому существует модификация алгоритма, которая не создаёт лишних массивов (работает с одним) и не использует рекурсию.

local function reverseBits(num, bitlen)
  local result = 0
  local n = 1 << bitlen
  local nrev = num
  for i = 1, bitlen - 1, 1 do
    num = num >> 1
    nrev = nrev << 1
    nrev = nrev | (num & 1)
  end
  nrev = nrev & (n - 1)
  return nrev
end

local function fft(x)
  local bitlen = math.ceil(math.log(#x + 1, 2))
  local data = {}
  for i = 0, #x, 1 do
    data[reverseBits(i, bitlen)] = complex(x*)
  end
  for s = 1, bitlen, 1 do
    local m = 2^s
    local hm = m * 0.5
    local omegaM = (complex {0, -2 * math.pi / m}):exp()
    for k = 0, #x, m do
      local omega = complex(1)
      for j = 0, hm - 1 do
        local t = omega * data[k + j + hm]
        local u = data[k + j]
        data[k + j] = u + t
        data[k + j + hm] = u - t
        omega = omega * omegaM
      end
    end
  end
  return data
end

Есть забавная функция reverseBits: она из числа типа (b - это двоичные цифры) делает . Кроме того, входной массив для fft должен начинаться с нуля, а его длина (точнее, выхлоп #x) на единицу должна быть меньше количества сэмплов. Возвращаемое значение тоже начинается с нуля. Из БПФ данные дальше перегоняются в тот же распаковщик и затем используются.

Форматы аудио без компрессии: PCM, WAV

В чём сохранять звук? У нас есть два варианта: выбрать какой-нибудь кодек, который оптимизирует размер файла, или же тупо сохранять данные как есть, никак их не обрабатывая. Выберем второй вариант.

PCM (а, точнее, LPCM, который мы будем рассматривать) - это такой забавный формат. В нём данные о звуке хранятся так:

  • Весь файл - это последовательность структур моментов времени, в которых хранятся все сэмплы звуковых волн в данный момент времени. При проигрывании они считываются и содержимое играется ровно 1/sample_rate секунд. Таким образом, количество таких структур за одну секунду аудио в файле PCM равно частоте дискретизации.
  • Структура момента времени состоит из последовательности каналов: 1 канал - это моно, 2 канала - стерео.
  • Каждый канал состоит из одного сэмпла - измеренного значения звуковой волны.
  • Каждый сэмпл состоит из некоторого количества байтов, равного глубине дискретизации, делённой на 8.

В итоге в файл приходит жить последовательность байтов.

Итоговый размер файла получается равен времени в секундах, умноженому на сэмплрейт, умноженный на количество каналов, умноженное на глубину дискретизации, делённой на 8.

Проблема с сырым PCM в том, что при проигрывании приходится вручную указывать его параметры. Поэтому для хранения необработанных звуковых данных лучше использовать формат WAV. По сути, это всего 44 байта хедеров, после которых идёт PCM. Формат хедеров следующий:

  • 01-04 [BE 4] Строка "RIFF"
  • 05-08 [LE 4] Размер файла, уменьшенный на 8 байтов
  • 09-12 [BE 4] Строка "WAVE"
  • 13-16 [BE 4] Строка "fmt "
  • 17-20 [LE 4] Число 16
  • 21-22 [LE 2] Число 1
  • 23-24 [LE 2] Число каналов
  • 25-28 [LE 4] Частота дискретизации
  • 29-32 [LE 4] Частота дискретизации, умноженная на кол-во каналов, умноженное на глубину дискетизации, делённую на 8.
  • 33-34 [LE 2] Глубина дискретизации, делённая на 8 и умноженная на кол-во каналов.
  • 35-36 [LE 2] Глубина дискретизации
  • 37-40 [BE 4] Строка "data"
  • 41-44 [LE 4] Размер звуковых данных
  • 45-... [LE] Звуковые данные

BE - это Big-Endian, то есть старшие байты идут первыми (0x123456 кодируется как \x12\x34\x56); LE - Little-Endian, старшие байты идут последними (0x123456 кодируется как \x56\x34\x12). Слева позиция в файле, справа размер значения в байтах.

Проигрыватель PCM для OpenComputers

В теории, теперь есть вся информация о том, как проигрывать PCM или WAV на OpenComputers. Алгоритм следующий:

  • читаем 1024 сэмплов;
  • прогоняем через БПФ;
  • выбираем самые громкие составляющие (то есть синусоиды, амплитуды которых наибольшие);
  • устанавливаем настройки каналов, соответствующие параметрам синусоид;
  • воспроизводим.

И так повторять до конца файла. Ничего сложного, на самом деле. Единственная проблема - нельзя указать фазу. Каналы могут быть рассинхронизованы. Но сильно на звуке это сказываться не должно: тут больше проблем доставляет небольшое количество каналов. Ещё есть проблема с тормозными серверами: пинг до сервера должен быть минимальный, а соединение - отличным.

Я пилю такой проигрыватель: прогресс на моей репе. Напишу отдельно, когда посчитаю более-менее законченным. А пока можно просмотреть код и сопоставить с информацией из этой статейки.

Это был краткий гайд по проигрыванию звука посложнее пары синусоид. Считаю, что теперь с туториалом по звуковой карте и по звуку в целом я, наконец, закончил. Теперь можно спокойно играться со звуковой картой и самостоятельно пилить программы, которые будут её использовать.

Have fun!

Sign up for free to join this conversation on GitHub. Already have an account? Sign in to comment