数据结构(英语:data structure)是计算机中存储、组织数据的方式。——维基百科
- 数组(Array)
- 栈(Stack)
- 队列(Queue)
- 链表(Linked List)
- 集合(Set)
- 散列表(Hash) 和 字典(Map)
- 树(Tree)
- 图(Grapj)
在 js 里数组是一个最常用的数据类型之一,创建一个数组有很多方法,最常用的就是直接定义一个空数组:
var arr = []
在 js 里数组有很多操作方法,比如:push, pop, unshift, shift, splice, map, reducer, every等等等等,具体 的可以参考 MDN:https://developer.mozilla.org/zh-CN/docs/Web/JavaScript/Reference/Global_Objects/Array
遵守后进先出原则的有序集合
实现一个栈很简单,比如我们把所有元素存在一个叫 arr 的数组里,然后通过数组的 push, pop 方法就可以实现一个基本的栈了。
var arr = [];
arr.push(1,2,3)
arr.pop()
console.log(arr) // [1,2]遵守先进先出原则的一组有序项
实现一个队列同样很简单,像栈一样定义一个数组 arr 存放队列的元素,然后通过数组的 shift, unshift 方法来实现一个 基本的队列
var arr = [];
arr.unshift(1,2,3)
arr.shift()
console.log(arr) // [1,2]js 里数组自带 sort 排序方法,不过它的具体实现算法根据浏览器的引擎不同在每个浏览器上实现可能都不一样,下面介绍最常见的排序算法 怎么用 js 实现
function swap(arr, index1, index2) {
var aux = arr[index1]
arr[index1] = arr[index2]
arr[index2] = aux
}
function bubbleSort(arr) {
var len = arr.length;
for (var i = 0; i < len; i++) {
for (var j = 0; j < len - i - 1 ; j++) {
if (arr[j] > arr[j+1]) {
swap(arr , j ,j+1)
}
}
}
return arr
}
// 测试
var a = bubbleSort([5,4,3,2,7,1]); // a = [1,2,3,4,5,7]function swap(arr, index1, index2) {
var aux = arr[index1]
arr[index1] = arr[index2]
arr[index2] = aux
}
function selectorSort(arr) {
var len = arr.length,indexMin;
for (var i = 0; i < len -1 ; i++) {
indexMin = i;
for (var j = i ; j < len; j++) {
if (arr[indexMin] > arr[j]) {
indexMin = j
}
}
if (i !== indexMin) {
swap(arr ,i, indexMin)
}
}
return arr
}
// 测试
var a = selectorSort([5,4,3,2,7,1]); // a = [1,2,3,4,5,7]function insertSort(arr) {
var len = arr.length,j ,temp;
for (var i = 1; i < len; i++) {
j = i;
temp = arr[i];
while (j > 0 && arr[j-1] > temp) {
arr[j] = arr[j-1]
j--;
}
arr[j] = temp
}
return arr
}4.归并排序:将原始数组切分成较小的数组,直到每个小数组只有一个位置,接着将小数组归并成较大数组,直到最后只有一个排序完成的大数组。归并排序是一种分治思想, firefox 浏览器对于 js 数组原生的 sort 方法实现就是用的归并算法
function merge(left, right) {
var result = [], il = 0, ir = 0;
while(il < left.length && ir < right.length) {
if(left[il] < right[ir]) {
result.push(left[il++]);
} else {
result.push(right[ir++]);
}
}
while (il < left.length) {
result.push(left[il++])
}
while(ir < right.length) {
result.push(right[ir++])
}
return result;
}
function mergeSort(arr) {
var len = arr.length;
if (len === 1) {
return arr
}
var mid = Math.floor(len/2),
left = arr.slice(0, mid),
right = arr.slice(mid, len);
return merge(mergeSort(left), mergeSort(right));
}
// 测试
var a = selectorSort([5,4,3,2,7,1]); // a = [1,2,3,4,5,7]function quickSort(arr) {
quick(arr, 0, arr.length - 1)
return arr;
}
function quick(arr, left, right) {
var index;
if (arr.length > 1) {
index = partition(arr, left, right);
if (left < index - 1) {
quick(arr, left ,index - 1)
}
if (index < right) {
quick(arr, index, right)
}
}
}
function swap(arr, index1, index2) {
var aux = arr[index1]
arr[index1] = arr[index2]
arr[index2] = aux
}
function partition(arr, left, right) {
var pivot = arr[Math.floor((right + left) / 2)], i = left, j = right;
while(i <= j) {
while(arr[i] < pivot) {
i++
}
while(arr[j] > pivot) {
j--
}
if (i <= j) {
swap(arr, i ,j)
i++;
j--;
}
}
return i
}
// 测试
var a = selectorSort([5,4,3,2,7,1]); // a = [1,2,3,4,5,7]大 O 表示法通常来描述算法的性能和复杂程度。一般讨论的是 CPU 占用时间
- O(1) 常数的
- O(log(n)) 对数的
- O(log(n)c) 对数多项式的
- O(n) 线性的
- O(n^2) 二次的
- O(n^c) 多项式的
- O(c^n) 指数的
O(1)
function add(n) {
return ++n
}
O(n)
function search(arr, item) {
for (var i = 0; i < arr.length; i++) {
if (item === arr[i]) {
return i
}
}
return -1
}
如果数组arr 的长度为 n,那么这个函数的时间复杂度就是 O(n)
O(n^2)
function swap(arr, index1, index2) {
var aux = arr[index1]
arr[index1] = arr[index2]
arr[index2] = aux
}
function bubbleSort(arr) {
var length = arr.length;
for (var i = 0; i < length; i++) {
for (var j = 0; j < length -1; j++) {
if (arr[j] > arr[j+1]) {
swap(arr, j, j+1)
}
}
}
}
上面这个类似冒泡排序的函数,有两层循环,如果数组的长度为 n;那么时间复杂度应该为 O(n^2)
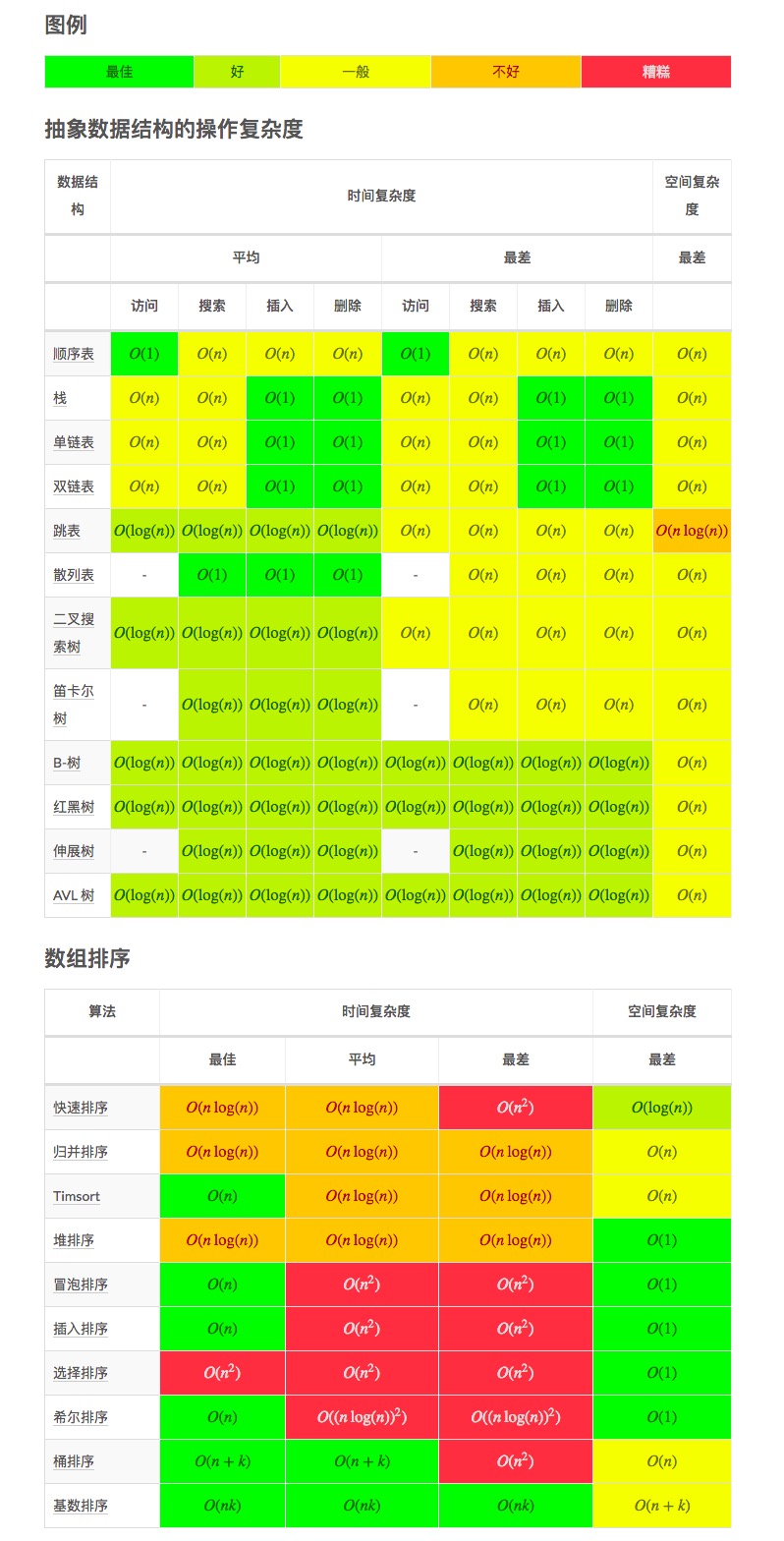
下面这两张图是之前在某个网站上面看到的,但是因为那个网站用的是文字写的,我当时为了记录方便直接截图保存在印象笔记了,所以暂时找不到原文作者了,如果作者看到请联系我添加原文链接