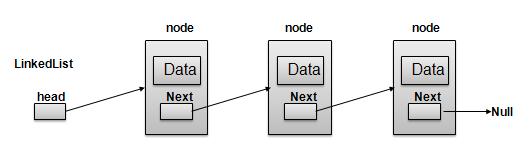
Linked lists are a way to store sequential data. A linked list is made up of one or more list nodes that contain the data and a link or pointer to the next node in the sequence. We call the start of the linked list the head and the end of the linked list the tail.
Image from: https://www.tutorialspoint.com/data_structures_algorithms/linked_lists_algorithm.htm
- Constant time insertions/deletions
- Easily expandable
Let’s think about how data is stored on our computers. When using an array the items in our array are stored one after another in memory in contiguous blocks something like this:
| Register | Stored Data | Register | Stored Data | |
|---|---|---|---|---|
| Loc # 608 | “Chicago” | Loc # 608 | “Atlanta” | |
| Loc # 609 | “Columbus” | Loc # 609 | “Chicago” | |
| Loc # 610 | “Denver” | Loc # 610 | “Columbus” | |
| Loc # 611 | “Kansas City” | Loc # 611 | “Denver” | |
| Loc # 612 | “New York” | Loc # 612 | “Kansas City” | |
| Loc # 613 | Loc # 613 | “New York” |
Here we have an array with 5 items with space for 1 additional item. Array[0] is “Chicago” and array[4] is “New York”. Great! But what happens if we wanted to add “Atlanta” to the first spot in our list? Each item in our array would need to be shifted one spot down to make room for “Atlanta” and that could take a while if we had a really big array.
Linked lists aren’t stored in contiguous blocks of memory, so when a node is added to the list the location of the other nodes isn’t affected. To add a node we just need to update a link or two, and this can be done with the same number of steps each time. For example:
Image from: https://www.tutorialspoint.com/data_structures_algorithms/linked_lists_algorithm.htm
If you’re familiar with big O notation, we’d say that removing or inserting a value at the front of an array is O(n). For a linked list though removing or inserting a value at the front of the list is O(1), or constant time. For some applications this could be very useful!
Let’s think back to our previous array. It was only allocated 6 blocks in memory. What happens if we wanted to add “Los Angeles” to it?
| Register | Stored Data |
|---|---|
| Loc # 608 | “Atlanta” |
| Loc # 609 | “Chicago” |
| Loc # 610 | “Columbus” |
| Loc # 611 | “Denver” |
| Loc # 612 | “Kansas City” |
| Loc # 613 | “New York” |
Since the array is full, the system would need to find a new location for a bigger array, copy over all the items in the array, and then add the new item. With a linked list though, we’d just have to add another node - since it doesn’t need contiguous blocks of memory it’s very flexible.
Linked lists aren’t as easy to navigate. Arrays have a special property - you can access any item in the linked list in constant time. If we wanted the second item in our array we could use array[1]. But with linked lists we have to start at the head node and follow the next links until we get to the item we want. For example:
Image from: https://www.tutorialspoint.com/data_structures_algorithms/linked_lists_algorithm.htm
In big O notation we’d say an array has O(1) or constant time access, but linked lists have O(n) access because we may need to traverse every node in the linked list to get to the node we want.
Three common types:
- Singly linked lists (this is what we’ve been using!)
- Doubly linked lists - has link to the next node AND the previous node
- Circular linked lists - the next value of the last node is the head
Here is a definition for a list node and a linked list in Python.
class ListNode:
def __init__(self, val=None):
self.data = val
self.next = None
class LinkedList:
def __init__(self):
self.head = None
def setHead(self, head):
self.head = headWe can create the head of our list like this:
my_list = LinkedList()
node = ListNode(10)
my_list.setHead(node)Let’s create a method to insert a node at the end of a Linked List!
def insertAtEnd(self, data):
node = ListNode(data)
if self.head is None:
self.setHead(node)
else:
curr = self.head
while curr.next is not None:
curr = curr.next
curr.next = nodeGiven a Singly Linked-List, check whether its length is even or odd.
Example:
1->2->3->4 ==> True
1->2->3->4->5 ==> False
Hint # 1: Traversing over the linked list with 2x the speed (over two nodes at a time) in a loop can give you an interesting and efficient solution in a single pass.
Hint # 2:
- Traverse over the
Linked Listby hopping over twoNodesat a time. - While traversing, keep a check to exit out of the loop if the
nextreference of thecurrent NodebecomesNone. - If the
current NodebecomesNoneat the end of the traversal, the length is even - otherwise it's odd.
def is_list_even(self):
if self.head:
n = self.head
c = 1
while n.next:
n = n.next
c += 1
return c % 2 == 0
return True
OR: def is_list_even(self):
current = self.head
while current is not None:
if current.next is not None:
current = current.next.next
else:
break
if current is None:
return True
else:
return FalseGiven a singly linked list, write a method to perform In-place reversal.
Example:
1->2->3 ==> 3->2->1
Hint # 1: The key here is to reverse the next link to the previous node at each step of the traversal till you reach the end of the list.
Hint # 2:
- Create a node -
lastand initialize it toNone. - Start traversing through the list by marking
head nodeas the current node, till you reach to the end of thelist. - Within the loop, create a temporary variable next to store the current's next node.
- Point the next link of the current node to the
lastnode, created in step one. - Set
last = currentandcurrent = next. - At the end of the loop, set
head = last, which results in the head pointing to the reversed list.
def reverse(self):
prev = None
curr = self.head
while curr is not None:
temp = curr.next
curr.next = prev
prev = curr
curr = temp
self.setHead(prev)Given a Singly Linked-List, implement a method to delete the node that contains the same data as the input data.
Hint # 1: Traverse over to the position with the same data as the input. Use a temporary variable to hold the previous node and point its next reference to the next reference of the current node.
Hint # 2:
- Traverse to the required
Nodein thelist, keeping track of the previous and current nodes. - Set the previous node's next pointer to
current.next. - Set
current.nextto None.
Example:
delete(1->2->3->4,3) ==> 1->2->4
def delete(self,data):
if self.head is None:
return None
if self.head.data == data:
self.setHead(self.head.next)
return self.head
n = self.head
while n.next.data != data:
n = n.next
if not n: return self.head
n.next = n.next.next
return self.headGiven a Singly Linked-List, write a function that returns the "Nth from the end" node of the list.
Example:
1->2->3->4->5->6, n=2 ==> 5
Your solution should return the entire node, not just it's data.
Hint # 1:
The problem can be solved by traversing the Linked List twice, one for finding the length and the other to return the position of the node.
Hint # 2:
We can get the position of the Nth Node from the end with the formula: 'length-n+1'.1. First find the length of the List. Traverse over the Linked List one more time to the Nth position and return the Node. 2. Since we didn't use extra memory, the runtime is O(n) and space complexity is O(1).
def find_nth_node_from_end(self, n):
count = 0
curr = self.head
while curr != None:
count += 1
curr = curr.next
curr = self.head
if count < n or n < 0:
return None
while count > n:
curr = curr.next
count -= 1
return currMerge two sorted linked lists and return it as a new list. The new list should be made by splicing together the nodes of the first two lists.
Example:
Input: 1->2->4, 1->3->4
Output: 1->1->2->3->4->4
def mergeTwoLists(self, list1, list2):
if list1 is None:
return list2
If list2 is None:
return list1
if list1.data < list2.data:
list3 = list1
node3 = list3
list1 = list1.next
else:
list3 = list2
node3 = list3
list2 = list2.next
while list1 is not None and list2 is not None:
if list1.data < list2.data:
node3.next = list1
node3 = node3.next
list1 = list1.next
else:
node3.next = list2
node3 = node3.next
list2 = list2.next
if list1:
node3.next = list1
if list2:
node3.next = list2
return list3Gist content by Mary Troiani for presentation she gave at the Algorithms and Technical Interview Study Group - Dec 13, 2017 meetup
This is a part of a series of presentations for Learn Teach Code - Algorithm Study Group