Defines STLC as the free CCC over the base type in Agda directly with HITs. Proves canonicity directly by induction.

freeCCC.agda

{-# OPTIONS --cubical --no-import-sorts --postfix-projections -W ignore #-}
module freeCCC where
open import Cubical.Foundations.Prelude
open import Cubical.Foundations.HLevels
open import Cubical.Foundations.Function
open import Cubical.Foundations.Isomorphism
open import Cubical.Data.Unit using (Unit; isPropUnit; isSetUnit)
open import Cubical.Data.Bool using (Bool; true; false; if_then_else_; isSetBool)
open import Cubical.Data.Sum using (_⊎_; inr; inl)
open import Cubical.Data.Sigma using (Σ; _×_; ΣPathP)
open import Cubical.Reflection.RecordEquiv

-- TODO more consistent naming and style
-- Maybe turn into a literate agda file

variable
  ℓ ℓ' ℓ'' : Level

module _ where
  private variable
    A B C : Type ℓ
  -- Some set theory, you can safely ignore this module
  _×ₛ_ : hSet ℓ → hSet ℓ' → hSet (ℓ-max ℓ ℓ')
  (A , isSetA) ×ₛ (B , isSetB) = A × B , isSet× isSetA isSetB
  _→ₛ_ : hSet ℓ → hSet ℓ' → hSet (ℓ-max ℓ ℓ')
  (A , _) →ₛ (B , isSetB) = (A → B) , isSet→ isSetB

  record Pullback {A : Type ℓ} {B : Type ℓ'} {C : Type ℓ''}
    (f : A → C) (g : B → C) : Type (ℓ-max ℓ (ℓ-max ℓ' ℓ'')) where
    field
      fstₚ : A
      sndₚ : B
      pathₚ : f fstₚ ≡ g sndₚ
  open Pullback public
  unquoteDecl IsoPullbackΣ = declareRecordIsoΣ IsoPullbackΣ (quote Pullback)

  isSetPullback : isSet A → isSet B → isGroupoid C
    → {f : A → C} {g : B → C}
    → isSet (Pullback f g)
  isSetPullback isSetA isSetB isGroupoidC
    = subst isSet (sym (isoToPath IsoPullbackΣ))
      (isSetΣ isSetA λ _ → isSetΣ isSetB λ _ → isGroupoidC _ _)

  Pullback≡ : {f : A → C} {g : B → C}
    → {P Q : Pullback f g}
    → (p : P .fstₚ ≡ Q .fstₚ)
    → (q : P .sndₚ ≡ Q .sndₚ)
    → Square (P .pathₚ) (Q .pathₚ) (cong f p) (cong g q)
    → P ≡ Q
  Pullback≡ {P = P} p q r i = record {
      fstₚ = p i ;
      sndₚ = q i ;
      pathₚ = r i
      --  g(P.snd)-g(q i)-g(Q.snd)
      --     |               |
      --  P .pathₚ        Q .pathₚ    ↑ʲ
      --     |               |         ->ᵢ
      --  f(P.fst)-f(p i)-f(Q.fst)
    }

  isSet→Square : isSet A
    → {a₀₀ a₀₁ : A} (a₀₋ : a₀₀ ≡ a₀₁)
    → {a₁₀ a₁₁ : A} (a₁₋ : a₁₀ ≡ a₁₁)
    → (a₋₀ : a₀₀ ≡ a₁₀) (a₋₁ : a₀₁ ≡ a₁₁)
    → Square a₀₋ a₁₋ a₋₀ a₋₁
  isSet→Square isSetA = isSet→SquareP (λ _ _ → isSetA)

infixl 13 _×̇_  -- Added a dot to avoid clashing with _×_
infixr 12 _⇒_  -- The objects are generated by products and functions.
data Obj : Type where
  𝟙 Ans : Obj
  _×̇_ : Obj → Obj → Obj
  _⇒_ : Obj → Obj → Obj

data Hom : Obj → Obj → Type
variable
  A B C D : Obj
  f g h : Hom A B

infixl 20 _*_  -- Composition of morphism
data Hom where
  isSetHom : isSet (Hom A B)
  -- ^ This ensures the overall result is a set.
  -- Otherwise it would not be a category but a higher category, which
  -- would then require even more coherence laws.
  -- We could insist that isomorphic objects are equal in this category,
  -- but it is unnecessary for our purposes.

  _*_ : Hom B C → Hom A B → Hom A C
  ι : Hom A A
  idₗ : ι * f ≡ f
  idᵣ : f * ι ≡ f
  assoc : (f * g) * h ≡ f * (g * h)

  -- There is a terminal object.
  𝟙 : Hom A 𝟙
  η₁ : (p : Hom A 𝟙) → 𝟙 ≡ p

  -- We freely throw in a type with two closed elements.
  -- But note that we do not 𝑎 𝑝𝑟𝑖𝑜𝑟𝑖 know that yes ≠ no,
  -- or that Hom 𝟙 Ans only consists of yes and no.
  yes no : Hom 𝟙 Ans

  -- The products.
  π₁ : Hom (A ×̇ B) A
  π₂ : Hom (A ×̇ B) B
  ⟨_,_⟩ : Hom C A → Hom C B → Hom C (A ×̇ B)
  β₁× : π₁ * ⟨ f , g ⟩ ≡ f
  β₂× : π₂ * ⟨ f , g ⟩ ≡ g
  η× : ⟨ π₁ * f , π₂ * f ⟩ ≡ f

  -- The exponentials.
  ε : Hom ((A ⇒ B) ×̇ A) B
  ƛ : Hom (A ×̇ B) C → Hom A (B ⇒ C)
  β⇒ : ε * ⟨ ƛ f * π₁ , π₂ ⟩ ≡ f
  η⇒ : ƛ (ε * ⟨ g * π₁ , π₂ ⟩) ≡ g

-- Some properties of the calculus.
-- These are all required by Agda during the proof.
-- Not planned ahead.

-- Note that these are all just simply generated by terms of the language.
-- This means that they do not rely on the fact that Obj and Hom are freely
-- generated (to use this fact, we need to do induction). Thus, they would
-- hold in every model. We simply need to interpret these equations into
-- the models using ⦅_⦆ below, and cubical Agda will automatically compute
-- everything.
isContrHom-𝟙 : isContr (Hom A 𝟙)
isContrHom-𝟙 = 𝟙 , η₁

isPropHom-𝟙 : isProp (Hom A 𝟙)
isPropHom-𝟙 = isContr→isProp isContrHom-𝟙

⟨⟩-*-distr : ⟨ f , g ⟩ * h ≡ ⟨ f * h , g * h ⟩
⟨⟩-*-distr {f = f} {g = g} {h = h}
  = sym η×
  ∙ cong₂ ⟨_,_⟩
    (sym assoc ∙ cong (_* h) β₁×)
    (sym assoc ∙ cong (_* h) β₂×)

⟨π₁,π₂⟩ : ⟨ π₁ , π₂ ⟩ ≡ ι {A ×̇ B}
⟨π₁,π₂⟩ = sym idᵣ ∙ ⟨⟩-*-distr ∙ η×

-- I ran out of good names..
Lemma₁ : ⟨ f * g , h ⟩ ≡ ⟨ f * π₁ , π₂ ⟩ * ⟨ g , h ⟩
Lemma₁ {f = f} = cong₂ ⟨_,_⟩
  (cong (f *_) (sym β₁×) ∙ sym assoc) (sym β₂×)
  ∙ sym ⟨⟩-*-distr

Lemma₂ : ε * ⟨ ƛ f * g , h ⟩ ≡ f * ⟨ g , h ⟩
Lemma₂ {f = f} {g = g} {h = h}
  = cong (ε *_) Lemma₁ ∙ sym assoc ∙ cong (_* ⟨ g , h ⟩) β⇒

-- First a model to prove yes ≠ no. In cubical Agda, we need to do a little bit
-- more to prove that the interpretation of types are sets.
module SetModel where
  ⟦_⟧ : Obj → hSet ℓ-zero  -- The interpretation of objects
  ⟦ 𝟙 ⟧ = Unit , isSetUnit
  ⟦ Ans ⟧ = Bool , isSetBool
  ⟦ A ×̇ B ⟧ = ⟦ A ⟧ ×ₛ ⟦ B ⟧
  ⟦ A ⇒ B ⟧ = ⟦ A ⟧ →ₛ ⟦ B ⟧

  hom : hSet ℓ-zero → hSet ℓ-zero → Type  -- The interpretation of morphisms
  hom (A , _) (B , _) = A → B

  ⦅_⦆ : Hom A B → hom ⟦ A ⟧ ⟦ B ⟧  -- All obvious
  ⦅_⦆ {B = B} (isSetHom f g x y i j)
    = isSet→ (snd ⟦ B ⟧) ⦅ f ⦆ ⦅ g ⦆
      (cong ⦅_⦆ x) (cong ⦅_⦆ y) i j
  ⦅ f * g ⦆ = ⦅ f ⦆ ∘ ⦅ g ⦆
  ⦅ ι ⦆ = idfun _
  ⦅ idₗ {f = f} i ⦆ = ⦅ f ⦆
  ⦅ idᵣ {f = f} i ⦆ = ⦅ f ⦆
  ⦅ assoc {f = f} {g = g} {h = h} i ⦆ = ⦅ f ⦆ ∘ ⦅ g ⦆ ∘ ⦅ h ⦆
  ⦅ 𝟙 ⦆ _ = _
  ⦅ η₁ f i ⦆ _ = _
  ⦅ yes ⦆ _ = true
  ⦅ no ⦆ _ = false
  ⦅ π₁ ⦆ = fst
  ⦅ π₂ ⦆ = snd
  ⦅ ⟨ f , g ⟩ ⦆ u = ⦅ f ⦆ u , ⦅ g ⦆ u
  ⦅ β₁× {f = f} i ⦆ = ⦅ f ⦆
  ⦅ β₂× {g = g} i ⦆ = ⦅ g ⦆
  ⦅ η× {f = f} i ⦆ = ⦅ f ⦆
  ⦅ ƛ f ⦆ a b = ⦅ f ⦆ (a , b)
  ⦅ ε ⦆ (u , a) = u a
  ⦅ β⇒ {f = f} i ⦆ = ⦅ f ⦆
  ⦅ η⇒ {g = g} i ⦆ = ⦅ g ⦆

  -- See how cubical Agda handles the equations for us.
  yes≠no : yes ≡ no → true ≡ false
  yes≠no p i = ⦅ p i ⦆ _

module GlueModel where
  -- Now we prove canonicity, i.e. all the inhabitants of (Hom 𝟙 Ans) are equal
  -- to either yes or no. (The disjunction is constructive.)

  -- This time we interpret into a category 𝑜𝑣𝑒𝑟 (Obj,Hom).
  -- This means that the target category 𝓒 is indexed by (Obj,Hom).
  -- In traditional category theory, this is formalized by equipping 𝓒 with
  -- a functor 𝓒 → (Obj,Hom). So e.g. the preimage of (A : Obj) would be
  -- considered as "indexed" by A.

  -- However, in type theory we can do it much more concisely.
  Glue : (A : Obj) → Type₁
  Glue A = Σ[ α ∈ hSet ℓ-zero ] (fst α → Hom 𝟙 A)
  -- The category theory version of this is Σ Obj Glue, equipped with the
  -- functor fst. This is well known as a comma category.

  ⟦_⟧ : (A : Obj) → Glue A
  ⟦ 𝟙 ⟧ = (Unit , isSetUnit) , λ _ → ι
  ⟦ Ans ⟧ = (Bool , isSetBool) , (if_then yes else no)  -- Cool notation.
  ⟦ A ×̇ B ⟧ =
    let α , F = ⟦ A ⟧ in
    let β , G = ⟦ B ⟧ in
      α ×ₛ β , λ (a , b) → ⟨ F a , G b ⟩
  -- The interpretation for function spaces is a pullback.
  -- In set theory (i.e. the computibility predicate approach),
  -- this is formalized as a predicate
  --   C[A⇒B](f) = ∀ (x : term of type A), C[A](x) → C[B](fx)
  -- which defines the computibility predicate on A ⇒ B recursively.
  -- The reader is invited to see why this corresponds to the pullback.
  ⟦ A ⇒ B ⟧ =
    let α , F = ⟦ A ⟧ in
    let β , G = ⟦ B ⟧ in
      (Pullback
        (λ f a → ε * ⟨ f , F a ⟩)
        (G ∘_) ,
      isSetPullback isSetHom (isSet→ (snd β)) (isSet→isGroupoid (isSet→ isSetHom))) ,
      fstₚ


  hom : Hom A B → Glue A → Glue B → Type
  hom f (α , F) (β , G) = Σ[ 𝑓 ∈ (fst α → fst β) ] ∀ a →
    f * F a ≡ G (𝑓 a)  -- Commuting squares

  -- Some more cubical machinery to keep things running smoothly.
  isSethom : ∀ (f : Hom A B) 𝒜 ℬ → isSet (hom f 𝒜 ℬ)
  isSethom _ (α , F) (β , G) = isSetΣ (isSet→ (snd β)) λ _ →
    isSetΠ λ _ → isSet→isGroupoid isSetHom _ _

  isProphom-𝟙 : ∀ {f} → isProp (hom f ⟦ A ⟧ ⟦ 𝟙 ⟧)
  isProphom-𝟙 = isProp× (isProp→ isPropUnit) (isPropΠ λ _ → isSetHom _ _)

  -- We introduce the cases as individual combinators
  -- because we need them later.
  _*̅_ : hom f ⟦ B ⟧ ⟦ C ⟧ → hom g ⟦ A ⟧ ⟦ B ⟧ → hom (f * g) ⟦ A ⟧ ⟦ C ⟧
  (𝑓 , F) *̅ (𝑔 , G) =  -- Functorality
      𝑓 ∘ 𝑔 , λ a → assoc ∙ cong (_ *_) (G a) ∙ F (𝑔 a)

  ι̅ : hom ι ⟦ A ⟧ ⟦ A ⟧
  ι̅ = idfun _ , λ _ → idₗ

  ⟪_,_⟫ : hom f ⟦ A ⟧ ⟦ B ⟧ → hom g ⟦ A ⟧ ⟦ C ⟧ → hom ⟨ f , g ⟩ ⟦ A ⟧ ⟦ B ×̇ C ⟧
  ⟪ (𝑓 , F) , (𝑔 , G) ⟫ =
    (λ a → 𝑓 a , 𝑔 a) ,
    λ a → ⟨⟩-*-distr ∙ cong₂ ⟨_,_⟩ (F a) (G a)

  π̅₁ : hom π₁ ⟦ A ×̇ B ⟧ ⟦ A ⟧
  π̅₁ = fst , λ _ → β₁×

  π̅₂ : hom π₂ ⟦ A ×̇ B ⟧ ⟦ B ⟧
  π̅₂ = snd , λ _ → β₂×

  ε̅ : hom ε ⟦ (A ⇒ B) ×̇ A ⟧ ⟦ B ⟧
  ε̅ = (λ (𝔣 , a) → 𝔣 .sndₚ  a) ,
    λ (𝔣 , a) → funExt⁻ (𝔣 .pathₚ) a

  ƛ̅ : hom f ⟦ A ×̇ B ⟧ ⟦ C ⟧ → hom (ƛ f) ⟦ A ⟧ ⟦ B ⇒ C ⟧
  ƛ̅ {f = f} (𝑓 , F) = 
    (λ a → record {
      fstₚ = ƛ f * snd ⟦ _ ⟧ a ;  -- Term
      sndₚ = 𝑓 ∘ (a ,_) ;  -- Semantics
      pathₚ = funExt λ b → Lemma₂ ∙ F (a , b) } ) ,
    λ _ → refl

  -- There is only one non-trivial coherence that needs to be proved
  -- All the other equations are trivial, apart from
  -- some complicated cubical stuff.
  η̅⇒ : ∀ 𝔣 → PathP (λ i → hom (η⇒ {g = f} i) ⟦ A ⟧ ⟦ B ⇒ C ⟧)
    (ƛ̅ (ε̅ *̅ ⟪ 𝔣 *̅ π̅₁ , π̅₂ ⟫)) 𝔣
  η̅⇒ 𝔣@(𝑓 , F) = ΣPathP (eq-fst ,
    isOfHLevel→isOfHLevelDep 1 {A = _ × _}  -- I need two variables
      {B = λ T → ∀ a → fst T * ⟦ _ ⟧ .snd a ≡ snd T a .fstₚ}
      (λ _ → isPropΠ λ _ → isSetHom _ _)
      (λ _ → refl) F
      (ΣPathP (η⇒ , eq-fst)))
    where
      eq-fst : fst (ƛ̅ (ε̅ *̅ ⟪ 𝔣 *̅ π̅₁ , π̅₂ ⟫)) ≡ 𝑓
      eq-fst = funExt λ a → Pullback≡
        (cong (_* ⟦ _ ⟧ .snd a) η⇒ ∙ F a) refl
        (isSet→Square (isSet→ isSetHom) _ _ _ _)


  -- And we introduce some shorthand to do the cubical nonsense.
  -- Can be safely ignored.
  private
    coh : {f g : Hom A B} (p : f ≡ g)
      → (𝑝 : ⟦ A ⟧ .fst .fst → ⟦ B ⟧ .fst .fst)
      → (F : ∀ a → f * snd ⟦ A ⟧ a ≡ snd ⟦ B ⟧ (𝑝 a))
      → (G : ∀ a → g * snd ⟦ A ⟧ a ≡ snd ⟦ B ⟧ (𝑝 a))
      → PathP (λ i → ∀ a → p i * snd ⟦ A ⟧ a ≡ snd ⟦ B ⟧ (𝑝 a)) F G
    coh p 𝑝 F G i = λ a → isOfHLevel→isOfHLevelDep 1
      {B = λ u → u * snd ⟦ _ ⟧ a ≡ snd ⟦ _ ⟧ (𝑝 a)}
      (λ _ → isSetHom _ _)
      (F a) (G a) p i

  -- We fill in the blanks.
  ⦅_⦆ : (f : Hom A B) → hom f ⟦ A ⟧ ⟦ B ⟧
  ⦅ f * g ⦆ = ⦅ f ⦆ *̅ ⦅ g ⦆
  ⦅ ι ⦆ = ι̅

  ⦅ 𝟙 ⦆ = const _ , λ _ → isPropHom-𝟙 _ _

  ⦅ yes ⦆ = const true , const idᵣ
  ⦅ no ⦆ = const false , const idᵣ

  ⦅ π₁ ⦆ = π̅₁
  ⦅ π₂ ⦆ = π̅₂
  ⦅ ⟨ f , g ⟩ ⦆ = ⟪ ⦅ f ⦆ , ⦅ g ⦆ ⟫

  ⦅ ε ⦆ = ε̅
  ⦅ ƛ f ⦆ = ƛ̅ ⦅ f ⦆

  -- Just (refl, isSetHom), nothing important
  ⦅ idₗ {f = f} i ⦆ = _ , coh idₗ (fst ⦅ f ⦆) (snd (ι̅ *̅ ⦅ f ⦆)) (snd ⦅ f ⦆) i
  ⦅ idᵣ {f = f} i ⦆ = _ , coh idᵣ (fst ⦅ f ⦆) (snd (⦅ f ⦆ *̅ ι̅)) (snd ⦅ f ⦆) i
  ⦅ assoc {f = f} {g = g} {h = h} i ⦆ = _ ,
    coh assoc (fst ⦅ f ⦆ ∘ fst ⦅ g ⦆ ∘ fst ⦅ h ⦆)
      (snd ((⦅ f ⦆ *̅ ⦅ g ⦆) *̅ ⦅ h ⦆))
      (snd (⦅ f ⦆ *̅ (⦅ g ⦆ *̅ ⦅ h ⦆))) i

  ⦅ η₁ tm i ⦆ = isProp→PathP (λ i → isProphom-𝟙 {f = η₁ tm i}) ⦅ 𝟙 ⦆ ⦅ tm ⦆ i

  ⦅ β₁× {f = f} {g = g} i ⦆ = _ ,
    coh β₁× (fst ⦅ f ⦆)
      (snd (π̅₁ *̅ ⟪ ⦅ f ⦆ , ⦅ g ⦆ ⟫))
      (snd ⦅ f ⦆) i
  ⦅ β₂× {f = f} {g = g} i ⦆ = _ ,
    coh β₂× (fst ⦅ g ⦆)
      (snd (π̅₂ *̅ ⟪ ⦅ f ⦆ , ⦅ g ⦆ ⟫))
      (snd ⦅ g ⦆) i
  ⦅ η× {f = f} i ⦆ = _ ,
    coh η× (fst ⦅ f ⦆)
      (snd (⟪ π̅₁ *̅ ⦅ f ⦆ , π̅₂ *̅ ⦅ f ⦆ ⟫))
      (snd ⦅ f ⦆) i

  ⦅ β⇒ {f = f} i ⦆ = _ ,
    coh β⇒ (fst ⦅ f ⦆)
      (snd (ε̅ *̅ ⟪ ƛ̅ ⦅ f ⦆ *̅ π̅₁ , π̅₂ ⟫))
      (snd ⦅ f ⦆) i
  ⦅ η⇒ {g = g} i ⦆ = η̅⇒ ⦅ g ⦆ i

  -- And since we eliminate into a set, the isSetHom constructor is ok.
  ⦅ isSetHom f g x y i j ⦆ = isOfHLevel→isOfHLevelDep 2
    (λ f → isSethom f ⟦ _ ⟧ ⟦ _ ⟧)
    ⦅ f ⦆ ⦅ g ⦆
    (cong ⦅_⦆ x) (cong ⦅_⦆ y)
    (isSetHom f g x y)
    i j

  -- Finally, canonicity.
  canonicity : ∀ ans → (ans ≡ yes) ⊎ (ans ≡ no)
  canonicity ans with ⦅ ans ⦆
  ... | b , p with b _ | p _
  ... | false | p = inr (sym idᵣ ∙ p)
  ... | true  | p = inl (sym idᵣ ∙ p)
  -- The reader is trusted to proceed and prove (Hom 𝟙 Ans ≡ Bool)
-- -}

-- To ease the huge pattern matching like above, I shall define a record.
-- This prevents cubical variables appearing.
module _ {obj : Obj → Type ℓ}
    (⟦_⟧ : (A : Obj) → obj A)
    (hom : ∀ {A B} → obj A → obj B → Hom A B → Type ℓ') where
  record Elim : Type (ℓ-max ℓ ℓ') where
    field
      isSethom : ∀ 𝒜 ℬ (f : Hom A B) → isSet (hom 𝒜 ℬ f)
      _*̅_ : hom ⟦ B ⟧ ⟦ C ⟧ f → hom ⟦ A ⟧ ⟦ B ⟧ g → hom ⟦ A ⟧ ⟦ C ⟧ (f * g)
      ι̅ : hom ⟦ A ⟧ ⟦ A ⟧ ι
      𝟙̅ : hom ⟦ A ⟧ ⟦ 𝟙 ⟧ 𝟙
      idₗ̅ : ∀ 𝔣 → PathP (λ i → hom ⟦ A ⟧ ⟦ B ⟧ (idₗ {f = f} i)) (ι̅ *̅ 𝔣) 𝔣
      idᵣ̅ : ∀ 𝔣 → PathP (λ i → hom ⟦ A ⟧ ⟦ B ⟧ (idᵣ {f = f} i)) (𝔣 *̅ ι̅) 𝔣
      assoc̅ : ∀ 𝔣 𝔤 𝔥 → PathP (λ i → hom ⟦ A ⟧ ⟦ D ⟧ (assoc {f = f} {g = g} {h = h} i))
        ((𝔣 *̅ 𝔤) *̅ 𝔥) (𝔣 *̅ (𝔤 *̅ 𝔥))
      η̅₁ : ∀ f → isProp (hom ⟦ A ⟧ ⟦ 𝟙 ⟧ f)
      y̅ : hom ⟦ 𝟙 ⟧ ⟦ Ans ⟧ yes
      n̅ : hom ⟦ 𝟙 ⟧ ⟦ Ans ⟧ no
      π̅₁ : hom ⟦ A ×̇ B ⟧ ⟦ A ⟧ π₁
      π̅₂ : hom ⟦ A ×̇ B ⟧ ⟦ B ⟧ π₂
      ⟪_,_⟫ : hom ⟦ A ⟧ ⟦ B ⟧ f → hom ⟦ A ⟧ ⟦ C ⟧ g → hom ⟦ A ⟧ ⟦ B ×̇ C ⟧ ⟨ f , g ⟩
      β̅₁× : ∀ 𝔣 𝔤 → PathP (λ i → hom ⟦ A ⟧ ⟦ B ⟧ (β₁× {f = f} {g = g} i))
        (π̅₁ *̅ ⟪ 𝔣 , 𝔤 ⟫) 𝔣
      β̅₂× : ∀ 𝔣 𝔤 → PathP (λ i → hom ⟦ A ⟧ ⟦ B ⟧ (β₂× {f = f} {g = g} i))
        (π̅₂ *̅ ⟪ 𝔣 , 𝔤 ⟫) 𝔤
      η̅× : ∀ 𝔣 → PathP (λ i → hom ⟦ A ⟧ ⟦ B ×̇ C ⟧ (η× {f = f} i))
        (⟪ π̅₁ *̅ 𝔣 , π̅₂ *̅ 𝔣 ⟫) 𝔣
      ε̅ : hom ⟦ (A ⇒ B) ×̇ A ⟧ ⟦ B ⟧ ε
      ƛ̅ : hom ⟦ A ×̇ B ⟧ ⟦ C ⟧ f → hom ⟦ A ⟧ ⟦ B ⇒ C ⟧ (ƛ f)
      β̅⇒ : ∀ 𝔣 → PathP (λ i → hom ⟦ A ×̇ B ⟧ ⟦ C ⟧ (β⇒ {f = f} i))
        (ε̅ *̅ ⟪ ƛ̅ 𝔣 *̅ π̅₁ , π̅₂ ⟫) 𝔣
      η̅⇒ : ∀ 𝔤 → PathP (λ i → hom ⟦ A ⟧ ⟦ B ⇒ C ⟧ (η⇒ {g = g} i))
        (ƛ̅ (ε̅ *̅ ⟪ 𝔤 *̅ π̅₁ , π̅₂ ⟫)) 𝔤

  module Eliminate (elim : Elim) where
    open Elim elim

    ⦅_⦆ : (f : Hom A B) → hom ⟦ A ⟧ ⟦ B ⟧ f
    ⦅_⦆ (isSetHom f g p q i j) =
      isOfHLevel→isOfHLevelDep 2
        (λ f → isSethom ⟦ _ ⟧ ⟦ _ ⟧ f)
        ⦅ f ⦆ ⦅ g ⦆
        (cong ⦅_⦆ p) (cong ⦅_⦆ q)
        (isSetHom f g p q)
        i j
    ⦅ f * g ⦆ = ⦅ f ⦆ *̅ ⦅ g ⦆
    ⦅ ι ⦆ = ι̅
    ⦅ idₗ i ⦆ = idₗ̅ ⦅ _ ⦆ i
    ⦅ idᵣ i ⦆ = idᵣ̅ ⦅ _ ⦆ i
    ⦅ assoc i ⦆ = assoc̅ ⦅ _ ⦆ ⦅ _ ⦆ ⦅ _ ⦆ i
    ⦅ 𝟙 ⦆ = 𝟙̅
    ⦅ η₁ f i ⦆ = isProp→PathP (λ i → η̅₁ (η₁ f i)) ⦅ 𝟙 ⦆ ⦅ f ⦆ i
    ⦅ yes ⦆ = y̅
    ⦅ no ⦆ = n̅
    ⦅ π₁ ⦆ = π̅₁
    ⦅ π₂ ⦆ = π̅₂
    ⦅ ⟨ f , g ⟩ ⦆ = ⟪ ⦅ f ⦆ , ⦅ g ⦆ ⟫
    ⦅ β₁× i ⦆ = β̅₁× ⦅ _ ⦆ ⦅ _ ⦆ i
    ⦅ β₂× i ⦆ = β̅₂× ⦅ _ ⦆ ⦅ _ ⦆ i
    ⦅ η× i ⦆ = η̅× ⦅ _ ⦆ i
    ⦅ ε ⦆ = ε̅
    ⦅ ƛ f ⦆ = ƛ̅ ⦅ f ⦆
    ⦅ β⇒ i ⦆ = β̅⇒ ⦅ _ ⦆ i
    ⦅ η⇒ i ⦆ = η̅⇒ ⦅ _ ⦆ i

normalization.agda

{-# OPTIONS --cubical --no-import-sorts --postfix-projections -W ignore #-}
module normalization where
open import Cubical.Foundations.Prelude
open import Cubical.Foundations.HLevels
open import Cubical.Foundations.Function
open import Cubical.Data.Unit using (Unit; isPropUnit; isSetUnit)
open import Cubical.Data.Bool using (Bool; true; false; if_then_else_; isSetBool)
open import Cubical.Data.Sum using (_⊎_; inr; inl)
open import Cubical.Data.Sigma using (Σ; _×_; ΣPathP)
open import Cubical.Categories.Category
open import Cubical.Categories.Functor
open import Cubical.Categories.NaturalTransformation using (natTrans)
open import Cubical.Categories.Yoneda
open import Cubical.Categories.Presheaf
open import Cubical.Categories.Instances.Sets

module _ where -- Should be in library?
  private variable
    ℓ ℓ' ℓ'' ℓ''' : Level
  Const : (C : Category ℓ ℓ')
    → (D : Category ℓ'' ℓ''')
    → (d : D .Category.ob)
    → Functor C D
  Const C D d .Functor.F-ob c = d
  Const C D d .Functor.F-hom _ = Category.id D
  Const C D d .Functor.F-id = refl
  Const C D d .Functor.F-seq _ _ = sym (Category.⋆IdL D (Category.id D))

open import freeCCC

-- We need to package up some category theory to keep going
-- The Cubical standard library does not have much mechanism
-- for cartesian closed category, but we can do without them.
𝓣 : Category ℓ-zero ℓ-zero
𝓣 .Category.ob = Obj
𝓣 .Category.Hom[_,_] = Hom
𝓣 .Category.id = ι
𝓣 .Category._⋆_ f g = _*_ g f
𝓣 .Category.⋆IdL _ = idᵣ
𝓣 .Category.⋆IdR _ = idₗ
𝓣 .Category.⋆Assoc _ _ _ = sym assoc
𝓣 .Category.isSetHom = isSetHom

-- For normalization, we need to formalize renaming.
-- This is captured in the category as "atomic" contexts.

-- To quote Sterling:
--   For STLC, the correct category of renamings is 
--   "free category with finite products on the set of types".
--   But for dependent type theory, the analogous notion is more complex...
-- It is given by a universal property thus:
--   Let (C, tm[C] -> tp[C]) be the syntactic cwf of your type theory.
--   Then the category of renamings is given by the initial cwf
--   (R, tm[R] -> tp[R]) equipped with a morphism F of cwfs into C such that
--   the induced comparison map tp[R] -> F^* tp[C] is an isomorphism. 
module Atomic where
  infixl 10 _◂_
  data Ctx : Type where
    [] : Ctx
    _◂_ : Ctx → Obj → Ctx
  variable
    Γ Δ Ξ Θ : Ctx

  [_]ᶜ : Ctx → Obj
  [ [] ]ᶜ = 𝟙
  [ Γ ◂ A ]ᶜ = [ Γ ]ᶜ ×̇ A

  infix 9 _∋_  -- Atomic terms (i.e. variables)
  data _∋_ : Ctx → Obj → Type where
    𝕢 : Γ ◂ A ∋ A
    𝕡 : Γ ∋ A → Γ ◂ B ∋ A
  -- TODO Write this and PR into cubical library
  postulate isSet∋ : isSet (Γ ∋ A)
  -- Alternatively we can just add it as a constructor.

  [_]ᵗ : Γ ∋ A → Hom [ Γ ]ᶜ A
  [ 𝕢 ]ᵗ = π₂
  [ 𝕡 v ]ᵗ = [ v ]ᵗ * π₁

  infix 9 _⊇_  -- Atomic substitutions (i.e. renamings)
  data _⊇_ (Γ : Ctx) : Ctx → Type where
    [] : Γ ⊇ []
    _◂_ : Γ ⊇ Δ → Γ ∋ A → Γ ⊇ Δ ◂ A
  postulate isSet⊇ : isSet (Γ ⊇ Δ)

  [_]ˢ : Γ ⊇ Δ → Hom [ Γ ]ᶜ [ Δ ]ᶜ
  [ [] ]ˢ = 𝟙
  [ γ ◂ v ]ˢ = ⟨ [ γ ]ˢ , [ v ]ᵗ ⟩

  infixl 11 _ʷ
  _ʷ : Γ ⊇ Δ → Γ ◂ A ⊇ Δ
  [] ʷ = []
  (γ ◂ v) ʷ = γ ʷ ◂ 𝕡 v

  [_ʷ]ˢ : (γ : Γ ⊇ Δ) → [ γ ʷ ]ˢ ≡ [ γ ]ˢ * π₁ {B = B}
  [ [] ʷ]ˢ = η₁ _
  [ γ ◂ v ʷ]ˢ = cong ⟨_, _ ⟩ [ γ ʷ]ˢ ∙ sym ⟨⟩-*-distr

  𝕚 : ∀ Γ → Γ ⊇ Γ
  𝕚 [] = []
  𝕚 (Γ ◂ A) = 𝕚 Γ ʷ ◂ 𝕢

  𝕚ˢ : ∀ Γ → [ 𝕚 Γ ]ˢ ≡ ι
  𝕚ˢ [] = η₁ _
  𝕚ˢ (Γ ◂ B) = cong ⟨_, π₂ ⟩ ([ 𝕚 Γ ʷ]ˢ ∙ cong (_* π₁) (𝕚ˢ Γ) ∙ idₗ) ∙ ⟨π₁,π₂⟩

  𝕚_ʷ◂𝕢 : ∀ Γ → 𝕚 Γ ʷ ◂ 𝕢 ≡ 𝕚 (Γ ◂ A)
  𝕚 [] ʷ◂𝕢 = refl
  𝕚 Γ ◂ _ ʷ◂𝕢 = refl

  -- Renamings action
  [_]ᵃ : Γ ⊇ Δ → Δ ∋ A → Γ ∋ A
  [ γ ◂ u ]ᵃ 𝕢 = u
  [ γ ◂ u ]ᵃ (𝕡 v) = [ γ ]ᵃ v

  [_ʷ]ᵃ : (γ : Γ ⊇ Δ) (v : Δ ∋ A) → [ γ ʷ ]ᵃ v ≡ 𝕡 {B = B} ([ γ ]ᵃ v)
  [ γ ◂ u ʷ]ᵃ 𝕢 = refl
  [ γ ◂ u ʷ]ᵃ (𝕡 v) = [ γ ʷ]ᵃ v

  𝕚ᵃ : (v : Γ ∋ A) → [ 𝕚 Γ ]ᵃ v ≡ v
  𝕚ᵃ 𝕢 = refl
  𝕚ᵃ (𝕡 v) = [ 𝕚 _ ʷ]ᵃ v ∙ cong 𝕡 (𝕚ᵃ v)

  -- Renaming compositions
  infixl 9 _⊛_
  _⊛_ : Γ ⊇ Δ → Ξ ⊇ Γ → Ξ ⊇ Δ
  [] ⊛ δ = []
  (γ ◂ v) ⊛ δ = (γ ⊛ δ) ◂ [ δ ]ᵃ v

  _ʷ⊛_◂_ : (γ : Γ ⊇ Δ) (δ : Ξ ⊇ Γ) (v : Ξ ∋ A)
    → γ ʷ ⊛ δ ◂ v ≡ γ ⊛ δ
  [] ʷ⊛ δ ◂ v = refl
  (γ ◂ u) ʷ⊛ δ ◂ v = cong (_◂ [ δ ]ᵃ u) (γ ʷ⊛ δ ◂ v)

  ⊛IdL : (γ : Γ ⊇ Δ) → 𝕚 Δ ⊛ γ ≡ γ
  ⊛IdL [] = refl
  ⊛IdL (γ ◂ v) = cong {B = λ _ → _ ⊇ _} (_◂ v)
    ((𝕚 _ ʷ⊛ γ ◂ v) ∙ ⊛IdL γ)  -- TODO correct precedence

  ⊛IdR : (γ : Γ ⊇ Δ) → γ ⊛ 𝕚 Γ ≡ γ
  ⊛IdR [] = refl
  ⊛IdR (γ ◂ v) = cong₂ _◂_ (⊛IdR γ) (𝕚ᵃ v)

  [_]ᵃ[_]ᵃ : (ξ : Θ ⊇ Ξ) (δ : Ξ ⊇ Δ) (v : Δ ∋ A)
    → [ ξ ]ᵃ ([ δ ]ᵃ v) ≡ [ δ ⊛ ξ ]ᵃ v
  [ ξ ]ᵃ[ δ ◂ u ]ᵃ 𝕢 = refl
  [ ξ ]ᵃ[ δ ◂ u ]ᵃ (𝕡 v) = [ ξ ]ᵃ[ δ ]ᵃ v

  ⊛Assoc : (γ : Δ ⊇ Γ) (δ : Ξ ⊇ Δ) (ξ : Θ ⊇ Ξ)
    → (γ ⊛ δ) ⊛ ξ ≡ γ ⊛ (δ ⊛ ξ)
  ⊛Assoc [] δ ξ = refl
  ⊛Assoc (γ ◂ v) δ ξ = cong₂ _◂_ (⊛Assoc γ δ ξ) ([ ξ ]ᵃ[ δ ]ᵃ v)

  [_]ᵗ*[_]ˢ : (v : Δ ∋ A) (δ : Γ ⊇ Δ)
    → [ [ δ ]ᵃ v ]ᵗ ≡ [ v ]ᵗ * [ δ ]ˢ
  [ 𝕢 ]ᵗ*[ δ ◂ u ]ˢ = sym β₂×
  [ 𝕡 v ]ᵗ*[ δ ◂ u ]ˢ
    = [ v ]ᵗ*[ δ ]ˢ
    ∙ cong ([ v ]ᵗ *_) (sym β₁×)
    ∙ sym assoc

  [_]ˢ*[_]ˢ : (γ : Δ ⊇ Ξ) (δ : Γ ⊇ Δ)
    → [ γ ⊛ δ ]ˢ ≡ [ γ ]ˢ * [ δ ]ˢ
  [ [] ]ˢ*[ δ ]ˢ = η₁ _
  [ γ ◂ v ]ˢ*[ δ ]ˢ
    = cong₂ ⟨_,_⟩ [ γ ]ˢ*[ δ ]ˢ [ v ]ᵗ*[ δ ]ˢ
    ∙ sym ⟨⟩-*-distr

  -- Everything we've proved packages into this:
  𝓐 : Category ℓ-zero ℓ-zero
  𝓐 .Category.ob = Ctx
  𝓐 .Category.Hom[_,_] = _⊇_
  𝓐 .Category.id = 𝕚 _
  𝓐 .Category._⋆_ γ δ = δ ⊛ γ
  𝓐 .Category.⋆IdL = ⊛IdR
  𝓐 .Category.⋆IdR = ⊛IdL
  𝓐 .Category.⋆Assoc γ δ ξ = sym (⊛Assoc ξ δ γ)
  𝓐 .Category.isSetHom = isSet⊇

  ρ : Functor 𝓐 𝓣
  ρ .Functor.F-ob = [_]ᶜ
  ρ .Functor.F-hom = [_]ˢ
  ρ .Functor.F-id = 𝕚ˢ _
  ρ .Functor.F-seq γ δ = [ δ ]ˢ*[ γ ]ˢ
open Atomic

-- Next, we define neutral and normal forms.
-- They are presheaves over 𝓐
module Neutral-Normal where
  interleaved mutual
    data Ne : Ctx → Obj {- TODO does this guy need to be functorial? -} → Type
    data Nf : Ctx → Obj → Type

    -- Terminal object
    data Ne where 𝟙 : Ne Γ 𝟙

    -- Product
    data Nf where ⟨_,_⟩ : Nf Γ A → Nf Γ B → Nf Γ (A ×̇ B)
    data Ne where
      π₁ : Ne Γ (A ×̇ B) → Ne Γ A
      π₂ : Ne Γ (A ×̇ B) → Ne Γ B

    -- Exponential
    data Nf where ƛ : Nf (Γ ◂ B) C → Nf Γ (B ⇒ C)
    data Ne where ε : Ne Γ (A ⇒ B) → Nf Γ A → Ne Γ B

    -- Ans
    data Nf where
      yes no : Nf Γ Ans
      ↑ : Ne Γ Ans → Nf Γ Ans

  postulate
    isSetNf : isSet (Nf Γ A)
    isSetNe : isSet (Ne Γ A)

  [_]ⁿᶠ : Γ ⊇ Δ → Nf Δ A → Nf Γ A
  [_]ⁿᵉ : Γ ⊇ Δ → Ne Δ A → Ne Γ A

  [ γ ]ⁿᶠ ⟨ t , s ⟩ = ⟨ [ γ ]ⁿᶠ t , [ γ ]ⁿᶠ s ⟩
  [ γ ]ⁿᶠ (ƛ t) = ƛ ([ γ ʷ ◂ 𝕢 ]ⁿᶠ t)
  [ γ ]ⁿᶠ yes = yes
  [ γ ]ⁿᶠ no = no
  [ γ ]ⁿᶠ (↑ n) = ↑ ([ γ ]ⁿᵉ n)

  [ γ ]ⁿᵉ 𝟙 = 𝟙
  [ γ ]ⁿᵉ (π₁ n) = π₁ ([ γ ]ⁿᵉ n)
  [ γ ]ⁿᵉ (π₂ n) = π₂ ([ γ ]ⁿᵉ n)
  [ γ ]ⁿᵉ (ε f t) = ε ([ γ ]ⁿᵉ f) ([ γ ]ⁿᶠ t)

  [𝕚_]ⁿᶠ : ∀ Γ (t : Nf Γ A) → [ 𝕚 Γ ]ⁿᶠ t ≡ t
  [𝕚_]ⁿᵉ : ∀ Γ (t : Ne Γ A) → [ 𝕚 Γ ]ⁿᵉ t ≡ t

  [𝕚 Γ ]ⁿᶠ ⟨ t , s ⟩ = cong₂ ⟨_,_⟩ ([𝕚 Γ ]ⁿᶠ t) ([𝕚 Γ ]ⁿᶠ s)
  [𝕚 Γ ]ⁿᶠ (ƛ t)
    = cong (λ γ → ƛ ([ γ ]ⁿᶠ t)) 𝕚 Γ ʷ◂𝕢
    ∙ cong ƛ ([𝕚 Γ ◂ _ ]ⁿᶠ t)
  [𝕚 Γ ]ⁿᶠ yes = refl
  [𝕚 Γ ]ⁿᶠ no = refl
  [𝕚 Γ ]ⁿᶠ (↑ n) = cong ↑ ([𝕚 Γ ]ⁿᵉ n)

  [𝕚 Γ ]ⁿᵉ 𝟙 = refl
  [𝕚 Γ ]ⁿᵉ (π₁ n) = cong π₁ ([𝕚 Γ ]ⁿᵉ n)
  [𝕚 Γ ]ⁿᵉ (π₂ n) = cong π₂ ([𝕚 Γ ]ⁿᵉ n)
  [𝕚 Γ ]ⁿᵉ (ε n t) = cong₂ ε ([𝕚 Γ ]ⁿᵉ n) ([𝕚 Γ ]ⁿᶠ t)

  [_]ⁿᶠ[_]ⁿᶠ : (δ : Ξ ⊇ Δ) (γ : Δ ⊇ Γ) (n : Nf Γ A)
    → [ γ ⊛ δ ]ⁿᶠ n ≡ [ δ ]ⁿᶠ ([ γ ]ⁿᶠ n)
  [_]ⁿᵉ[_]ⁿᵉ : (δ : Ξ ⊇ Δ) (γ : Δ ⊇ Γ) (n : Ne Γ A)
    → [ γ ⊛ δ ]ⁿᵉ n ≡ [ δ ]ⁿᵉ ([ γ ]ⁿᵉ n)

  [ δ ]ⁿᶠ[ γ ]ⁿᶠ ⟨ s , t ⟩ = cong₂ ⟨_,_⟩ ([ δ ]ⁿᶠ[ γ ]ⁿᶠ s) ([ δ ]ⁿᶠ[ γ ]ⁿᶠ t)
  [ δ ]ⁿᶠ[ γ ]ⁿᶠ (ƛ n)
    = cong (λ γ → ƛ ([ γ ◂ 𝕢 ]ⁿᶠ n)) (sym (γ ʷ⊛ δ ʷ ◂ 𝕢))
    ∙ cong ƛ ([ δ ʷ ◂ 𝕢 ]ⁿᶠ[ γ ʷ ◂ 𝕢 ]ⁿᶠ n)
  [ δ ]ⁿᶠ[ γ ]ⁿᶠ yes = refl
  [ δ ]ⁿᶠ[ γ ]ⁿᶠ no = refl
  [ δ ]ⁿᶠ[ γ ]ⁿᶠ (↑ n) = cong ↑ ([ δ ]ⁿᵉ[ γ ]ⁿᵉ n)

  [ δ ]ⁿᵉ[ γ ]ⁿᵉ 𝟙 = refl
  [ δ ]ⁿᵉ[ γ ]ⁿᵉ (π₁ n) = cong π₁ ([ δ ]ⁿᵉ[ γ ]ⁿᵉ n)
  [ δ ]ⁿᵉ[ γ ]ⁿᵉ (π₂ n) = cong π₂ ([ δ ]ⁿᵉ[ γ ]ⁿᵉ n)
  [ δ ]ⁿᵉ[ γ ]ⁿᵉ (ε n t) = cong₂ ε ([ δ ]ⁿᵉ[ γ ]ⁿᵉ n) ([ δ ]ⁿᶠ[ γ ]ⁿᶠ t)

  NF : Obj → Functor (𝓐 ^op) (SET ℓ-zero)
  NF A .Functor.F-ob Γ = Nf Γ A , isSetNf
  NF A .Functor.F-hom = [_]ⁿᶠ
  NF A .Functor.F-id = funExt [𝕚 _ ]ⁿᶠ
  NF A .Functor.F-seq γ δ = funExt [ δ ]ⁿᶠ[ γ ]ⁿᶠ

  NE : Obj → Functor (𝓐 ^op) (SET ℓ-zero)
  NE A .Functor.F-ob Γ = Ne Γ A , isSetNe
  NE A .Functor.F-hom = [_]ⁿᵉ
  NE A .Functor.F-id = funExt [𝕚 _ ]ⁿᵉ
  NE A .Functor.F-seq γ δ = funExt [ δ ]ⁿᵉ[ γ ]ⁿᵉ
open Neutral-Normal

module Normalization where
  Psh𝓐 = PreShv 𝓐 ℓ-zero
  Psh𝓣 = PreShv 𝓣 ℓ-zero

  Nerve : Functor 𝓣 Psh𝓐
  -- Nerve A = Hom(ρ(-), A)
  Nerve = funcComp (precomposeF (SET ℓ-zero) (ρ ^opF)) YO

  Glue : Obj → Type₁
  Glue A = Σ[ α̃ ∈ ob ] Hom[ α̃ , F-ob A ]
    where
      open Category Psh𝓐
      open Functor Nerve

  ⟦_⟧ : (A : Obj) → Glue A
  ⟦ 𝟙 ⟧ = Const _ _ (Unit , isSetUnit) ,
    natTrans (λ _ → const 𝟙) λ _ → funExt (const (η₁ _))
  ⟦ Ans ⟧ = NF Ans ,  -- The normal forms
    natTrans (λ _ → nObj) {!   !}
    where
      nObj : Nf Γ Ans → Hom [ Γ ]ᶜ Ans
      nObj yes = yes * 𝟙
      nObj no = no * 𝟙
      nObj (↑ n) = {!   !}
  ⟦ A ×̇ B ⟧ = {!   !} , {!   !}
  ⟦ A ⇒ B ⟧ = {!   !}
{-
  ⟦ 𝟙 ⟧ = (Unit , isSetUnit) , λ _ _ → 𝟙
  ⟦ Ans ⟧ = (Bool , isSetBool) , λ b _ → (if b then yes else no) * 𝟙
  ⟦ A ×̇ B ⟧ =
    let α , F = ⟦ A ⟧ in
    let β , G = ⟦ B ⟧ in
      (α ×ₛ β) , λ (a , b) C → ⟨ F a C , G b C ⟩
  ⟦ A ⇒ B ⟧ =
    let α , F = ⟦ A ⟧ in
    let β , G = ⟦ B ⟧ in
      (Pullback
        (λ f a C → ε * ⟨ f C , F a C ⟩)   -- Term
        (G ∘_) , -- Semantics
      isSetPullback (isSetΠ λ _ → isSetHom) (isSet→ (snd β)) (isSet→isGroupoid (isSet→ (isSetΠ λ _ → isSetHom)))) ,
      fstₚ

  hom : Glue A → Glue B → Hom A B → Type
  hom (α , F) (β , G) f = Σ[ 𝑓 ∈ (fst α → fst β) ] ∀ a C →
    f * F a C ≡ G (𝑓 a) C

  open Elim
  elim : Elim ⟦_⟧ hom
  elim .isSethom _ (β , _) _ = isSetΣ (isSet→ (β .snd)) λ _ →
    isSetΠ λ _ → isSetΠ λ _ → isSet→isGroupoid isSetHom _ _
  elim ._*̅_ (𝑓 , F) (𝑔 , G) = 𝑓 ∘ 𝑔 , λ a C →
    assoc ∙ cong (_ *_) (G a C) ∙ F (𝑔 a) C
  elim .ι̅ = idfun _ , λ _ _ → idₗ

  elim .𝟙̅ = const _ , λ a C → sym (η₁ _)

  elim .y̅ = const true , λ _ _ → refl
  elim .n̅ = const false , λ _ _ → refl

  elim .π̅₁ = fst , λ _ _ → β₁×
  elim .π̅₂ = snd , λ _ _ → β₂×
  elim .⟪_,_⟫ (𝑓 , F) (𝑔 , G) = (λ a → 𝑓 a , 𝑔 a) , λ a C →
    ⟨⟩-*-distr ∙ cong₂ ⟨_,_⟩ (F a C) (G a C)

  elim .ε̅ = (λ (𝔣 , a) → 𝔣 .sndₚ a) , λ (𝔣 , a) C i →
    𝔣 .pathₚ i a C
  elim .ƛ̅ (𝑓 , F) = (λ a → record {
    fstₚ = λ D → {!   !} ;
    sndₚ = {!   !} ;
    pathₚ = {!   !} }) , {!   !}

  elim .idₗ̅ (𝑓 , F) = {!   !}
  elim .idᵣ̅ = {!   !}
  elim .assoc̅ = {!   !}

  elim .η̅₁ = {!   !}

  elim .β̅₁× = {!   !}
  elim .β̅₂× = {!   !}
  elim .η̅× = {!   !}

  elim .β̅⇒ = {!   !}
  elim .η̅⇒ = {!   !}
  -- -}
-- -}

I accidentally discovered something strange. This version (revision 12) of the gist actually used a different glued category than described in @jonsterling 's thesis. Instead of doing the pullback as in the following picture:

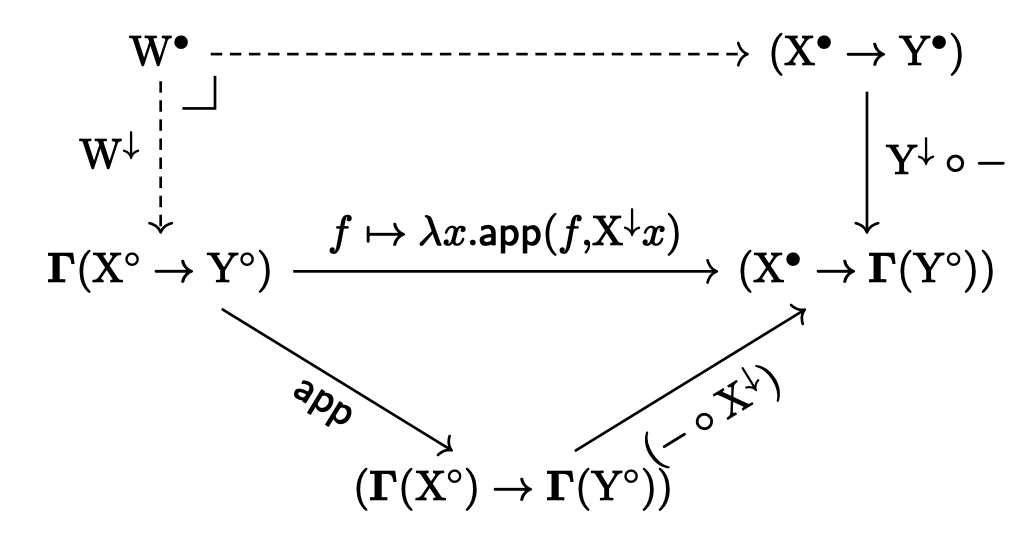
I took a pullback
$$\begin{CD}W^\bullet @>a>> (X^\bullet \to Y^\bullet) \\ @. @. \\ \mathrm{Hom}(X^\circ,Y^\circ) @>>f \mapsto \lambda x. f\circ X^\downarrow x> (X^\bullet \to \mathbf\Gamma(Y^\circ)) \end{CD}$$
(GitHub has janky MathJax, in particular it doesn't seem too happy with @VVV, so no downwards arrow.)

Then the real morphism is given by composing the W → Hom(...) morphism with the currying morphism. This actually all goes through, creating somewhat more proof goals than the usual approach.

@ice1000 Comments? I think this is because the constructed object is actually isomorphic (even if we replace the underlying syntax category with any CCC), and the extra goals serve to prove it.

I think these are equivalent. is the only difference the lower left vertex? if so, you can see that the two choices are isomorphic in SET.

Yes, I see it now. I was overemphasizing it because it initially seemed like I was gluing along an entirely different functor (not Hom(1,-) but inductively defined on types). It just takes formalizing this cat-theoretic-wise for me to realize that. The thing that striked me is that it doesn't use $\epsilon$ at all.

Right! In addition to the fact that what you get out is no longer an object of the glued category, I would say that this hack only works for the global sections functor.

I'll port this to 1lab because there's enough infrastructure there for normalization. This would then become a solver for CCCs.

I just realized I reinvented displayed categories at Line 243 lol