Date: July 8, 2014
In this article, I would like to introduce and explain a data structure I have written in C#. This structure has the ability to store items sorted along "N" dimensions. It is similar in concept to a k-d tree (see Wikipedia), but it is NOT implemented as a binary tree. It branches relative to the number of dimensions its items are being sorted upon.
I developed the structure entirely on my own accord, and since I could not find another implementation like it, I am taking the liberty in giving it a name. I have called the structure an "Omni-Tree".
Background To start, what is a Spacial Partitioning Tree (SPT)? It is a tree that sorts its items on a given number of dimensions. A Quad-Tree is a tree that sorts things on a 2D plane. A Octree is a tree that stores things in 3D space. The reason I have called my tree an "Omni-Tree" is because it can store its items on ANY number of dimensions. Thus, my Omni-Tree can be used to implement Quad-Tree, Oct-Tree, or any other branching dimensional tree.
NOTE: Comprehension of SPT's is required to understand much of this article. If you are unfamiliar with SPT's then I encourage you to research the structures of Quad-Trees and Oct-Trees before if you find yourself lost.
There are two CRUCIAL concepts that people often falsify or overlook when it comes to spacial partitioning data structures:
IMPORTANT CONCEPT #1:
SPT's are NOT limited to floating point coordinates such as in video games. They can be used to sort strings also (as well as nearly any other type). The midpoint of "aaaaaaa" and "ccccccc" could be "bbbbbbb". The string "aaazaaa" would fall between "aaaaaaa" and "bbbbbbb". An example could be sorting people on first names and last names.
The are 2 only requirements of a type to be used for sorting in a SPT is: (1) the type must be comparable, and (2) there must be the ability to get the midpoit (or average) between two variables of that type.
IMPORTANT CONCEPT #2:
Each axis of a spacial partitioning tree does NOT have to be the same type. One axis could be a floating point, and one axis could be strings. For example, you could sort people on first name (string) and date of birth (Datetime) in a single data structure.
COMBINE THOSE CONCEPTS:
When you combine the ability to (1) sort on any number of dimentions, where (2) those dimensions can be nearly any type, and (3) each dimension can be a different type, the Omni-Tree can be used for pretty much anything. You could use an Omni-Tree to represent an SQL Table and keep its items sorted on EVERY column for an example.
Difference from Quad/Oct: Essentially, the data structure is no different than a Quad-Tree or Oct-Tree, but I have made my Omni-Tree COMPLETELY GENERIC (the items or axis do not require an interface), and the number of dimensions has been made dynamic. Also, most of the examples of Quad-Trees and Oct-Trees I have found DO NOT USE FUNCTIONAL PROGRAMMING. Functional programming (using delegates) is fundamental in the process of making generic data structures.
Why Functional Programming: I use functional programming because it allows you to throw ANY object into my data structures WITHOUT inheriting from one or more interfaces. Rather than forcing you to implement functions, you just providing me with those functions when you construct the structure. THIS IS BETTER THAN INTERFACING, because you can have multiple data structures that store the same types, but they may be sorted in different manors based on the delegates passed into my constructors, and you DON'T have to re-write any code (just provide a different delegate).
Generic Declaration: The definition of the tree is public class Omnitree_Linked<T, M>. The T is the type of items that you want to store in the tree, and the M is the types you want those T's to be sorted on. As I said before, each axis in the Omni-Tree can be a different type, and this is accomplished by using an interface on the generic parameter M. An example has been provided in the Using the code section.
What Functions Must Be Provided On Construction: There are 5 parameters on the constructor of my Omni-Tree. There is an example in the "Using the code" section. When I made the Omni-Tree, I tried to break SPT's down to their fundamentals concepts, and I believe I have succeeded in making generic a generic SPT with the minimal amount of necessary input functions (only 3 functions). The parameters on the constructor of an Omni-Tree are: (1) the minimum values of the root node, (2) the maximum values of the root node, (3) a function for how to locate an item along the given dimensions, (4) a function for comparing two values of the axis types, and (5) a function for finding the midpoint (or average) between two variables axis types. NOTE: if you count the generic types, in total my Omni-Tree only requires 7 parameters to construct. Most implementations of SPT's I have seen are extremly complicated, and they require much more than this to construct, and they were not even using generic types.
Shapes: My Omni-Tree is only designed for axis-aligned rectanglular shapes. For 2D trees, this is just a rectangle. For 3D trees, it is a rectangular prism (and so on)… Making a tree that is not axis aligned requires much more computation (slower structure), and the types of the axis must have the ability to do basic algebra (which, if possible, is really hard to do with strings or other non-numeric types). In short, the axis aligned restriction is probably a good thing considering all the negatives that non-axis aligned mathematics brings to the table.
Rules of the Structure (in no particular order): I tried to explain these rules briefly, but understanding them will probably require you to review the source code. (1) All items are stored in the leaves, and NO items are stored in the branches. (2) Each branch in the tree has "log_base2(# sorting dimensions)" children. So for 2D Omni-Trees, each branch has 4 children, and for 3D Omni-Trees, each branch has 8 children. (3) The indexing of the children is an equation of that child is relative to the center of its parent. The equation looks at each axis, and adds "2 ^ D" where "D" is the current dimension of iteration if the child is in the positive direction along that axis. In short, a node that is in an all-positive direction from the center of its parent is computed to have the max index, and a node that is in an all-negative direction from the center of its parent is computed to have an index of 0. (4) The tree grows a branch when adding an item to a leaf would cause that leave to go beyond a specific load amount. This is similar in concept to a load factor in a hash-table. (5) The dimensions of each child in N space is "1 / 2 ^N" the size of its parent, and this resize is equivalent along each of the dimensions. (6) Once established, the dimensions of the nodes in the tree cannot be changed, or the structure would be corrupted. This includes the root. "Index out of bounds" exceptions are possible by adding an item that is outside the bounds of the root of the tree.
Bounds Checking: All the bounds checking is done in the same manor. Rather than checking if a space contains an item, I check to see if a space does not contain an item. This method was not only easy to code, but it is faster when doing space-containing-space operations.
How Does it work (visualzations) Keep in mind that my Omni-Tree can handle multiple dimensions, but in order to explain the structure as a SPT, I will use a 2D Omni-Tree (aka a Quad-Tree).
Lets make a 2D Omni-Tree where the first dimention is of type double, and the second dimension is of type string. The minimum/maximum values we will use are (0.0d, "aaaaaaa") and (10.0d, "zzzzzzz") respectively. Here is the structure:
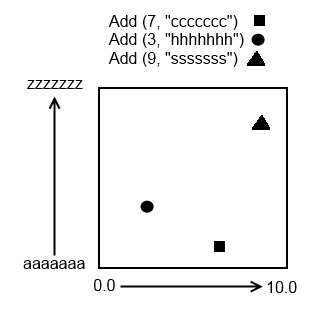
Now lets add some entries:
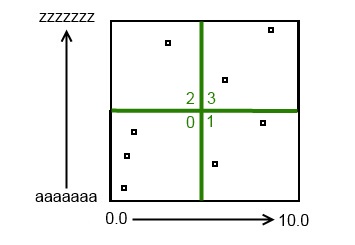
Now lets add multiple items that causes branching. Say we have a current load amount of 7. When we add an 8th item, the tree will divide itself:
So by adding that 8th item. The structure of the Omni-Tree reached its load amount on that leaf (which was the root), and it divided that leaf into 4 four separate leaves, and the root node became a branch. Just for fun, lets add some more items until it grows again:
Hopefully the functionality is fairly clear at this point. However, picture this happening in 3 dimensional space, where a rectangular prism is continually being broken down into smaller nodes. Then think about 4D, 5D, 6D…. I don't even know what to call those shapes, let alone how to visualize them.
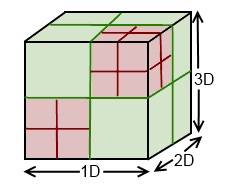
For one final image, here is an examlpe of a 3D Omni-Tree (aka an Oct-Tree):
How do you make an Omni-Tree? The constructor only requires 5 parameters.
// Source Code for Omnitree Constructor:
public Omnitree_Linked(
M[] min, // minimum dimensions for the tree
M[] max, // maximum dimensions for the tree
Locate<T> locate, // a delegate of how to locate an item
Compare<M> compare, // a delegate of how to compare two items
Average<M> average) // a delegate of how to get the midpoint of two items
{
// ...
}Here is an example of calling the above contrustor to build an Octree where each dimension is of type "double", and the Octree has a shape of a rectangular prism with minimum values of (-1000, -1100, -1200) and maximum values of (1200, 1100, 1000) which stores "Model" instances:
using Seven.Structures;
public class Model
{
public double X {get;set;}
public double Y {get;set;}
public double Z {get;set;}
public Model (double x, double y, double z) { X = x; Y = y; Z = z; }
}
// Simple comparison function for doubles
public static Comparison Compare(double left, double right)
{
// NOTE: "Comparison" is jsut an enum
int comparison = left.CompareTo(right);
if (comparison < 0)
return Comparison.Less;
else if (comparison > 0)
return Comparison.Greater;
else
return Comparison.Equal;
}
// IN MAIN------------------------------------------------------------------------
// Example of constructing an Omnitree:
Omnitree<Model, double> omnitree_linked = new Omnitree_Linked<Model, double>(
new double[] { -1000, -1100, -1200 },
new double[] { 1200, 1100, 1000 },
(Model m, out double[] location) => { location = new double[]{ m.X, m.Y, m.Z }; },
Compare, // the function above
(double left, double right) => { return (left + right) * 0.5d; });
// Nows lets add a few Models to the tree
omnitree_linked.Add(new Model(100.0d, -10.743d, 7.0d));
omnitree_linked.Add(new Model(777.77d, -777.7d, 77d));
// Now lets get all the models within a specific area
// The area we are selecting is a rectangular prism
// NOTE: only the first model we added will be within these coordinates
omnitree_linked.Foreach(
(Model m) => { Console.WriteLine(m.X + " " + m.Y + " " + m.Z); },
new double[] { -1000, -1000, -1000 }, // minimum values of the rectangular prism
new double[] { 500, 500, 500 }); // maximum values of the rectangular prismWait! I said that each dimension could be a different type, but the above example only uses doubles. Well, all you have to do is make an interface. It may not be the prettiest thing you've ever seen, but it works… And it was the only way I have come up with so far to do it generically for any number of dimensions. Here is an example of an Omni-Tree sorted by different types along each dimension:
NOTE: in this example I just used "object" as the interface, but you could easily make your own.
using Seven.Structures;
public class Person
{
public double Money {get;set;}
public string Name {get;set;}
public Person(double m, string n) { Money = m; Name = n; }
}
public static Comparison Compare(object left, object right)
{
if (left is string && right is string)
{
int comparison = ((string)left).CompareTo((string)right);
if (comparison < 0)
return Comparison.Less;
else if (comparison > 0)
return Comparison.Greater;
else
return Comparison.Equal;
}
if (left is double && right is double)
{
int comparison = ((double)left).CompareTo((double)right);
if (comparison < 0)
return Comparison.Less;
else if (comparison > 0)
return Comparison.Greater;
else
return Comparison.Equal;
}
throw new System.Exception("invalid omni-tree dimension values");
}
public static object MidPoint(object left, object right)
{
if (left is string && right is string)
{
// This average function requires the strings be the same length
// you can make a better string-averager than this simple example...
char[] mid = new char[((string)left).Length];
for (int i = 0; i < ((string)left).Length; i++)
mid[i] = (char)((((string)left)[i] + ((string)right)[i]) / 2);
}
if (left is double && right is double)
{
return ((double)left + (double)right) * 0.5d;
}
throw new System.Exception("invalid omni-tree dimension values");
}
// IN MAIN----------------------------------------------------------------------
// Example of constructing an Omnitree:
Omnitree<Person, object> omnitree_linked = new Omnitree_Linked<Person, object>(
new object[] { -1000.0d, "aaaaaaa" },
new object[] { 1000.0d, "zzzzzzz" },
(Person p, out object[] location) => { location = new object[]{ p.Money, p.Name }; },
Compare, // the function above
MidPoint); // the function above
// Nows lets add a few Models to the tree
omnitree_linked.Add(new Person(100.00d, "bobby"));
omnitree_linked.Add(new Person(77.7d, "seven"));
// And the traversal...
omnitree_linked.Foreach(
(Person p) => { Console.WriteLine(p.Name + " " + p.Money); },
new object[] { 0.00d, "aaaaa" }, // minumum dimensions
new object[] { 80.0d, "ttttt" }); // maximum dimensionsNOTE: the tree provided in the source code is not fully optimized by any means, but the pros/cons below should remain constant no matter how optimized the structure is.
Here are some reasons TO use an Omni-Tree:
- It is short, clean, and easy to implement as opposed to many other methods of multi-dimensional sorting. People reading it will clearly understand that you are keeping those items sorted on every dimension.
- It provides FAST look ups. This is the largest benefit to using the structure. Because it keeps its items sorted, it will have very fast look up times as long as the data is pretty evenly distributed along the dimensions of the tree.
- Additions/subtractions after initial population should never cause an entire re-construction of the structure (as with the "re-hash" of a hash table or the "re-allocation" of list-arrays). If it does cause an entire reconstruction, it is because you added the same item to the tree a bunch of times, adn then you removed all of them at once.
- When you need to get nearest neighbors of node. This is an EXTREME optimization for collision detection in real-time physics engines.
- The structure of a SPT can be used to efficiently track statistical data such as for clustering algorithms in mass artificial intelligence systems.
There are surely more benefits that I simply an not considering at this time…
Here are some reasons NOT TO use an Omni-Tree:
- The Omni-Tree may require large amounts of memory (especially on a large # of sorting dimensions), but this varies wildely basedon the data.
- The worst case occurs when all the items being added to are very close to each other and not very evenly distributed, because it will result in a lot of branching in that specific area of the tree. So if you know data is dense in specific areas, make the Omni-Tree the proper size for that area, or avoid the use of an Omni-Tree (or possibly customize the tree to have a node bias).
- If you constantly need to call a "foreach" on every item in the tree, you probably don't want to use an Omni-Tree.
- The initial construction/population time can be quite costly.
If you only want an Oct/Quad tree, all you have to do is remove the dynamic nature of the dimensions. The Seven framework (see link at top of file) should include implementations for both Oct and Quad trees.
I encourage you to use Quad/Oct-Trees when you are storing items in traditional floating point dimensions, because anyone reading your code should have a very clear idea of what is going on. This is just a naming convention.
IEnumerable is Outdated
The "IEnumerable" class in the .NET framework was a nice attempt at generic iteration, but IT IS NOT AS GOOD AS DELEGATE TRAVERSALS. Using delegate traversals of data structures is (1) faster, (2) never requires extra memory (even for recursive data structures), (3) you can change items in the structure AS YOU ITERATE using ref parameters on the delegate, and (4) MOST IMPORTANTLY delegate traversals can have custom traversals of the structure. In short, stop using "foreach" loops pretty much alltogether, and start using delegates. Besides their syntax can be made to be very similar:
// IEnumerable
foreach (int i in list) { do something }
// Delegate (THIS IS BETTER!) ... except on arrays, see below
list.Foreach((int i) => { do something });You can do everything with a delegate traversal that you can with a IEnumerable "foreach" traversal. You can even break/restart the iteration by returning a value in the delegate.
NOTE: for anyone that tries to speed test foreach loops on arrays in C#, know that the compiler will optimize those loops (unroll them). In short, cast the array as an "IEnumerable", store it in a temporary variable, and then try to foreach that IEnumerable variable.
Author Edit (2020.7.26): I have striken out this section of the article because I no longer agree with the opnions I expressed. As of this comment I still prefer alternatives to the IEnumerable pattern, but there is an even better alternative to using delegates.
In this section I will show an example of a speed test of using Omni-Trees vs a standard System.Collections.Generic.List from the .NET Framework. This is NOT an end-all test. It is simply a test I scrapped together that illistrates the basic pros/cons of the structures.
Here is the source code:
public static void Test_LIST()
{
Stopwatch timer = new Stopwatch();
int iterations = 10000000;
Console.WriteLine("LIST------------------------");
System.Collections.Generic.List<Tuple<double, double, double>> list =
new System.Collections.Generic.List<Tuple<double, double, double>>();
timer.Restart();
for (int i = -iterations; i < iterations; i++)
list.Add(new Tuple<double, double, double>(i, i, i));
timer.Stop();
Console.WriteLine("ADD TIME: " + timer.ElapsedMilliseconds / 1000.0d);
timer.Restart();
int count = 0;
foreach (Tuple<double, double, double> i in list)
{
if (
i.Item1 >= 0 && i.Item1 <= 25000000 &&
i.Item2 >= 0 && i.Item2 <= 25000000 &&
i.Item3 >= 0 && i.Item3 <= 25000000)
count++;
}
timer.Stop();
Console.WriteLine("FOREACH (25000000):");
Console.WriteLine(" Items Found: " + count);
Console.WriteLine(" Time Elapsed (sec): " + timer.ElapsedMilliseconds / 1000.0d);
timer.Restart();
count = 0;
foreach (Tuple<double, double, double> i in list)
{
if (
i.Item1 >= 0 && i.Item1 <= 250000 &&
i.Item2 >= 0 && i.Item2 <= 250000 &&
i.Item3 >= 0 && i.Item3 <= 250000)
count++;
}
timer.Stop();
Console.WriteLine("FOREACH (250000):");
Console.WriteLine(" Items Found: " + count);
Console.WriteLine(" Time Elapsed (sec): " + timer.ElapsedMilliseconds / 1000.0d);
timer.Restart();
count = 0;
foreach (Tuple<double, double, double> i in list)
{
if (
i.Item1 >= 0 && i.Item1 <= 2500 &&
i.Item2 >= 0 && i.Item2 <= 2500 &&
i.Item3 >= 0 && i.Item3 <= 2500)
count++;
}
timer.Stop();
Console.WriteLine("FOREACH (2500):");
Console.WriteLine(" Items Found: " + count);
Console.WriteLine(" Time Elapsed (sec): " + timer.ElapsedMilliseconds / 1000.0d);
timer.Restart();
count = 0;
foreach (Tuple<double, double, double> i in list)
{
if (
i.Item1 >= 0 && i.Item1 <= 25 &&
i.Item2 >= 0 && i.Item2 <= 25 &&
i.Item3 >= 0 && i.Item3 <= 25)
count++;
}
timer.Stop();
Console.WriteLine("FOREACH (25):");
Console.WriteLine(" Items Found: " + count);
Console.WriteLine(" Time Elapsed (sec): " + timer.ElapsedMilliseconds / 1000.0d);
}public static void Test_OMNITREE()
{
Stopwatch timer = new Stopwatch();
int iterations = 10000000;
Console.WriteLine("OMNITREE-------------------");
Omnitree<int, double> omnitree_linked = new Omnitree_Linked<int, double>(
new double[] { -iterations - 1, -iterations - 1, -iterations - 1 },
new double[] { iterations + 1, iterations + 1, iterations + 1 },
(int i, out double[] location) => { location = new double[] { i, i, i }; },
Program.Compare, // just a comparison function...
(double left, double right) => { return (left + right) * 0.5d; },
10000);
timer.Restart();
for (int i = -iterations; i < iterations; i++)
omnitree_linked.Add(i);
timer.Stop();
Console.WriteLine("ADD TIME: " + timer.ElapsedMilliseconds / 1000.0d);
timer.Restart();
int count2 = 0;
omnitree_linked.Foreach(
(int current) => { count2++; },
new double[] { 0, 0, 0 },
new double[] { 25000000, 25000000, 25000000 });
timer.Stop();
Console.WriteLine("FOREACH (250000):");
Console.WriteLine(" Items Found: " + count2);
Console.WriteLine(" Time Elapsed (sec): " + timer.ElapsedMilliseconds / 1000.0d);
timer.Restart();
count2 = 0;
omnitree_linked.Foreach(
(int current) => { count2++; },
new double[] { 0, 0, 0 },
new double[] { 250000, 250000, 250000 });
timer.Stop();
Console.WriteLine("FOREACH (250000):");
Console.WriteLine(" Items Found: " + count2);
Console.WriteLine(" Time Elapsed (sec): " + timer.ElapsedMilliseconds / 1000.0d);
timer.Restart();
count2 = 0;
omnitree_linked.Foreach(
(int current) => { count2++; },
new double[] { 0, 0, 0 },
new double[] { 2500, 2500, 2500 });
timer.Stop();
Console.WriteLine("FOREACH (2500):");
Console.WriteLine(" Items Found: " + count2);
Console.WriteLine(" Time Elapsed (sec): " + timer.ElapsedMilliseconds / 1000.0d);
timer.Restart();
count2 = 0;
omnitree_linked.Foreach(
(int current) => { count2++; },
new double[] { 0, 0, 0 },
new double[] { 25, 25, 25 });
timer.Stop();
Console.WriteLine("FOREACH (25):");
Console.WriteLine(" Items Found: " + count2);
Console.WriteLine(" Time Elapsed (sec): " + timer.ElapsedMilliseconds / 1000.0d);
}Here is the output I got on my machine:
LIST------------------------
ADD TIME: 2.186
FOREACH (25000000):
Items Found: 10000000
Time Elapsed (sec): 0.101
FOREACH (250000):
Items Found: 250001
Time Elapsed (sec): 0.096
FOREACH (2500):
Items Found: 2501
Time Elapsed (sec): 0.091
FOREACH (25):
Items Found: 26
Time Elapsed (sec): 0.092
OMNITREE-------------------
ADD TIME: 22.573
FOREACH (25000000):
Items Found: 10000000
Time Elapsed (sec): 0.471
FOREACH (250000):
Items Found: 250001
Time Elapsed (sec): 0.012
FOREACH (2500):
Items Found: 2501
Time Elapsed (sec): 0
FOREACH (25):
Items Found: 26
Time Elapsed (sec): 0
- As you can see, the initial population took considerable more time than a simple list (which is expected). Keep in mind we are dealing with 10,000,000 items here. And there is definitely more optimization that can be done on the structure as of writing this test case, but it will never be as fast as adding to a list.
- Once constructed the Omni-Tree had much faster look-up times than the List. I included the first test case as an example. DON'T QUERY NEARLY THE ENTIRE STRUCTURE. Instead, just use the "Foreach" method overload that takes no min/max parameters. This will iterate through all the items without doing a bunch of floating point comparisons. Again, iterating through the entire structure will never be as fast as with a list.
KEEP IN MIND!!! This test is ONLY testing initial population and look-ups. The structure of the Omni-Tree can be used for other purposes too (see "Why use my Omni-Tree").
If anyone would be willing to provide me with a k-d-tree in C# I will gladly test that implementation against mine (once i get mine a bit more optimized). But I have yet to run across a decent open source k-d-tree, so I cannot test it.
If used correctly and in the appropriate situations, using my Omni-Tree has the potential to greatly optimize your code, as well as simplify code using other techniques of dimensional sorting. It is easy to use, but mastering when/how to use the structure takes a lot of knowlege about how the structure works.
I am excited to write this article because I have re-written the data structure about 5 times now and I believe I have nearly perfected my general design. I have never seen an SPT as easy to create/manipulate as the one I have developed (at least in the open source community). I hope you find the structure as easy to use as I beleive I've made it. Feedback is appreciated. 🙂
Thanks.
I tried to explain my Omni-Tree in a brief manor with enough information to get the concept across. However, if this article was too complicated/poorly-written this may help you out: Go to the source code of the Omni-Tree, and look for the methods "GrowBranch", and "GrowLeaf". These two functions are called when the structure must divide itself. Examining the changes made in those two functions is crucial to understand how the entire structure works. Print out the dimensions of the new nodes if you need to see them. Hope that helps.