|
""" |
|
The main PythTB module consists of these two classes: |
|
|
|
* :class:`pythtb.tb_model` main class describing tight-binding model, |
|
|
|
* :class:`pythtb.wf_array` class used to compute some properties of |
|
electron wavefunctions on a regular grid, like Berry phase and Berry |
|
curvature, |
|
|
|
and an additional function: |
|
|
|
* :func:`pythtb.k_path`. |
|
|
|
""" |
|
|
|
# PythTB python tight binding module. |
|
# Version 1.6.1, Nov 6, 2012 |
|
|
|
# Copyright 2010, 2012 by Sinisa Coh and David Vanderbilt |
|
# |
|
# This file is part of PythTB. PythTB is free software: you can |
|
# redistribute it and/or modify it under the terms of the GNU General |
|
# Public License as published by the Free Software Foundation, either |
|
# version 3 of the License, or (at your option) any later version. |
|
# |
|
# PythTB is distributed in the hope that it will be useful, but WITHOUT |
|
# ANY WARRANTY; without even the implied warranty of MERCHANTABILITY |
|
# or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public |
|
# License for more details. |
|
# |
|
# A copy of the GNU General Public License should be available |
|
# alongside this source in a file named gpl-3.0.txt. If not, |
|
# see <http://www.gnu.org/licenses/>. |
|
# |
|
# PythTB is availabe at http://www.physics.rutgers.edu/pythtb/ |
|
|
|
import numpy as np # numerics for matrices |
|
import sys # for exiting |
|
import copy # for deepcopying |
|
try: |
|
import matplotlib.pyplot as pl |
|
except: |
|
print "Unable to load pyplot! Function tb_model.visualize(...) will not work!" |
|
|
|
class tb_model: |
|
r""" |
|
This is the main class of the PythTB package which contains all |
|
information for the tight-binding model. |
|
|
|
:param dim_k: Dimensionality of reciprocal space, i.e., specifies how |
|
many directions are considered to be periodic. |
|
|
|
:param dim_r: Dimensionality of real space, i.e., specifies how many |
|
real space lattice vectors there are and how many coordinates are |
|
needed to specify the orbital coordinates. |
|
|
|
.. note:: Parameter *dim_r* can be larger than *dim_k*! For example, |
|
a polymer is a three-dimensional molecule (one needs three |
|
coordinates to specify orbital positions), but it is periodic |
|
along only one direction. For a polymer, therefore, we should |
|
have *dim_k* equal to 1 and *dim_r* equal to 3. See similar example |
|
here: :ref:`trestle-example`. |
|
|
|
:param lat: Array containing lattice vectors in Cartesian |
|
coordinates (in arbitrary units). In example the below, the first |
|
lattice vector has coordinates [1.0,0.5] while the second |
|
one has coordinates [0.0,2.0]. |
|
|
|
:param orb: Array containing reduced coordinates of all |
|
tight-binding orbitals. In the example below, the first |
|
orbital is defined with reduced coordinates [0.2,0.3]. Its |
|
Cartesian coordinates are therefore 0.2 times the first |
|
lattice vector plus 0.3 times the second lattice vector. |
|
|
|
:param per: This is an optional parameter giving a list of lattice |
|
vectors which are considered to be periodic. In the example below, |
|
only the vector [0.0,2.0] is considered to be periodic (since |
|
per=[1]). By default, all lattice vectors are assumed to be |
|
periodic. If dim_k is smaller than dim_r, then by default the first |
|
dim_k vectors are considered to be periodic. |
|
|
|
Example usage:: |
|
|
|
# Creates model that is two-dimensional in real space but only |
|
# one-dimensional in reciprocal space. Second lattice vector is |
|
# chosen to be periodic (since per=[1]). Three orbital |
|
# coordinates are specified. |
|
tb = tb_model(1, 2, |
|
lat=[[1.0, 0.5], [0.0, 2.0]], |
|
orb=[[0.2, 0.3], [0.1, 0.1], [0.2, 0.2]], |
|
per=[1]) |
|
|
|
""" |
|
|
|
def __init__(self,dim_k,dim_r,lat,orb,per=None): |
|
|
|
# initialize _dim_k = dimensionality of k-space (integer) |
|
if type(dim_k).__name__!='int': |
|
raise Exception("Argument dim_k not an integer") |
|
if dim_k < 0 or dim_k > 4: |
|
raise Exception("Argument dim_k out of range. Must be between 0 and 4.") |
|
self._dim_k=dim_k |
|
|
|
# initialize _dim_r = dimensionality of r-space (integer) |
|
if type(dim_r).__name__!='int': |
|
raise Exception("Argument dim_r not an integer") |
|
if dim_r < dim_k or dim_r > 4: |
|
raise Exception("Argument dim_r out of range. Must be dim_r>=dim_k and dim_r<=4.") |
|
self._dim_r=dim_r |
|
|
|
# initialize _lat = lattice vectors, array of dim_r*dim_r |
|
# format is _lat(lat_vec_index,cartesian_index) |
|
# special option: 'unit' implies unit matrix |
|
if lat=='unit': |
|
self._lat=np.identity(dim_r,float) |
|
elif type(lat).__name__ not in ['list','ndarray']: |
|
raise Exception("Argument lat is not a list.") |
|
else: |
|
self._lat=np.array(lat,dtype=float) |
|
if self._lat.shape!=(dim_r,dim_r): |
|
raise Exception("Wrong lat array dimensions") |
|
|
|
# initialize _norb = number of basis orbitals per cell |
|
# and _orb = orbital locations, in reduced coordinates |
|
# format is _orb(orb_index,lat_vec_index) |
|
# special option: 'bravais' implies one atom at origin |
|
if (orb=='bravais'): |
|
self._norb=1 |
|
self._orb=np.zeros((1,dim_r)) |
|
elif type(orb).__name__ not in ['list','ndarray']: |
|
raise Exception("Argument orb is not a list") |
|
else: |
|
self._orb=np.array(orb,dtype=float) |
|
if len(self._orb.shape)!=2: |
|
raise Exception("Wrong orb array rank") |
|
self._norb=self._orb.shape[0] # number of orbitals |
|
if self._orb.shape[1]!=dim_r: |
|
raise Exception("Wrong orb array dimensions") |
|
|
|
# choose which self._dim_k out of self._dim_r dimensions are |
|
# to be considered periodic. |
|
if per==None: |
|
# by default first _dim_k dimensions are periodic |
|
self._per=range(self._dim_k) |
|
else: |
|
if len(per)!=self._dim_k: |
|
raise Exception("Wrong choice of periodic/infinite direction!") |
|
# store which directions are the periodic ones |
|
self._per=per |
|
|
|
# Initialize onsite energies to zero |
|
self._site_energies=np.zeros(self._norb,dtype=float) |
|
# remember which onsite energies user has specified |
|
self._site_energies_specified=np.zeros(self._norb,dtype=bool) |
|
self._site_energies_specified[:]=False |
|
|
|
# Initialize hoppings to empty list |
|
self._hoppings=[] |
|
|
|
# The onsite energies and hoppings are not specified |
|
# when creating a 'tb_model' object. They are speficied |
|
# subsequently by separate function calls defined below. |
|
|
|
def set_onsite(self,onsite_en,ind_i=None,mode="set"): |
|
r""" |
|
Defines on-site energies for tight-binding orbitals. One can |
|
either set energy for one tight-binding orbital, or all at |
|
once. |
|
|
|
.. warning:: In previous version of PythTB this function was |
|
called *set_sites*. For backwards compatibility one can still |
|
use that name but that feature will be removed in future |
|
releases. |
|
|
|
:param onsite_en: Either a list of real numbers specifying for |
|
each orbital its on-site energy (in arbitrary units), or a |
|
single on-site energy (in this case *ind_i* parameter must |
|
be given). If this function is never called, on-site energy |
|
is assumed to be zero. |
|
|
|
:param ind_i: Index of tight-binding orbital whose on-site |
|
energy you wish to change. This parameter should be |
|
specified only when *onsite_en* is a single number (not a |
|
list). |
|
|
|
:param mode: Similar to parameter *mode* in function |
|
*set_hop*. Speficies way in which parameter *onsite_en* is |
|
used. It can either set value of on-site energy from scratch, |
|
reset it, or add to it. |
|
|
|
* "set" -- Default value. On-site energy is set to value of |
|
*onsite_en* parameter. One can use "set" on each |
|
tight-binding orbital only once. |
|
|
|
* "reset" -- Specifies on-site energy to given value. This |
|
function can be called multiple times for the same |
|
orbital(s). |
|
|
|
* "add" -- Adds to the previous value of on-site |
|
energy. This function can be called multiple times for the |
|
same orbital(s). |
|
|
|
Example usage:: |
|
|
|
# Defines on-site energy of first orbital to be 0.0, |
|
# second 1.0, and third 2.0 |
|
tb.set_onsite([0.0, 1.0, 2.0]) |
|
# Increases value of on-site energy for second orbital |
|
tb.set_onsite(100.0, 1, mode="add") |
|
# Changes on-site energy of second orbital to zero |
|
tb.set_onsite(0.0, 1, mode="reset") |
|
# Sets all three on-site energies at once |
|
tb.set_onsite([2.0, 3.0, 4.0], mode="reset") |
|
|
|
""" |
|
if ind_i==None: |
|
if (len(onsite_en)!=self._norb): |
|
raise Exception("Wrong number of site energies") |
|
# make sure that onsite terms are not complex |
|
if np.max(np.abs(np.imag(onsite_en)))>1.0E-8: |
|
raise Exception("Onsite energy should not have imaginary part!") |
|
# specifying onsite energies from scratch, can be called only once |
|
if mode.lower()=="set": |
|
# specifying only one site at a time |
|
if ind_i!=None: |
|
# make sure we specify things only once |
|
if self._site_energies_specified[ind_i]==True: |
|
raise Exception("Onsite energy for this site was already specified! Use mode=\"reset\" or mode=\"add\".") |
|
else: |
|
self._site_energies[ind_i]=onsite_en |
|
self._site_energies_specified[ind_i]=True |
|
# specifying all sites at once |
|
else: |
|
# make sure we specify things only once |
|
if True in self._site_energies_specified[ind_i]: |
|
raise Exception("Some or all onsite energies were already specified! Use mode=\"reset\" or mode=\"add\".") |
|
else: |
|
self._site_energies[:]=onsite_en |
|
self._site_energies_specified[:]=True |
|
# reset values of onsite terms, without adding to previous value |
|
elif mode.lower()=="reset": |
|
# specifying only one site at a time |
|
if ind_i!=None: |
|
self._site_energies[ind_i]=onsite_en |
|
self._site_energies_specified[ind_i]=True |
|
# specifying all sites at once |
|
else: |
|
self._site_energies[:]=onsite_en |
|
self._site_energies_specified[:]=True |
|
# add to previous value |
|
elif mode.lower()=="add": |
|
# specifying only one site at a time |
|
if ind_i!=None: |
|
self._site_energies[ind_i]+=onsite_en |
|
self._site_energies_specified[ind_i]=True |
|
# specifying all sites at once |
|
else: |
|
self._site_energies[:]+=onsite_en |
|
self._site_energies_specified[:]=True |
|
else: |
|
raise Exception("Wrong value of mode parameter") |
|
|
|
def set_hop(self,hop_amp,ind_i,ind_j,ind_R=None,mode="set",allow_conjugate_pair=False): |
|
r""" |
|
|
|
Defines hopping parameters between tight-binding orbitals. In |
|
the notation used in section 3.1 equation 3.6 of |
|
:download:`notes on tight-binding formalism |
|
<misc/pythtb-formalism.pdf>` this function specifies the |
|
following object |
|
|
|
.. math:: |
|
|
|
H_{ij}({\bf R})= \langle \phi_{{\bf 0} i} \vert H \vert \phi_{{\bf R},j} \rangle |
|
|
|
Where :math:`\langle \phi_{{\bf 0} i} \vert` is i-th |
|
tight-binding orbital in the home unit cell and |
|
:math:`\vert \phi_{{\bf R},j} \rangle` is j-th tight-binding orbital in |
|
unit cell shifted by lattice vector :math:`{\bf R}`. :math:`H` |
|
is the Hamiltonian. |
|
|
|
(Strictly speaking, this term specifies hopping amplitude |
|
for hopping from site *j+R* to site *i*, not vice-versa.) |
|
|
|
Hopping in the opposite direction is automatically included by |
|
the code since |
|
|
|
.. math:: |
|
|
|
H_{ji}(-{\bf R})= \left[ H_{ij}({\bf R}) \right]^{*} |
|
|
|
.. warning:: |
|
|
|
Do not specify hopping in both |
|
:math:`i \rightarrow j+R` direction and opposite |
|
:math:`j \rightarrow i-R` direction! Nevertheless, if you |
|
really want to do this and you know what you are doing, see |
|
description of parameter *allow_conjugate_pair*. |
|
|
|
.. warning:: In previous version of PythTB this function was |
|
called *add_hop*. For backwards compatibility one can still |
|
use that name but that feature will be removed in future |
|
releases. |
|
|
|
:param hop_amp: Hopping amplitude; can be real or complex number, |
|
equals :math:`H_{ij}({\bf R})`. |
|
|
|
:param ind_i: Index of bra orbital from the bracket :math:`\langle |
|
\phi_{{\bf 0} i} \vert H \vert \phi_{{\bf R},j} \rangle`. This |
|
orbital is assumed to be in the home unit cell. |
|
|
|
:param ind_j: Index of ket orbital from the bracket :math:`\langle |
|
\phi_{{\bf 0} i} \vert H \vert \phi_{{\bf R},j} \rangle`. This |
|
orbital does not have to be in the home unit cell; its unit cell |
|
position is determined by parameter *ind_R*. |
|
|
|
:param ind_R: Specifies, in reduced coordinates, the shift of |
|
the ket orbital. The number of coordinates must equal the |
|
dimensionality in real space (*dim_r* parameter) for consistency, |
|
but only the periodic directions of ind_R will be considered. If |
|
reciprocal space is zero-dimensional (as in a molecule), |
|
this parameter does not need to be specified. |
|
|
|
:param mode: Similar to parameter *mode* in function |
|
*set_onsite*. Speficies way in which parameter *hop_amp* is |
|
used. It can either set value of hopping term from scratch, |
|
reset it, or add to it. |
|
|
|
* "set" -- Default value. Hopping term is set to value of |
|
*hop_amp* parameter. One can use "set" for each triplet of |
|
*ind_i*, *ind_j*, *ind_R* only once. |
|
|
|
* "reset" -- Specifies on-site energy to given value. This |
|
function can be called multiple times for the same triplet |
|
*ind_i*, *ind_j*, *ind_R*. |
|
|
|
* "add" -- Adds to the previous value of hopping term This |
|
function can be called multiple times for the same triplet |
|
*ind_i*, *ind_j*, *ind_R*. |
|
|
|
If *allow_conjugate_pair* was ever set to True, then it is |
|
possible that user has specified both :math:`i \rightarrow j+R` |
|
and conjugate pair :math:`j \rightarrow i-R`. |
|
In this case, "set", "reset", and "add" |
|
parameters will treat triplet *ind_i*, *ind_j*, *ind_R* and |
|
conjugate triplet *ind_j*, *ind_i*, *-ind_R* as distinct. |
|
|
|
:param allow_conjugate_pair: Default value is *False*. If set |
|
to *True* code will allow user to specify hopping |
|
:math:`i \rightarrow j+R` even if conjugate-pair hopping |
|
:math:`j \rightarrow i-R` has been |
|
specified. Beware, if both terms are specified, code will |
|
still count each term two times. This parameter should be |
|
used very rarely by regular user. Please understand well |
|
what code is doing before setting this parameter to True. |
|
|
|
Example usage:: |
|
|
|
# Specifies complex hopping amplitude between first orbital in home |
|
# unit cell and third orbital in neigbouring unit cell. |
|
tb.set_hop(0.3+0.4j, 0, 2, [0, 1]) |
|
# change value of this hopping |
|
tb.set_hop(0.1+0.2j, 0, 2, [0, 1], mode="reset") |
|
# add to previous value (after this function call below, |
|
# hopping term amplitude is 100.1+0.2j) |
|
tb.set_hop(100.0, 0, 2, [0, 1], mode="add") |
|
|
|
""" |
|
# |
|
if self._dim_k!=0 and ind_R==None: |
|
raise Exception("Need to specify ind_R!") |
|
# if necessary convert from integer to array |
|
if self._dim_k==1 and type(ind_R).__name__=='int': |
|
tmpR=np.zeros(self._dim_r,dtype=int) |
|
tmpR[self._per]=ind_R |
|
ind_R=tmpR |
|
# check length of ind_R |
|
if self._dim_k!=0: |
|
if len(ind_R)!=self._dim_r: |
|
raise Exception("Length of input ind_R vector must equal dim_r! Even if dim_k<dim_r.") |
|
# |
|
# do not allow onsite hoppings to be specified here because then they |
|
# will be double-counted |
|
if self._dim_k==0: |
|
if ind_i==ind_j: |
|
raise Exception("Do not use set_hop for onsite terms. Use set_onsite instead!") |
|
else: |
|
if ind_i==ind_j: |
|
all_zer=True |
|
for k in self._per: |
|
if int(ind_R[k])!=0: |
|
all_zer=False |
|
if all_zer==True: |
|
raise Exception("Do not use set_hop for onsite terms. Use set_onsite instead!") |
|
# |
|
# make sure that if <i|H|j+R> is specified that <j|H|i-R> is not! |
|
if allow_conjugate_pair==False: |
|
for h in self._hoppings: |
|
if ind_i==h[2] and ind_j==h[1]: |
|
if self._dim_k==0: |
|
raise Exception(\ |
|
"""Following matrix element was already implicitely specified: i="""+str(ind_i)+" j="+str(ind_j)+""" |
|
Remember, specifying <i|H|j> automatically specifies <j|H|i>. |
|
You need to specify only one of the two! If you know what you |
|
are doing and want to overrule this, see allow_conjugate_pair |
|
parameter in the documentation.""") |
|
elif False not in (np.array(ind_R)[self._per]==(-1)*np.array(h[3])[self._per]): |
|
raise Exception(\ |
|
"""Following matrix element was already implicitely specified: i="""+str(ind_i)+" j="+str(ind_j)+" R="+str(ind_R)+""" |
|
Remember, specifying <i|H|j+R> automatically specifies <j|H|i-R>. |
|
You need to specify only one of the two! If you know what you |
|
are doing and want to overrule this, see allow_conjugate_pair |
|
parameter in the documentation.""") |
|
# for of hopping term list to store |
|
if self._dim_k==0: |
|
new_hop=[hop_amp,int(ind_i),int(ind_j)] |
|
else: |
|
new_hop=[hop_amp,int(ind_i),int(ind_j),np.array(ind_R)] |
|
# |
|
# see if there is a hopping term with same i,j,R |
|
use_index=None |
|
for iih,h in enumerate(self._hoppings): |
|
# check if the same |
|
same_ijR=False |
|
if ind_i==h[1] and ind_j==h[2]: |
|
if self._dim_k==0: |
|
same_ijR=True |
|
else: |
|
if False not in (np.array(ind_R)[self._per]==np.array(h[3])[self._per]): |
|
same_ijR=True |
|
# if they are the same then store index of site at which they are the same |
|
if same_ijR==True: |
|
use_index=iih |
|
# |
|
# specifying hopping terms from scratch, can be called only once |
|
if mode.lower()=="set": |
|
# make sure we specify things only once |
|
if use_index!=None: |
|
raise Exception("Hopping energy for this site was already specified! Use mode=\"reset\" or mode=\"add\".") |
|
else: |
|
self._hoppings.append(new_hop) |
|
# reset value of hopping term, without adding to previous value |
|
elif mode.lower()=="reset": |
|
if use_index!=None: |
|
self._hoppings[use_index]=new_hop |
|
else: |
|
self._hoppings.append(new_hop) |
|
# add to previous value |
|
elif mode.lower()=="add": |
|
if use_index!=None: |
|
self._hoppings[use_index][0]+=new_hop[0] |
|
else: |
|
self._hoppings.append(new_hop) |
|
else: |
|
raise Exception("Wrong value of mode parameter") |
|
|
|
def display(self): |
|
r""" |
|
Prints on the screen some information about this tight-binding |
|
model. This function doesn't take any parameters. |
|
""" |
|
print '---------------------------------------' |
|
print 'report of tight-binding model' |
|
print '---------------------------------------' |
|
print 'k-space dimension =',self._dim_k |
|
print 'r-space dimension =',self._dim_r |
|
print 'periodic directions =',self._per |
|
print 'number of orbitals =',self._norb |
|
print 'lattice vectors:' |
|
for i,o in enumerate(self._lat): |
|
print " #",_nice_int(i,2)," ===> [", |
|
for j,v in enumerate(o): |
|
print _nice_float(v,7,4), |
|
if j!=len(o)-1: |
|
print ",", |
|
print "]" |
|
print 'positions of orbitals:' |
|
for i,o in enumerate(self._orb): |
|
print " #",_nice_int(i,2)," ===> [", |
|
for j,v in enumerate(o): |
|
print _nice_float(v,7,4), |
|
if j!=len(o)-1: |
|
print ",", |
|
print "]" |
|
print 'site energies:' |
|
for i,site in enumerate(self._site_energies): |
|
print " #",_nice_int(i,2)," ===> ", |
|
print _nice_float(site,7,4) |
|
print 'hoppings:' |
|
for i,hopping in enumerate(self._hoppings): |
|
print "<",_nice_int(hopping[1],2),"| H |",_nice_int(hopping[2],2), |
|
if len(hopping)==4: |
|
print "+ [", |
|
for j,v in enumerate(hopping[3]): |
|
print _nice_int(v,2), |
|
if j!=len(hopping[3])-1: |
|
print ",", |
|
else: |
|
print "]", |
|
print "> ===> ", |
|
print _nice_float(complex(hopping[0]).real,7,4), |
|
if complex(hopping[0]).imag<0.0: |
|
print " - ", |
|
else: |
|
print " + ", |
|
print _nice_float(abs(complex(hopping[0]).imag),7,4), |
|
print " i" |
|
print |
|
|
|
def visualize(self,dir_first,dir_second=None,eig_dr=None,draw_hoppings=True,ph_color="black"): |
|
r""" |
|
|
|
Rudimentary function for visualizing tight-binding model geometry, |
|
hopping between tight-binding orbitals, and electron eigenstates. |
|
|
|
If eigenvector is not drawn, then orbitals in home cell are drawn |
|
as red circles, and those in neighboring cells are drawn with |
|
different shade of red. Hopping term directions are drawn with |
|
green lines connecting two orbitals. Origin of unit cell is |
|
indicated with blue dot, while real space unit vectors are drawn |
|
with blue lines. |
|
|
|
If eigenvector is drawn, then electron eigenstate on each orbital |
|
is drawn with a circle whose size is proportional to wavefunction |
|
amplitude while its color depends on the phase. There are various |
|
coloring schemes for the phase factor; see more details under |
|
*ph_color* parameter. If eigenvector is drawn and coloring scheme |
|
is "red-blue" or "wheel", all other elements of the picture are |
|
drawn in gray or black. |
|
|
|
:param dir_first: First index of Cartesian coordinates used for |
|
plotting. |
|
|
|
:param dir_second: Second index of Cartesian coordinates used for |
|
plotting. For example if dir_first=0 and dir_second=2, and |
|
Cartesian coordinates of some orbital is [2.0,4.0,6.0] then it |
|
will be drawn at coordinate [2.0,6.0]. If dimensionality of real |
|
space (*dim_r*) is zero or one then dir_second should not be |
|
specified. |
|
|
|
:param eig_dr: Optional parameter specifying eigenstate to |
|
plot. If specified, this should be one-dimensional array of |
|
complex numbers specifying wavefunction at each orbital in the |
|
tight-binding basis. If not specified, eigenstate is not drawn. |
|
|
|
:param draw_hoppings: Optional parameter specifying whether to |
|
draw all allowed hopping terms in the tight-binding |
|
model. Default value is True. |
|
|
|
:param ph_color: Optional parameter determining the way |
|
eigenvector phase factors are translated into color. Default |
|
value is "black". |
|
|
|
* "black" -- phase of eigenvectors are ignored and wavefunction |
|
is always colored in black. |
|
|
|
* "red-blue" -- zero phase is drawn red, while phases or pi or |
|
-pi are drawn blue. Phases in between are interpolated between |
|
red and blue. Some phase information is lost in this coloring |
|
becase phase of +phi and -phi have same color. |
|
|
|
* "wheel" -- each phase is given unique color. In steps of pi/3 |
|
starting from 0, colors are assigned (in increasing hue) as: |
|
red, yellow, green, cyan, blue, magenta, red. |
|
|
|
:returns: |
|
* **fig** -- Figure object from matplotlib.pyplot module |
|
that can be used to save the figure in PDF, EPS or similar |
|
format, for example using fig.savefig("name.pdf") command. |
|
* **ax** -- Axes object from matplotlib.pyplot module that can be |
|
used to tweak the plot, for example by adding a plot title |
|
ax.set_title("Title goes here"). |
|
|
|
Example usage:: |
|
|
|
# Draws x-y projection of tight-binding model |
|
# tweaks figure and saves it as a PDF. |
|
(fig, ax) = tb.visualize(0, 1) |
|
ax.set_title("Title goes here") |
|
fig.savefig("model.pdf") |
|
|
|
See also these examples: :ref:`edge-example`, |
|
:ref:`visualize-example`. |
|
|
|
""" |
|
|
|
# check that ph_color is correct |
|
if ph_color not in ["black","red-blue","wheel"]: |
|
raise Exception("Wrong value of ph_color parameter!") |
|
|
|
# check if dir_second had to be specified |
|
if dir_second==None and self._dim_r>1: |
|
raise Exception("Need to specify index of second coordinate for projection!") |
|
|
|
# start a new figure |
|
fig=pl.figure(figsize=[pl.rcParams["figure.figsize"][0], |
|
pl.rcParams["figure.figsize"][0]]) |
|
ax=fig.add_subplot(111, aspect='equal') |
|
|
|
def proj(v): |
|
"Project vector onto drawing plane" |
|
coord_x=v[dir_first] |
|
if dir_second==None: |
|
coord_y=0.0 |
|
else: |
|
coord_y=v[dir_second] |
|
return [coord_x,coord_y] |
|
|
|
def to_cart(red): |
|
"Convert reduced to Cartesian coordinates" |
|
return np.dot(red,self._lat) |
|
|
|
# define colors to be used in plotting everything |
|
# except eigenvectors |
|
if eig_dr==None or ph_color=="black": |
|
c_cell="b" |
|
c_orb="r" |
|
c_nei=[0.85,0.65,0.65] |
|
c_hop="g" |
|
else: |
|
c_cell=[0.4,0.4,0.4] |
|
c_orb=[0.0,0.0,0.0] |
|
c_nei=[0.6,0.6,0.6] |
|
c_hop=[0.0,0.0,0.0] |
|
# determine color scheme for eigenvectors |
|
def color_to_phase(ph): |
|
if ph_color=="black": |
|
return "k" |
|
if ph_color=="red-blue": |
|
ph=np.abs(ph/np.pi) |
|
return [1.0-ph,0.0,ph] |
|
if ph_color=="wheel": |
|
if ph<0.0: |
|
ph=ph+2.0*np.pi |
|
ph=6.0*ph/(2.0*np.pi) |
|
x_ph=1.0-np.abs(ph%2.0-1.0) |
|
if ph>=0.0 and ph<1.0: ret_col=[1.0 ,x_ph,0.0 ] |
|
if ph>=1.0 and ph<2.0: ret_col=[x_ph,1.0 ,0.0 ] |
|
if ph>=2.0 and ph<3.0: ret_col=[0.0 ,1.0 ,x_ph] |
|
if ph>=3.0 and ph<4.0: ret_col=[0.0 ,x_ph,1.0 ] |
|
if ph>=4.0 and ph<5.0: ret_col=[x_ph,0.0 ,1.0 ] |
|
if ph>=5.0 and ph<6.0: ret_col=[1.0 ,0.0 ,x_ph] |
|
return ret_col |
|
|
|
# draw origin |
|
ax.plot([0.0],[0.0],"o",c=c_cell,mec="w",mew=0.0,zorder=7,ms=4.5) |
|
|
|
# first draw unit cell vectors which are considered to be periodic |
|
for i in self._per: |
|
# pick a unit cell vector and project it down to the drawing plane |
|
vec=proj(self._lat[i]) |
|
ax.plot([0.0,vec[0]],[0.0,vec[1]],"-",c=c_cell,lw=1.5,zorder=7) |
|
|
|
# now draw all orbitals |
|
for i in range(self._norb): |
|
# find position of orbital in cartesian coordinates |
|
pos=to_cart(self._orb[i]) |
|
pos=proj(pos) |
|
ax.plot([pos[0]],[pos[1]],"o",c=c_orb,mec="w",mew=0.0,zorder=10,ms=4.0) |
|
|
|
# draw hopping terms |
|
if draw_hoppings==True: |
|
for h in self._hoppings: |
|
# draw both i->j+R and i-R->j hop |
|
for s in range(2): |
|
# get "from" and "to" coordinates |
|
pos_i=np.copy(self._orb[h[1]]) |
|
pos_j=np.copy(self._orb[h[2]]) |
|
# add also lattice vector if not 0-dim |
|
if self._dim_k!=0: |
|
if s==0: |
|
pos_j[self._per]=pos_j[self._per]+h[3][self._per] |
|
if s==1: |
|
pos_i[self._per]=pos_i[self._per]-h[3][self._per] |
|
# project down vector to the plane |
|
pos_i=np.array(proj(to_cart(pos_i))) |
|
pos_j=np.array(proj(to_cart(pos_j))) |
|
# add also one point in the middle to bend the curve |
|
prcnt=0.05 # bend always by this ammount |
|
pos_mid=(pos_i+pos_j)*0.5 |
|
dif=pos_j-pos_i # difference vector |
|
orth=np.array([dif[1],-1.0*dif[0]]) # orthogonal to difference vector |
|
orth=orth/np.sqrt(np.dot(orth,orth)) # normalize |
|
pos_mid=pos_mid+orth*prcnt*np.sqrt(np.dot(dif,dif)) # shift mid point in orthogonal direction |
|
# draw hopping |
|
all_pnts=np.array([pos_i,pos_mid,pos_j]).T |
|
ax.plot(all_pnts[0],all_pnts[1],"-",c=c_hop,lw=0.75,zorder=8) |
|
# draw "from" and "to" sites |
|
ax.plot([pos_i[0]],[pos_i[1]],"o",c=c_nei,zorder=9,mew=0.0,ms=4.0,mec="w") |
|
ax.plot([pos_j[0]],[pos_j[1]],"o",c=c_nei,zorder=9,mew=0.0,ms=4.0,mec="w") |
|
|
|
# now draw the eigenstate |
|
if eig_dr!=None: |
|
for i in range(self._norb): |
|
# find position of orbital in cartesian coordinates |
|
pos=to_cart(self._orb[i]) |
|
pos=proj(pos) |
|
# find norm of eigenfunction at this point |
|
nrm=(eig_dr[i]*eig_dr[i].conjugate()).real |
|
# rescale and get size of circle |
|
nrm_rad=2.0*nrm*float(self._norb) |
|
# get color based on the phase of the eigenstate |
|
phase=np.angle(eig_dr[i]) |
|
c_ph=color_to_phase(phase) |
|
ax.plot([pos[0]],[pos[1]],"o",c=c_ph,mec="w",mew=0.0,ms=nrm_rad,zorder=11,alpha=0.8) |
|
|
|
# center the image |
|
# first get the current limit, which is probably tight |
|
xl=ax.set_xlim() |
|
yl=ax.set_ylim() |
|
# now get the center of current limit |
|
centx=(xl[1]+xl[0])*0.5 |
|
centy=(yl[1]+yl[0])*0.5 |
|
# now get the maximal size (lengthwise or heightwise) |
|
mx=max([xl[1]-xl[0],yl[1]-yl[0]]) |
|
# set new limits |
|
extr=0.05 # add some boundary as well |
|
ax.set_xlim(centx-mx*(0.5+extr),centx+mx*(0.5+extr)) |
|
ax.set_ylim(centy-mx*(0.5+extr),centy+mx*(0.5+extr)) |
|
|
|
# return a figure and axes to the user |
|
return (fig,ax) |
|
|
|
def get_num_orbitals(self): |
|
"Returns number of orbitals in the model." |
|
return self._norb |
|
|
|
def _gen_ham(self,k_input=None): |
|
"""Generate Hamiltonian for a certain k-point, |
|
K-point is given in reduced coordinates!""" |
|
kpnt=np.array(k_input) |
|
if k_input!=None: |
|
# if kpnt is just a number then convert it to an array |
|
if len(kpnt.shape)==0: |
|
kpnt=np.array([kpnt]) |
|
# check that k-vector is of corect size |
|
if kpnt.shape!=(self._dim_k,): |
|
raise Exception("k-vector of wrong shape!") |
|
else: |
|
if self._dim_k!=0: |
|
raise Exception("Have to provide a k-vector!") |
|
# zero the Hamiltonian matrix |
|
ham=np.zeros((self._norb,self._norb),dtype=complex) |
|
# modify diagonal elements |
|
for i in range(self._norb): |
|
ham[i,i]=self._site_energies[i] |
|
# go over all hoppings |
|
for hopping in self._hoppings: |
|
# get all data for the hopping parameter |
|
amp=complex(hopping[0]) |
|
i=hopping[1] |
|
j=hopping[2] |
|
# in 0-dim case there is no phase factor |
|
if self._dim_k>0: |
|
ind_R=np.array(hopping[3],dtype=float) |
|
# vector from one site to another |
|
rv=-self._orb[i,:]+self._orb[j,:]+ind_R |
|
# Take only components of vector which are periodic |
|
rv=rv[self._per] |
|
# Calculate the hopping, see details in info/tb/tb.pdf |
|
phase=np.exp((2.0j)*np.pi*np.dot(kpnt,rv)) |
|
amp=amp*phase |
|
# add this hopping into a matrix and also its conjugate |
|
ham[i,j]+=amp |
|
ham[j,i]+=amp.conjugate() |
|
self._ham = ham |
|
return ham |
|
|
|
def _sol_ham(self,ham,eig_vectors=False): |
|
"""Solves Hamiltonian and returns eigenvectors, eigenvalues""" |
|
#solve matrix |
|
if eig_vectors==False: # only find eigenvalues |
|
eval=np.linalg.eigvalsh(ham) |
|
# sort eigenvalues and convert to real numbers |
|
eval=_nicefy_eig(eval) |
|
return np.array(eval,dtype=float) |
|
else: # find eigenvalues and eigenvectors |
|
(eval,eig)=np.linalg.eigh(ham) |
|
# transpose matrix eig since otherwise it is confusing |
|
# now eig[i,:] is eigenvector for eval[i]-th eigenvalue |
|
eig=eig.T |
|
# sort evectors, eigenvalues and convert to real numbers |
|
(eval,eig)=_nicefy_eig(eval,eig) |
|
return (eval,eig) |
|
|
|
def solve_all(self,k_list=None,eig_vectors=False): |
|
r""" |
|
Solves for eigenvalues and (optionally) eigenvectors of the |
|
tight-binding model on a given one-dimensional list of k-vectors. |
|
|
|
.. note:: |
|
|
|
Eigenvectors (wavefunctions) returned by this |
|
function and used throughout the code are exclusively given |
|
in convention 1 as described in section 3.1 of |
|
:download:`notes on tight-binding formalism |
|
<misc/pythtb-formalism.pdf>`. In other words, they |
|
are in correspondence with cell-periodic functions |
|
:math:`u_{n {\bf k}} ({\bf r})` not |
|
:math:`\Psi_{n {\bf k}} ({\bf r})`. |
|
|
|
.. note:: |
|
|
|
In some cases class :class:`pythtb.wf_array` provides a more |
|
elegant way to deal with eigensolutions on a regular mesh of |
|
k-vectors. |
|
|
|
:param k_list: One-dimensional array of k-vectors. Each k-vector |
|
is given in reduced coordinates of the reciprocal space unit |
|
cell. For example, for real space unit cell vectors [1.0,0.0] |
|
and [0.0,2.0] and associated reciprocal space unit vectors |
|
[2.0*pi,0.0] and [0.0,pi], k-vector with reduced coordinates |
|
[0.25,0.25] corresponds to k-vector [0.5*pi,0.25*pi]. |
|
Dimensionalty of each vector must equal to the number of |
|
periodic directions (i.e. dimensionality of reciprocal space, |
|
*dim_k*). |
|
This parameter shouldn't be specified for system with |
|
zero-dimensional k-space (*dim_k* =0). |
|
|
|
:param eig_vectors: Optional boolean parameter, specifying whether |
|
eigenvectors should be returned. If *eig_vectors* is True, then |
|
both eigenvalues and eigenvectors are returned, otherwise only |
|
eigenvalues are returned. |
|
|
|
:returns: |
|
* **eval** -- Two dimensional array of eigenvalues for |
|
all bands for all kpoints. Format is eval[band,kpoint] where |
|
first index (band) corresponds to the electron band in |
|
question and second index (kpoint) corresponds to the k-point |
|
as listed in the input parameter *k_list*. Eigenvalues are |
|
sorted from smallest to largest at each k-point seperately. |
|
|
|
In the case when reciprocal space is zero-dimensional (as in a |
|
molecule) kpoint index is dropped and *eval* is of the format |
|
eval[band]. |
|
|
|
* **evec** -- Three dimensional array of eigenvectors for all |
|
bands and all kpoints. Format is evec[band,kpoint,orbital] |
|
where "band" is the electron band in question, "kpoint" is |
|
index of k-vector as given in input parameter |
|
*k_list*. Finally, "orbital" refers to the tight-binding |
|
orbital basis function. Ordering of bands is the same as in |
|
*eval*. |
|
|
|
Eigenvectors evec[n,k,j] correspond to :math:`C^{n {\bf |
|
k}}_{j}` from section 3.1 equation 3.5 and 3.7 of the |
|
:download:`notes on tight-binding formalism |
|
<misc/pythtb-formalism.pdf>`. |
|
|
|
In the case when reciprocal space is zero-dimensional (as in a |
|
molecule) kpoint index is dropped and *evec* is of the format |
|
evec[band,orbital]. |
|
|
|
Example usage:: |
|
|
|
# Returns eigenvalues for three k-vectors |
|
eval = tb.solve_all([[0.0, 0.0], [0.0, 0.2], [0.0, 0.5]]) |
|
# Returns eigenvalues and eigenvectors for two k-vectors |
|
(eval, evec) = tb.solve_all([[0.0, 0.0], [0.0, 0.2]], eig_vectors=True) |
|
|
|
""" |
|
# if not 0-dim case |
|
if not (k_list==None): |
|
nkp=len(k_list) # number of k points |
|
# first initialize matrices for all return data |
|
# indices are [band,kpoint] |
|
ret_eval=np.zeros((self._norb,nkp),dtype=float) |
|
# indices are [band,kpoint,orbital] |
|
ret_evec=np.zeros((self._norb,nkp,self._norb),dtype=complex) |
|
# go over all kpoints |
|
for i,k in enumerate(k_list): |
|
# generate Hamiltonian at that point |
|
ham=self._gen_ham(k) |
|
# solve Hamiltonian |
|
if eig_vectors==False: |
|
eval=self._sol_ham(ham,eig_vectors=eig_vectors) |
|
ret_eval[:,i]=eval[:] |
|
else: |
|
(eval,evec)=self._sol_ham(ham,eig_vectors=eig_vectors) |
|
ret_eval[:,i]=eval[:] |
|
ret_evec[:,i,:]=evec[:,:] |
|
# return stuff |
|
if eig_vectors==False: |
|
# indices of eval are [band,kpoint] |
|
return ret_eval |
|
else: |
|
# indices of eval are [band,kpoint] for evec are [band,kpoint,orbital] |
|
return (ret_eval,ret_evec) |
|
else: # 0 dim case |
|
# generate Hamiltonian |
|
ham=self._gen_ham() |
|
# solve |
|
if eig_vectors==False: |
|
eval=self._sol_ham(ham,eig_vectors=eig_vectors) |
|
# indices of eval are [band] |
|
return eval |
|
else: |
|
(eval,evec)=self._sol_ham(ham,eig_vectors=eig_vectors) |
|
# indices of eval are [band] and of evec are [band,orbital] |
|
return (eval,evec) |
|
|
|
def solve_one(self,k_point=None,eig_vectors=False): |
|
r""" |
|
|
|
Similar to :func:`pythtb.tb_model.solve_all` but solves tight-binding |
|
model for only one k-vector. |
|
|
|
""" |
|
# if not 0-dim case |
|
if k_point!=None: |
|
if eig_vectors==False: |
|
eval=self.solve_all([k_point],eig_vectors=eig_vectors) |
|
# indices of eval are [band] |
|
return eval[:,0] |
|
else: |
|
(eval,evec)=self.solve_all([k_point],eig_vectors=eig_vectors) |
|
# indices of eval are [band] for evec are [band,orbital] |
|
return (eval[:,0],evec[:,0,:]) |
|
else: |
|
# do the same as solve_all |
|
return self.solve_all(eig_vectors=eig_vectors) |
|
|
|
def cut_piece(self,num,fin_dir,glue_edgs=False): |
|
r""" |
|
Constructs a (d-1)-dimensional tight-binding model out of a |
|
d-dimensional one by repeating the unit cell a given number of |
|
times along one of the periodic lattice vectors. The real-space |
|
lattice vectors of the returned model are the same as those of |
|
the original model; only the dimensionality of reciprocal space |
|
is reduced. |
|
|
|
:param num: How many times to repeat the unit cell. |
|
|
|
:param fin_dir: Index of the real space lattice vector along |
|
which you no longer wish to maintain periodicity. |
|
|
|
:param glue_edgs: Optional boolean parameter specifying whether to |
|
allow hoppings from one edge to the other of a cut model. |
|
|
|
:returns: |
|
* **fin_model** -- Object of type |
|
:class:`pythtb.tb_model` representing a cutout |
|
tight-binding model. Orbitals in *fin_model* are |
|
numbered so that the i-th orbital of the n-th unit |
|
cell has index i+norb*n (here norb is the number of |
|
orbitals in the original model). |
|
|
|
Example usage:: |
|
|
|
A = tb_model(3, 3, ...) |
|
# Construct two-dimensional model B out of three-dimensional |
|
# model A by repeating model along second lattice vector ten times |
|
B = A.cut_piece(10, 1) |
|
# Further cut two-dimensional model B into one-dimensional model |
|
# A by repeating unit cell twenty times along third lattice |
|
# vector and allow hoppings from one edge to the other |
|
C = B.cut_piece(20, 2, glue_edgs=True) |
|
|
|
See also these examples: :ref:`haldane_fin-example`, |
|
:ref:`edge-example`. |
|
|
|
|
|
""" |
|
if self._dim_k ==0: |
|
raise Exception("Model is already finite") |
|
if type(num).__name__!='int': |
|
raise Exception("Argument num not an integer") |
|
|
|
# generate orbitals of a finite model |
|
fin_orb=[] |
|
onsite=[] # store also onsite energies |
|
for i in range(num): # go over all cells in finite direction |
|
for j in range(self._norb): # go over all orbitals in one cell |
|
# make a copy of j-th orbital |
|
orb_tmp=np.copy(self._orb[j,:]) |
|
# change coordinate along finite direction |
|
orb_tmp[fin_dir]+=float(i) |
|
# add to the list |
|
fin_orb.append(orb_tmp) |
|
# do the onsite energies at the same time |
|
onsite.append(self._site_energies[j]) |
|
fin_orb=np.array(fin_orb) |
|
|
|
# generate periodic directions of a finite model |
|
fin_per=copy.deepcopy(self._per) |
|
# find if list of periodic directions contains the one you |
|
# want to make finite |
|
if fin_per.count(fin_dir)!=1: |
|
raise Exception("Can not make model finite along this direction!") |
|
# remove index which is no longer periodic |
|
fin_per.remove(fin_dir) |
|
|
|
# generate object of tb_model type that will correspond to a cutout |
|
fin_model=tb_model(self._dim_k-1, |
|
self._dim_r, |
|
copy.deepcopy(self._lat), |
|
fin_orb, |
|
fin_per) |
|
|
|
# now put all onsite terms for the finite model |
|
fin_model.set_onsite(onsite,mode="reset") |
|
|
|
# put all hopping terms |
|
for c in range(num): # go over all cells in finite direction |
|
for h in range(len(self._hoppings)): # go over all hoppings in one cell |
|
# amplitude of the hop is the same |
|
amp=self._hoppings[h][0] |
|
|
|
# lattice vector of the hopping |
|
ind_R=copy.deepcopy(self._hoppings[h][3]) |
|
jump_fin=ind_R[fin_dir] # store by how many cells is the hopping in finite direction |
|
if fin_model._dim_k!=0: |
|
ind_R[fin_dir]=0 # one of the directions now becomes finite |
|
|
|
# index of "from" and "to" hopping indices |
|
hi=self._hoppings[h][1] + c*self._norb |
|
# have to compensate for the fact that ind_R in finite direction |
|
# will not be used in the finite model |
|
hj=self._hoppings[h][2] + (c + jump_fin)*self._norb |
|
|
|
# decide whether this hopping should be added or not |
|
to_add=True |
|
# if edges are not glued then neglect all jumps that spill out |
|
if glue_edgs==False: |
|
if hj<0 or hj>=self._norb*num: |
|
to_add=False |
|
# if edges are glued then do mod division to wrap up the hopping |
|
else: |
|
hj=int(hj)%int(self._norb*num) |
|
|
|
# add hopping to a finite model |
|
if to_add==True: |
|
if fin_model._dim_k==0: |
|
fin_model.set_hop(amp,hi,hj,mode="add",allow_conjugate_pair=True) |
|
else: |
|
fin_model.set_hop(amp,hi,hj,ind_R,mode="add",allow_conjugate_pair=True) |
|
|
|
return fin_model |
|
|
|
def reduce_dim(self,remove_k,value_k): |
|
r""" |
|
Reduces dimensionality of the model by taking a reciprocal-space |
|
slice of the Bloch Hamiltonian :math:`{\cal H}_{\bf k}`. The Bloch |
|
Hamiltonian (defined in :download:`notes on tight-binding |
|
formalism <misc/pythtb-formalism.pdf>` in section 3.1 equation 3.7) of a |
|
d-dimensional model is a function of d-dimensional k-vector. |
|
|
|
This function returns a d-1 dimensional tight-binding model obtained |
|
by constraining one of k-vector components in :math:`{\cal H}_{\bf |
|
k}` to be a constant. |
|
|
|
:param remove_k: Which reciprocal space unit vector component |
|
you wish to keep constant. |
|
|
|
:param value_k: Value of the k-vector component to which you are |
|
constraining this model. Must be given in reduced coordinates. |
|
|
|
:returns: |
|
* **red_tb** -- Object of type :class:`pythtb.tb_model` |
|
representing a reduced tight-binding model. |
|
|
|
Example usage:: |
|
|
|
# Constrains second k-vector component to equal 0.3 |
|
red_tb = tb.reduce_dim(1, 0.3) |
|
|
|
""" |
|
# |
|
if self._dim_k==0: |
|
raise Exception("Can not reduce dimensionality even further!") |
|
# make a copy |
|
red_tb=copy.deepcopy(self) |
|
# make one of the directions not periodic |
|
red_tb._per.remove(remove_k) |
|
red_tb._dim_k=len(red_tb._per) |
|
# check that really removed one and only one direction |
|
if red_tb._dim_k!=self._dim_k-1: |
|
raise Exception("Specified wrong dimension to reduce!") |
|
# modify all hopping parameters for this value of value_k |
|
for h in range(len(self._hoppings)): |
|
hop=self._hoppings[h] |
|
amp=complex(hop[0]) |
|
i=hop[1]; j=hop[2] |
|
ind_R=np.array(hop[3],dtype=float) |
|
# vector from one site to another |
|
rv=-red_tb._orb[i,:]+red_tb._orb[j,:]+ind_R |
|
# take only r-vector component along direction you are not making periodic |
|
rv=rv[remove_k] |
|
# Calculate the part of hopping phase, only for this direction |
|
phase=np.exp((2.0j)*np.pi*(value_k*rv)) |
|
red_tb._hoppings[h][0]=amp*phase |
|
return red_tb |
|
|
|
# keeping old name for backwards compatibility |
|
# will be removed in future |
|
tb_model.set_sites=tb_model.set_onsite |
|
tb_model.add_hop=tb_model.set_hop |
|
tbmodel=tb_model |
|
|
|
class wf_array: |
|
r""" |
|
|
|
This class is used to solve a tight-binding model |
|
:class:`pythtb.tb_model` on a regular or non-regular grid of points in |
|
reciprocal space and perform on it various calculations. For example |
|
it can be used to calculate the Berry phase, Berry curvature, |
|
1st Chern number, etc. |
|
|
|
Regular grid of points can be generated using function |
|
:func:`pythtb.wf_array.solve_on_grid` which will populate array |
|
with wavefunctions (eigenvectors) at a regular grid of points in |
|
the Brillouin zone, covering entire zone uniformly. |
|
|
|
Irregular grid of points can be populated manually with the help |
|
of *[]* operator. For example, to set eigenvectors *evec* to |
|
coordinate (2,3) in the *wf_array* object *wf* one can simply do:: |
|
|
|
wf[2,3]=evec |
|
|
|
Format of eigenvectors (wavefunctions) *evec* in example above is |
|
expected to be of the format *evec[band,orbital]*. This is the |
|
same format as returned by :func:`pythtb.tb_model.solve_one` or |
|
:func:`pythtb.tb_model.solve_all` (in this later case one needs to |
|
restrict it to a single k-point as *evec[:,kpt,:]* if model has |
|
*dim_k>=1*). |
|
|
|
Example :ref:`haldane_bp-example` shows how to use wf_array on |
|
regular grid of points in k-space. Examples :ref:`cone-example` |
|
and :ref:`lambda-example` show how to use non-regular grid of |
|
points. In particular, example :ref:`lambda-example` shows how one |
|
of the directions of *wf_array* object needs not be k-vector |
|
direction but it can be some Hamiltonian parameter :math:`\lambda` |
|
(see also discussion after equation 4.1 in :download:`notes on |
|
tight-binding formalism <misc/pythtb-formalism.pdf>`). |
|
|
|
If wf_array is used for closed paths in reciprocal space (either |
|
across the boundary of Brillouin zone or not) then one needs to |
|
specify both starting and ending eigenfunctions (eventhough they |
|
correspond physically to the same or equivalent point in reciprocal |
|
space). |
|
|
|
:param model: Object of type :class:`pythtb.tb_model` representing |
|
tight-binding model associated with this array of eigenvectors. |
|
|
|
:param mesh_arr: Array giving a dimension of the grid of points in |
|
reciprocal space in each direction. |
|
|
|
Example usage:: |
|
|
|
# Construct wf_array capable of storing 10x20 array of |
|
# wavefunctions |
|
wf = wf_array(tb, [10, 20]) |
|
# populate this wf_array with regular grid of points in |
|
# Brillouin zone |
|
wf.solve_on_grid([0.0, 0.0]) |
|
|
|
# Compute set of eigenvectors at one k-point |
|
(eval, evec) = tb.solve_one([kx, ky], eig_vectors = True) |
|
# Store manually eigenvector evec at given place in the array |
|
wf[3, 4] = evec |
|
# To access eigenvector from the same position |
|
print wf[3, 4] |
|
|
|
""" |
|
def __init__(self,model,mesh_arr): |
|
# store orbitals from the model |
|
self._norb=model._norb |
|
self._orb=np.copy(model._orb) |
|
# store entire model as well |
|
self._model=copy.deepcopy(model) |
|
# store dimension of array of points on which to keep wavefunctions |
|
self._mesh_arr=np.array(mesh_arr) |
|
self._dim_arr=len(self._mesh_arr) |
|
# generate temporary array used later to generate object ._wfs |
|
wfs_dim=np.copy(self._mesh_arr) |
|
wfs_dim=np.append(wfs_dim,self._norb) |
|
wfs_dim=np.append(wfs_dim,self._norb) |
|
# store wavefunctions here in the form _wfs[kx_index,ky_index, ... ,band,orb] |
|
self._wfs=np.zeros(wfs_dim,dtype=complex) |
|
|
|
def solve_on_grid(self,start_k): |
|
r""" |
|
|
|
Solve a tight-binding model on a regular mesh of k-points covering |
|
the entire reciprocal-space unit cell. Both points at the opposite |
|
sides of reciprocal-space unit cell are included in the array. |
|
|
|
This function also imposes automatically periodic boundary |
|
conditions on the eigenfunctions. See also the discussion in |
|
:func:`pythtb.wf_array.impose_pbc`. |
|
|
|
:param start_k: Anchoring point of a regular grid of points in |
|
reciprocal space. |
|
|
|
Example usage:: |
|
|
|
# Solve eigenvectors on a regular grid anchored |
|
# at a given point |
|
wf.solve_on_grid([-0.5, -0.5]) |
|
|
|
""" |
|
# check dimensionality |
|
if self._dim_arr!=self._model._dim_k: |
|
raise Exception("If using solve_on_grid method, dimension of wf_array must equal dim_k of the tight-binding model!") |
|
# |
|
if self._dim_arr==1: |
|
for i in range(self._mesh_arr[0]): |
|
# generate a kpoint |
|
kpt=[start_k[0]+float(i)/float(self._mesh_arr[0]-1)] |
|
# solve at that point |
|
(eval,evec)=self._model.solve_one(kpt,eig_vectors=True) |
|
# store wavefunctions |
|
self[i]=evec |
|
# impose boundary conditions |
|
self.impose_pbc(0,self._model._per[0]) |
|
elif self._dim_arr==2: |
|
for i in range(self._mesh_arr[0]): |
|
for j in range(self._mesh_arr[1]): |
|
kpt=[start_k[0]+float(i)/float(self._mesh_arr[0]-1),\ |
|
start_k[1]+float(j)/float(self._mesh_arr[1]-1)] |
|
(eval,evec)=self._model.solve_one(kpt,eig_vectors=True) |
|
self[i,j]=evec |
|
for dir in range(2): |
|
self.impose_pbc(dir,self._model._per[dir]) |
|
elif self._dim_arr==3: |
|
for i in range(self._mesh_arr[0]): |
|
for j in range(self._mesh_arr[1]): |
|
for k in range(self._mesh_arr[2]): |
|
kpt=[start_k[0]+float(i)/float(self._mesh_arr[0]-1),\ |
|
start_k[1]+float(j)/float(self._mesh_arr[1]-1),\ |
|
start_k[2]+float(k)/float(self._mesh_arr[2]-1)] |
|
(eval,evec)=self._model.solve_one(kpt,eig_vectors=True) |
|
self[i,j,k]=evec |
|
for dir in range(3): |
|
self.impose_pbc(dir,self._model._per[dir]) |
|
else: |
|
raise Exception("Wrong dimensionality!") |
|
|
|
def __check_key(self,key): |
|
# do some checks for 1D |
|
if self._dim_arr==1: |
|
if type(key).__name__!='int': |
|
raise TypeError("Key should be an integer!") |
|
if key<(-1)*self._mesh_arr[0] or key>=self._mesh_arr[0]: |
|
raise IndexError("Key outside the range!") |
|
# do checks for higher dimension |
|
else: |
|
if len(key)!=self._dim_arr: |
|
raise TypeError("Wrong dimensionality of key!") |
|
for i,k in enumerate(key): |
|
if type(k).__name__!='int': |
|
raise TypeError("Key should be set of integers!") |
|
if k<(-1)*self._mesh_arr[i] or k>=self._mesh_arr[i]: |
|
raise IndexError("Key outside the range!") |
|
|
|
def __getitem__(self,key): |
|
# check that key is in the correct range |
|
self.__check_key(key) |
|
# return wavefunction |
|
return self._wfs[key] |
|
|
|
def __setitem__(self,key,value): |
|
# check that key is in the correct range |
|
self.__check_key(key) |
|
# store wavefunction |
|
self._wfs[key]=np.array(value,dtype=complex) |
|
|
|
def impose_pbc(self,mesh_dir,k_dir): |
|
r""" |
|
|
|
If *wf_array* object was populated using the |
|
:func:`pythtb.wf_array.solve_on_grid` method, this function |
|
should not be used since it will be called automatically by |
|
the code. |
|
|
|
The Bloch Hamiltonian :math:`{\cal H}_{\bf k}` is a periodic |
|
function of the k-vector. The eigenfunctions :math:`\Psi_{n |
|
{\bf k}}` are by convention choosen so that they are also |
|
periodic in k-vector (without phase factors). For this reason, |
|
the cell-periodic functions :math:`u_{n {\bf k}}` need to aquire |
|
a phase factor as one goes across the Brillouin zone. |
|
|
|
See :download:`notes on tight-binding formalism |
|
<misc/pythtb-formalism.pdf>` section 4.4 and equation 4.18 for |
|
more detail. |
|
|
|
This function will impose periodic boundary conditions along |
|
one direction of array. We are assuming that the k-point mesh |
|
increases by exactly one reciprocal lattice vector along this |
|
direction. This is currently **not** checked by the code, and |
|
is responsibility of the user. Currently *wf_array* does not |
|
store the k-vectors on which the model was solved, it only |
|
stores eigenvectors (wavefunctions). |
|
|
|
:param mesh_dir: Direction of wf_array along which you wish to |
|
impose periodic boundary condition. |
|
|
|
:param k_dir: Corresponding (to *mesh_dir*) direction in the |
|
Brillouin zone of underlying *tb_model*. |
|
|
|
See example :ref:`lambda-example` where periodic boundary |
|
condition is applied only along one direction of *wf_array*. |
|
|
|
Example usage:: |
|
|
|
# Imposes periodic boundary conditions along mesh_dir=0 |
|
# direction of wf_array object, assuming that along that |
|
# direction k_dir=1 component of k-vector is increased by |
|
# one reciprocal lattice vector. This could happen for |
|
# example if underlying tb_model is two dimensional but |
|
# wf_array is one-dimensional path along k_y direction. |
|
wf.impose_pbc(mesh_dir=0,k_dir=1) |
|
|
|
""" |
|
|
|
# periodic direction in k-space along which we are imposing |
|
# boundary condition |
|
pbc_k=self._model._per[k_dir] |
|
|
|
# TODO: this part can be written in a nicer way |
|
# |
|
# Impose periodic boundary conditions on wavefunctions |
|
#= 1-D case |
|
if self._dim_arr==1: |
|
if mesh_dir not in [0]: |
|
raise Exception("Wrong value of mesh_dir.") |
|
if mesh_dir==0: |
|
for i in range(self._norb): |
|
self._wfs[-1,:,i]=self._wfs[0,:,i]*np.exp(-2.j*np.pi*self._orb[i][pbc_k]) |
|
#= 2-D case |
|
elif self._dim_arr==2: |
|
if mesh_dir not in [0,1]: |
|
raise Exception("Wrong value of mesh_dir.") |
|
if mesh_dir==0: |
|
for i in range(self._norb): |
|
self._wfs[-1,:,:,i]=self._wfs[0,:,:,i]*np.exp(-2.j*np.pi*self._orb[i][pbc_k]) |
|
if mesh_dir==1: |
|
for i in range(self._norb): |
|
self._wfs[:,-1,:,i]=self._wfs[:,0,:,i]*np.exp(-2.j*np.pi*self._orb[i][pbc_k]) |
|
#= 3-D case |
|
elif self._dim_arr==3: |
|
if mesh_dir not in [0,1,2]: |
|
raise Exception("Wrong value of mesh_dir.") |
|
if mesh_dir==0: |
|
for i in range(self._norb): |
|
self._wfs[-1,:,:,:,i]=self._wfs[0,:,:,:,i]*np.exp(-2.j*np.pi*self._orb[i][pbc_k]) |
|
if mesh_dir==1: |
|
for i in range(self._norb): |
|
self._wfs[:,-1,:,:,i]=self._wfs[:,0,:,:,i]*np.exp(-2.j*np.pi*self._orb[i][pbc_k]) |
|
if mesh_dir==2: |
|
for i in range(self._norb): |
|
self._wfs[:,:,-1,:,i]=self._wfs[:,:,0,:,i]*np.exp(-2.j*np.pi*self._orb[i][pbc_k]) |
|
else: |
|
raise Exception("Wrong dimensionality!") |
|
|
|
def berry_phase(self,occ,dir=None,contin=True,berry_evals=False): |
|
r""" |
|
|
|
Computes Berry phase along a given direction and for a given |
|
set of occupied states. This assumes that the occupied bands |
|
are well separated in energy from unoccupied bands. It is the |
|
responsibility of the user to check that this is satisfied. |
|
Optionally, return the phases of the individual eigenvalues of |
|
the product of overlap matrices (see parameter berry_evals for |
|
more details). |
|
|
|
For a one-dimensional wf_array (i.e., a single string), the |
|
computed Berry phases are always chosen to be between -pi and pi. |
|
|
|
For a higher dimensional wf_array, the Berry phase is computed |
|
for each one-dimensional string of points, and an array of |
|
Berry phases is returned. The Berry phase for the first string |
|
(with lowest index) is always constrained to be between -pi and |
|
pi. The range of the remaining phases depends on the value of |
|
the input parameter *contin*. |
|
|
|
Optionally, can return phases of individual eigenvalues of the |
|
product matrices, instead of the Berry phase. |
|
|
|
Discretized formula used to compute Berry phase is described |
|
in section 4.5 of :download:`notes on tight-binding formalism |
|
<misc/pythtb-formalism.pdf>`. |
|
|
|
:param occ: Array of indices of energy bands which are considered |
|
to be occupied. |
|
|
|
:param dir: Index of wf_array direction along which Berry phase is |
|
computed. This parameters needs not be specified for |
|
a one-dimensional wf_array. |
|
|
|
:param contin: Optional boolean parameter. If True then the |
|
branch choice of the Berry phase (which is indeterminate |
|
modulo 2*pi) is made so that neighboring strings (in the |
|
direction of increasing index value) have as close as |
|
possible phases. The phase of the first string (with lowest |
|
index) is always constrained to be between -pi and pi. If |
|
False, the Berry phase for every string is constrained to be |
|
between -pi and pi. The default value is True. |
|
|
|
:param berry_evals: Optional boolean parameter. If True then |
|
will compute and return the phases of the eigenvalues of the |
|
product of overlap matrices. (These numbers correspond also |
|
to hybrid Wannier function centers.) These phases are either |
|
forced to be between -pi and pi (if *contin* is *False*) or |
|
they are made to be continuous (if *contin* is True). |
|
|
|
:returns: |
|
* **pha** -- If *berry_evals* is False (default value) then |
|
returns the Berry phase for each string. For a |
|
one-dimensional wf_array this is just one number. For a |
|
higher-dimensional wf_array *pha* contains one phase for |
|
each one-dimensional string in the following format. For |
|
example, if *wf_array* contains k-points on mesh with |
|
indices [i,j,k] and if direction along which Berry phase |
|
is computed is *dir=1* then *pha* will be two dimensional |
|
array with indices [i,k], since Berry phase is computed |
|
along second direction. If *berry_evals* is True then for |
|
each string returns phases of all eigenvalues of the |
|
product of overlap matrices. In the convention used for |
|
previous example, *pha* in this case would have indices |
|
[i,k,n] where *n* refers to index of individual phase of |
|
the product matrix eigenvalue. |
|
|
|
Example usage:: |
|
|
|
# Computes Berry phases along second direction for three lowest |
|
# occupied states. For example, if wf is threedimensional, then |
|
# pha[2,3] would correspond to Berry phase of string of states |
|
# along wf[2,:,3] |
|
pha = wf.berry_phase([0, 1, 2], 1) |
|
|
|
See also these examples: :ref:`haldane_bp-example`, |
|
:ref:`cone-example`, :ref:`lambda-example`, |
|
|
|
""" |
|
|
|
#if dir<0 or dir>self._dim_arr-1: |
|
# raise Exception("Direction key out of range") |
|
# |
|
# This could be coded more efficiently, but it is hard-coded for now. |
|
# |
|
# 1D case |
|
if self._dim_arr==1: |
|
# pick which wavefunctions to use |
|
wf_use=self._wfs[:,occ,:] |
|
# calculate berry phase |
|
ret=_one_berry_loop(wf_use,berry_evals) |
|
# 2D case |
|
elif self._dim_arr==2: |
|
# choice along which direction you wish to calculate berry phase |
|
if dir==0: |
|
ret=[] |
|
for i in range(self._mesh_arr[1]): |
|
wf_use=self._wfs[:,i,:,:][:,occ,:] |
|
ret.append(_one_berry_loop(wf_use,berry_evals)) |
|
elif dir==1: |
|
ret=[] |
|
for i in range(self._mesh_arr[0]): |
|
wf_use=self._wfs[i,:,:,:][:,occ,:] |
|
ret.append(_one_berry_loop(wf_use,berry_evals)) |
|
else: |
|
raise Exception("Wrong direction for Berry phase calculation!") |
|
# 3D case |
|
elif self._dim_arr==3: |
|
# choice along which direction you wish to calculate berry phase |
|
if dir==0: |
|
ret=[] |
|
for i in range(self._mesh_arr[1]): |
|
ret_t=[] |
|
for j in range(self._mesh_arr[2]): |
|
wf_use=self._wfs[:,i,j,:,:][:,occ,:] |
|
ret_t.append(_one_berry_loop(wf_use,berry_evals)) |
|
ret.append(ret_t) |
|
elif dir==1: |
|
ret=[] |
|
for i in range(self._mesh_arr[0]): |
|
ret_t=[] |
|
for j in range(self._mesh_arr[2]): |
|
wf_use=self._wfs[i,:,j,:,:][:,occ,:] |
|
ret_t.append(_one_berry_loop(wf_use,berry_evals)) |
|
ret.append(ret_t) |
|
elif dir==2: |
|
ret=[] |
|
for i in range(self._mesh_arr[0]): |
|
ret_t=[] |
|
for j in range(self._mesh_arr[1]): |
|
wf_use=self._wfs[i,j,:,:,:][:,occ,:] |
|
ret_t.append(_one_berry_loop(wf_use,berry_evals)) |
|
ret.append(ret_t) |
|
else: |
|
raise Exception("Wrong direction for Berry phase calculation!") |
|
else: |
|
raise Exception("Wrong dimensionality!") |
|
|
|
# convert phases to numpy array |
|
if self._dim_arr>1 or berry_evals==True: |
|
ret=np.array(ret,dtype=float) |
|
|
|
# make phases of eigenvalues continuous |
|
if contin==True: |
|
# iron out 2pi jumps, make the gauge choice such that first phase in the |
|
# list is fixed, others are then made continuous. |
|
if berry_evals==False: |
|
# 2D case |
|
if self._dim_arr==2: |
|
ret=_one_phase_cont(ret,ret[0]) |
|
# 3D case |
|
elif self._dim_arr==3: |
|
for i in range(ret.shape[1]): |
|
if i==0: clos=ret[0,0] |
|
else: clos=ret[0,i-1] |
|
ret[:,i]=_one_phase_cont(ret[:,i],clos) |
|
elif self._dim_arr!=1: |
|
raise Exception("Wrong dimensionality!") |
|
# make eigenvalues continuous. This does not take care of band-character |
|
# at band crossing for example it will just connect pairs that are closest |
|
# at neighboring points. |
|
else: |
|
# 2D case |
|
if self._dim_arr==2: |
|
ret=_array_phases_cont(ret,ret[0,:]) |
|
# 3D case |
|
elif self._dim_arr==3: |
|
for i in range(ret.shape[1]): |
|
if i==0: clos=ret[0,0,:] |
|
else: clos=ret[0,i-1,:] |
|
ret[:,i]=_array_phases_cont(ret[:,i],clos) |
|
elif self._dim_arr!=1: |
|
raise Exception("Wrong dimensionality!") |
|
return ret |
|
|
|
def berry_curv(self,occ,individual_phases=False): |
|
r""" |
|
|
|
Calculates the integral of Berry curvature over a |
|
two-dimensional *wf_array* by computing Berry phase around |
|
each small plaquette in the array. |
|
|
|
Currently not implemented for higher dimensions. |
|
|
|
:param occ: Array of indices of energy bands which are considered |
|
to be occupied. |
|
|
|
:param individual_phases: If *True* then returns Berry phase |
|
for each plaquette in the array. Default value is *False*. |
|
|
|
:returns: |
|
|
|
* **curv** -- Integral of Berry curvature. If |
|
*individual_phases* is *True* then returns integral of |
|
Berry curvature for each plaquette. |
|
|
|
Example usage:: |
|
|
|
# Computes integral of Berry curvature of first three bands |
|
curv = wf.berry_curv([0, 1, 2]) |
|
|
|
""" |
|
# 2D case |
|
if self._dim_arr==2: |
|
if individual_phases==False: |
|
curv=0.0 |
|
else: |
|
all_phases=np.zeros((self._mesh_arr[0]-1,self._mesh_arr[1]-1),dtype=float) |
|
# sum over all small squares |
|
for i in range(self._mesh_arr[0]-1): |
|
for j in range(self._mesh_arr[1]-1): |
|
# generate a small loop made out of four pieces |
|
wf_use=np.zeros((5,len(occ),self._wfs.shape[-1]),dtype=complex) |
|
wf_use[0]=self._wfs[i,j,:,:][occ,:] |
|
wf_use[1]=self._wfs[i+1,j,:,:][occ,:] |
|
wf_use[2]=self._wfs[i+1,j+1,:,:][occ,:] |
|
wf_use[3]=self._wfs[i,j+1,:,:][occ,:] |
|
wf_use[4]=self._wfs[i,j,:,:][occ,:] |
|
# calculate phase around one square |
|
one_phase=_one_berry_loop(wf_use) |
|
# sum up phases |
|
if individual_phases==False: |
|
curv+=one_phase |
|
# or store each individual phase |
|
else: |
|
all_phases[i,j]=one_phase |
|
|
|
else: |
|
raise Exception("Wrong dimensionality!") |
|
|
|
if individual_phases==False: |
|
return curv |
|
else: |
|
return all_phases |
|
|
|
def k_path(kpts,nk,endpoint=True): |
|
r""" |
|
|
|
Interpolates a path in reciprocal space between specified |
|
k-points. |
|
|
|
.. note:: The reciprocal-space path returned by this function can be |
|
used in a function call to :func:`pythtb.tb_model.solve_all`. See |
|
example below. |
|
|
|
:param kpts: Array of k-vectors in reciprocal space between which |
|
interpolation should be constructed. These k-vectors have to be |
|
given in reduced coordinates. |
|
|
|
:param nk: Number of k-points used in interpolation between two |
|
neighboring k-vectors. |
|
|
|
:param endpoint: If True (default) then last point given in kpts |
|
is explicitly included in the path. |
|
|
|
:returns: |
|
* **kpts** -- Array of interpolated k-vectors. |
|
|
|
Example usage:: |
|
|
|
# Constructs a path between four special points in reciprocal |
|
# space and solve for eigenvalues on that path |
|
path = [[0.0, 0.0], [0.0, 0.5], [0.5, 0.5], [0.0, 0.0]] |
|
kpts = k_path(path, 100) |
|
evals = tb.solve_all(kpts) |
|
|
|
""" |
|
if kpts=='full': |
|
# this means the full Brillouin zone for 1D case |
|
if endpoint==True: |
|
return np.array(range(nk+1),dtype=float)/nk |
|
else: |
|
return np.array(range(nk),dtype=float)/nk |
|
elif kpts=='half': |
|
# this means the half Brillouin zone for 1D case |
|
if endpoint==True: |
|
return np.array(range(nk+1),dtype=float)/(2*nk) |
|
else: |
|
return np.array(range(nk),dtype=float)/(2*nk) |
|
else: |
|
# general case |
|
kint=[] |
|
k_list=np.array(kpts) |
|
# go over all kpoints |
|
for i in range(len(k_list)-1): |
|
# go over all steps |
|
for j in range(nk): |
|
cur=k_list[i]+(k_list[i+1]-k_list[i])*float(j)/float(nk) |
|
kint.append(cur) |
|
# add last point |
|
if endpoint==True: |
|
kint.append(k_list[-1]) |
|
# |
|
kint=np.array(kint) |
|
return kint |
|
|
|
def _nicefy_eig(eval,eig=None): |
|
"Sort eigenvaules and eigenvectors, if given, and convert to real numbers" |
|
# first take only real parts of the eigenvalues |
|
eval=np.array(eval.real,dtype=float) |
|
# sort energies |
|
args=eval.argsort() |
|
eval=eval[args] |
|
if eig!=None: |
|
eig=eig[args] |
|
return (eval,eig) |
|
return eval |
|
|
|
# for nice justified printout |
|
def _nice_float(x,just,rnd): |
|
return str(round(x,rnd)).rjust(just) |
|
def _nice_int(x,just): |
|
return str(x).rjust(just) |
|
|
|
def _wf_dpr(wf1,wf2): |
|
"""calculate dot product between two wavefunctions. |
|
wf1 and wf2 are of the form [orbital]""" |
|
return np.dot(wf1.conjugate(),wf2) |
|
|
|
def _one_berry_loop(wf,berry_evals=False): |
|
"""Do one Berry phase calculation (also returns a product of M |
|
matrices). Always returns numbers between -pi and pi. wf has |
|
format [kpnt,band,orbital] and kpnt has to be one dimensional. |
|
Assumes that first and last k-point are the same. Therefore if |
|
there are n wavefunctions in total, will calculate phase along n-1 |
|
links only! If berry_evals is True then will compute phases for |
|
individual states, these corresponds to 1d hybrid Wannier |
|
function centers. Otherwise just return one number, Berry phase.""" |
|
# number of occupied states |
|
nocc=wf.shape[1] |
|
# temporary matrices |
|
prd=np.identity(nocc,dtype=complex) |
|
ovr=np.zeros([nocc,nocc],dtype=complex) |
|
# go over all pairs of k-points, assuming that last point is overcounted! |
|
for i in range(wf.shape[0]-1): |
|
# generate overlap matrix, go over all bands |
|
for j in range(nocc): |
|
for k in range(nocc): |
|
ovr[j,k]=_wf_dpr(wf[i,j,:],wf[i+1,k,:]) |
|
# only find Berry phase |
|
if berry_evals==False: |
|
# multiply overlap matrices |
|
prd=np.dot(prd,ovr) |
|
# also find phases of individual eigenvalues |
|
else: |
|
# cleanup matrices with SVD then take product |
|
matU,sing,matV=np.linalg.svd(ovr) |
|
prd=np.dot(prd,np.dot(matU,matV)) |
|
# calculate Berry phase |
|
if berry_evals==False: |
|
det=np.linalg.det(prd) |
|
pha=(-1.0)*np.angle(det) |
|
return pha |
|
# calculate phases of all eigenvalues |
|
else: |
|
evals=np.linalg.eigvals(prd) |
|
eval_pha=(-1.0)*np.angle(evals) |
|
# sort these numbers as well |
|
eval_pha=np.sort(eval_pha) |
|
return eval_pha |
|
|
|
def no_2pi(x,clos): |
|
"Make x as close to clos by adding or removing 2pi" |
|
while abs(clos-x)>np.pi: |
|
if clos-x>np.pi: |
|
x+=2.0*np.pi |
|
elif clos-x<-1.0*np.pi: |
|
x-=2.0*np.pi |
|
return x |
|
|
|
def _one_phase_cont(pha,clos): |
|
"""Reads in 1d array of numbers *pha* and makes sure that they are |
|
continuous, i.e., that there are no jumps of 2pi. First number is |
|
made as close to *clos* as possible.""" |
|
ret=np.copy(pha) |
|
# go through entire list and "iron out" 2pi jumps |
|
for i in range(len(ret)): |
|
# which number to compare to |
|
if i==0: cmpr=clos |
|
else: cmpr=ret[i-1] |
|
# make sure there are no 2pi jumps |
|
ret[i]=no_2pi(ret[i],cmpr) |
|
return ret |
|
|
|
def _array_phases_cont(arr_pha,clos): |
|
"""Reads in 2d array of phases *arr_pha* and makes sure that they |
|
are continuous along first index, i.e., that there are no jumps of |
|
2pi. First array of phasese is made as close to *clos* as |
|
possible.""" |
|
ret=np.zeros_like(arr_pha) |
|
# go over all points |
|
for i in range(arr_pha.shape[0]): |
|
# which phases to compare to |
|
if i==0: cmpr=clos |
|
else: cmpr=ret[i-1,:] |
|
# remember which indices are still available to be matched |
|
avail=range(arr_pha.shape[1]) |
|
# go over all phases in cmpr[:] |
|
for j in range(cmpr.shape[0]): |
|
# minimal distance between pairs |
|
min_dist=1.0E10 |
|
# closest index |
|
best_k=None |
|
# go over each phase in arr_pha[i,:] |
|
for k in avail: |
|
cur_dist=np.abs(np.exp(1.0j*cmpr[j])-np.exp(1.0j*arr_pha[i,k])) |
|
if cur_dist<=min_dist: |
|
min_dist=cur_dist |
|
best_k=k |
|
# remove this index from being possible pair later |
|
avail.pop(avail.index(best_k)) |
|
# store phase in correct place |
|
ret[i,j]=arr_pha[i,best_k] |
|
# make sure there are no 2pi jumps |
|
ret[i,j]=no_2pi(ret[i,j],cmpr[j]) |
|
return ret |
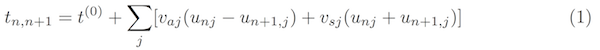
 .
. .
.