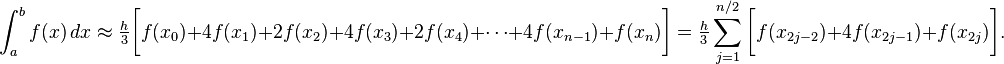andy0130tw/matlab-lab4-lab5.md

## matlab-lab4-lab5.md

      
    Raw
  

              matlab-lab4-lab5.md
            
          
    MATLAB Code


Solution written by Andy Pan
Problems copyrighted by TAs 

Mathematics Software 2015 Spring, NTU
Written with StackEdit, where you can view the full-rendered version.

[TOC]
編者註

以下所有題目皆限定用MATLAB作答，各題除了題目外附上初始的程式碼(boilerplate)以及部分測試(test suite)。各題幾乎都有隱藏的測試點，因此不能盡以附上的測試來驗證程式是否正確。題目敘述盡量按照原規格寫成，並用markdown確保格式一致。數學式方面，原題目皆以圖片排版，其餘的部分本文會用 $\LaTeX$ 排版。
課程網站 ，內含參考解答
Lab 1 Mar.9

1.1 基本介紹

這邊會出現關於問題的敘述，看完後請按右下方「Solve」按鈕即可開始作答。
% 這邊是作答區，請把你的程式貼到這，再按下右下的 Submit，下面的 Test Suite 會把測試資料自動帶入你的程式並列出測試結果。本題不用做任何修改請直接按 Submit 看執行結果。
function c = add( a, b )
    c = a + b;
end

%%
a = 1;
b = 2;
c_correct = 3;
c = add( a, b );
assert( c == c_correct, 'Solution incorrect!' );
1.2 簡單練習

讓我們開始一點簡單的練習吧！這次請修改題目給的 Function Template 使程式輸出為所輸入兩數相乘，也就是使函數 multi 輸入 a, b 輸出為 a*b。
function y = multi(a,b)
    % 將以下的程式碼改為乘法
    y = a+b;
end

%%
a = 1;
b = 5;
c_correct = 5;
c = multi( a, b );
assert( c == c_correct, 'Solution incorrect!' );
%%
a = 2;
b = 3;
c_correct = 6;
c = multi( a, b );
assert( c == c_correct, 'Solution incorrect!' );
%%
a = 4;
b = 6;
c_correct = 24;
c = multi( a, b );
assert( c == c_correct, 'Solution incorrect!' );

1.3 函數呼叫練習

在這個練習中，我們希望你利用 MATLAB 內建的函數找到以下幾個未知數值：

function [ a, b, c, d, e ] = find_values()
    % 將第一小題的答案存在 a，第二小題存在 b，以此類推
end
1.4 矩陣製造練習

在這個練習中，請嘗試創立以下矩陣：

請避免蠻力輸入或是使用迴圈。
function A = create_matrix()
    % A 為題目所列矩陣
end
1.5 解線性系統

在這個練習中，我們希望練習解線性系統。給定三個矩陣 A, B, C，其中 A 為方陣，請求解 A*X = B 與 Y*A = C。
function [ X, Y ] = solve_linear_system( A, B, C )
   % 請求解 A*X = B 與 Y*A = C
end

%%
m = randi( 10 );
n = randi( 10 );
k = randi( 10 );
A = randn( n, n );
X0 = randn( n, k );
Y0 = randn( m, n );
B = A * X0;
C = Y0 * A;
[ X, Y  ] = solve_linear_system( A, B, C );
assert( norm( X - X0 ) < 1e-12, 'Matrix X is incorrect' );
assert( norm( Y - Y0 ) < 1e-12, 'Matrix Y is incorrect' );
1.6 函數的逼近

在這個練習中，我們希望你利用 $N$ 項泰勒展開式來逼近函數 $\log(1+r)$，其中 $N$ 為整數、$-1 < r < 1$。注意項數 $N$ 從第一個非零項開始。
請算出實際值（使用 MATLAB 內建函式）、估計值及絕對誤差。
function [ true, approx, error ] = estimate_log( r, N )
    % true 為實際值、approx 為估計值、error 為誤差。
end
Solutions for selected problems

%%% 1.3 %%%
function [ a, b, c, d, e ] = find_values()
    a = atan(1729);
    b = factorial(17);
    c = factorial(27)/factorial(20)/factorial(7);
    d = gcd(b,c);
    e = max(b,c);
end
%%% 1.4 %%%
function A = create_matrix()
    A=[1:2:100;7:7:350;15:-3:-132;5:6:300];
end
%%% 1.6 %%%
function [ true, approx, error ] = estimate_log( r, N )
    true = log(1+r);
    k = 1:N;
    a = (-1) .^ (k-1) .* r .^ k ./ k;
    approx = sum(a);
    error = abs(true - approx);
end
Lab 3 Mar. 23

3.1 壓縮係數計算

理想氣體，為一種假想的氣體，其性質在 這個頁面 有所介紹。
但很明顯的，現實中的氣體並不是理想氣體，我們使用壓縮係數來測量該現實氣體與理想氣體的差距多大
理想氣體要符合這個 理想氣體方程式

因此，我們定義一個氣體在一個狀態的壓縮係數為

請寫一個函數，在給予氣體壓力、體積、量與溫度下，算出氣體在該狀況下的壓縮係數

壓力的輸入單位是百帕
體積的輸入單位是立方英尺
量的輸入單位是莫爾
溫度的輸入單位是華氏

function Z = compressibility_factor( P, V, n, T )
    % 計算壓縮係數，請注意單位
end

%%
P = rand()*100;
V = rand()*100;
n = rand()*100;
T = rand()*100;
Z0 = reference.compressibility_factor( P, V, n, T );
Z = compressibility_factor( P, V, n, T );
assert( abs( Z-Z0 ) < 1e-3, 'Solution ''Z'' is incorrect!' );
3.1* 除錯練習

% For debugging.
function Z = compressibility_factor( P, V, n, T )
    P = P * 100;
    V = V * 0.028316846592;
    T = ( (T–32) × 5\9 ) + 237.15;
    R = 8.3144621;
    Z = PV / nRT;
end
3.2 統計數據計算

在統計上，一組有 n 筆資料的抽樣資料的的平均數為

而標準差的定義為

另外兩組抽樣資料的共變異的定義為

而相關係數的定義為

請寫一個函數，計算兩組抽樣資料的平均值、標準差與相關係數。以下為函式的輸入與輸出：
格式：
[ meanX, meanY, stdX, stdY, corrXY ] = statistics( X, Y )

輸入：
X, Y:   抽樣資料 (column vectors)

輸出：
meanX:  X 的平均數
meanY:  Y 的平均數
stdX:   X 的標準差
stdY:   Y 的標準差
corrXY: X 與 Y 的相關係數

function [ meanX, meanY, stdX, stdY, corrXY ] = statistics( X, Y )
    % 計算平均值、標準差與相關係數
end

%%
n = 10000;

% Define covariance matrix
sigma1 = randn();
sigma2 = randn();
rho = 1/(1+exp(-randn()));

% Define mean
mu1 = randn();
mu2 = randn();

% Generate random variables
Z1 = randn( n, 1 );
Z2 = randn( n, 1 );
Z3 = rho*Z1 + sqrt(1-rho^2)*Z2;
X = mu1 + sigma1 * Z1;
Y = mu2 + sigma2 * Z3;

% Run Test
[ meanX, meanY, stdX, stdY, corrXY ] = statistics( X, Y );
R = corrcoef( X, Y );
assert( abs( mean(X) - meanX ) < 1e-12, 'The mean of X is incorrect!' );
assert( abs( mean(Y) - meanY ) < 1e-12, 'The mean of Y is incorrect!' );
assert( abs( std(X) - stdX ) < 1e-12, 'The standard deviation of X is incorrect!' );
assert( abs( std(Y) - stdY ) < 1e-12, 'The standard deviation of Y is incorrect!' );
assert( abs( R(1, 2) - corrXY ) < 1e-12, 'The correlation of X and Y is incorrect!' );
3.2* 除錯練習

% For debugging.
function [ meanX, meanY, stdX, stdY, corrXY ] = statistics( X, Y )
    % Get the number of measurements
    n = size(X);
    
    % Compute mean
    meanX = Sum(X) / n;
    meanY = Sum(Y) / n;
    
    % Compute standard deviation
    stdX = Sqrt( Sum( (X-meanX)*(X-meanX) ) ) / n-1;
    stdY = Sqrt( Sum( (Y-meanY)*(Y-meanY) ) ) / n-1;
    
    % Compute covariance
    covXY = Sum( X-meanX * Y-meanY ) / n-1;
    
    % Compute correlation
    corrXY = covXY / stdX*stdY;
end
3.3 線性系統更新

考慮以下的線性系統：

其中 y 與 beta 是 column vector， X 是 matrix。假設 X 為 full-rank 且 row 比 column 多，則這個線性系統的 least square solution 會是

在這個練習中，我們考慮一個特殊的情況，於已知 X, y, beta_hat 的情況下，在 X 的最後增加一個 column，則我們可以在不用重新計算反矩陣的情況下，利用以下公式計算新的線性系統的 least square solution：

其中 $A$ 為 symmetric matrix，$b$ 為 column vector，$c$ 為 scalar，$k = c - b' \times inv(A) \times b$。
請寫一個函數，計算線性系統增加一個新的 column之後的 least square solution。以下為函式的輸入與輸出：
格式：  `[ invA, beta ] = linear_system_update( X, x_new, y, invA, beta )`

輸入： 
X:     原先的 $X$
x_new: $X$ 的新 column
y:     y
invA:  $X' \times X$ 的反矩陣 
beta:  原先的 least square solution

輸出：
invA:  更新後的 $X' \times X$ 的反矩陣 
beta:  更新後的 least square solution

3.3* 除錯練習

% For debugging.
function [invA, beta] = linear_system_update( X, x_new, y, invA, beta )
    [k, ~] = size( X );
    b = X' * x_new;
    d = invA * b;
    k = 1 / (x_new' * x_new - b' * d);
    d = [d; -1];
    invA = [invA, zeros(k, 1)];
    invA = [invA; zeros(1, k)];
    invA = invA + k * (d * d');
    theta = X' * y;
    beta = beta + k * d' * theta * d;
end
Solutions

%%% 3.1 %%%
function Z = compressibility_factor( P, V, n, T )
    % Output the compressibility factor given by its P, V, n, and T.
    % Andy Pan, 2015/3/23

    % Variables:
    %  P input   Pressure in hPa
    %  V input   Volume   in cubic foot
    %  n input   quantity in mole
    %  T input   temp.    in degF
    %  Z output  compressibility factor = PV/nRT.

    % convert P: hPa -> atm
    P = P / 1013.25
    % convert V: cbft -> L
    V = V * (2.54 * 12)^3 / 1e3
    % convert T: degF -> Kelvin
    T = (T-32)*5/9 + 273.15
    %Compute Z, assume proper unit
    Z = P * V/ (n * 0.08205746 * T)
end
%%% 3.2 %%%
function [ meanX, meanY, stdX, stdY, corrXY ] = statistics( X, Y )
    % Caculate mean value, std. deviation, and correlation coeff. given X, Y.
    % Variables: 
    %  X, Y          inputs:  two vectors of data
    %  meanX, meanY  outputs: mean values of X and Y.
    %  stdX , stdY   outputs: standard deviation of X and Y.
    %  corrXY        output:  correlation coefficient of X-Y.
    %  len           local:   vector dimension.
    %  covar         local:   co-variation between X-Y.
    %  sumX , sumY   local:   sum of X and Y.
    %  sumX2, sumY2  local:   sum of X^2 and Y^2.

    len    = length(X);
    sumX   = sum(X);
    sumY   = sum(Y);
    sumX2  = sum(X .^ 2);
    sumY2  = sum(Y .^ 2);
    meanX  = sumX / len;
    meanY  = sumY / len;
    stdX   = sqrt((sumX2 - meanX ^ 2 * len) / (len-1));
    stdY   = sqrt((sumY2 - meanY ^ 2 * len) / (len-1));
    covar  = (sum(X .* Y) - meanX * meanY * len) / (len-1);
    corrXY = covar / stdX / stdY;

end
%%% 3.2* %%%
% hint: you can use diff to view what was changed
function [ meanX, meanY, stdX, stdY, corrXY ] = statistics( X, Y )
    % Get the number of measurements
    n = length(X);
    
    % Compute mean
    meanX = sum(X) / n;
    meanY = sum(Y) / n;
    
    % Compute standard deviation
    stdX = sqrt( sum( (X-meanX).*(X-meanX) )  / (n-1));
    stdY = sqrt( sum( (Y-meanY).*(Y-meanY) )  / (n-1));
    
    % Compute covariance
    covXY = sum( (X-meanX) .* (Y-meanY))  / (n-1);
    
    % Compute correlation
    corrXY = covXY / stdX/stdY;
end
%%% 3.3 %%%
function [invA, beta] = linear_system_update( X, x_new, y, invA, beta )
    % Update linear system y = X * beta without re-computing invA.
    % Andy Pan, 2015/3/23

    % Variables:
    %  X     input:  initial X
    %  x_new input:  new X
    %  y     input:  vector y
    %  invA  input:  initial A inverse
    %  beta  input:  initial beta
    %  invA  output: updated A inverse
    %  beta  output: updated beta
    %  mat?? local:  block matrix of the new invA
    b = X' * x_new;
    c = sum(b .^ 2);
    k = c - b' * invA * b;
  
    matTL = invA + invA * b * b' * invA / k;
    matTR = invA * b / (-k);
    matBL = b' * invA / (-k);
    matBR = 1 / k;

    invA = [matTL, matTR; matBL, matBR];    
    beta = invA * [X,x_new]' * y;
end
%%% 3.3* %%%
% hint: you can use diff to view what was changed
function [invA, beta] = linear_system_update( X, x_new, y, invA, beta )
    [ ~, m] = size( X );
    b = X' * x_new;
    d = invA * b;
    k = 1 / (x_new' * x_new - b' * d);
    d = [d; -1];
    invA = [invA, zeros(m, 1)];
    invA = [invA; zeros(1, m+1)];
    invA = invA + k * (d * d');
    X = [X,x_new];
    theta = X' * y;
    beta = [beta;0] + k * (d' * theta) * d;
end
Lab 4 Mar. 30

4.1 牛頓法

牛頓法 是一種利用迭代求方程式解的辦法 迭代的公式是

迭代結束的條件是函數值足夠靠近0，或著是達到最高的迭代次數


f: 輸入的函數，f(x) 會回傳 f在x的值


d_f: 輸入的函數，為f的微分，d_f(x)會回傳d_f在x的值


x_0 : 輸入，迭代的起始值


n :輸入，最大迭代次數


tol : 輸入，函數值離0多近視為結束


x : 輸出，收斂到的x值


% test suites:
% #1: f=@(x)2*x-7; d_f=@(x)2; x_0=0;
% #2: f=@(x)sin(x); d_f=@(x)cos(x); x_0=0;
% #3: f=@(x)x.^2-4; d_f=@(x)2*x; x_0=0.1;
%%
n=1000;
tol=1e-12;
x_ref=reference.your_newton(f,d_f,x_0,n,tol);
x_you=your_newton(f,d_f,x_0,n,tol);
assert(abs(x_you-x_ref)<2*tol);
4.2 影像模糊化


影像模糊，其基本概念是將一個像素與其周圍的像素取平均。 平均的算法有很多種，商業軟體所用的方法是使用高斯模糊
這邊，我們用的是比較簡單的算法，就是將自己與周圍附近像素去做算術平均

上圖的算式就是跟自己周圍距離1的像素做平均
現在我們輸入一個矩陣A，請將A利用上述算式進行模糊化
在邊緣角落的部分，就與邊界內所有鄰近格子平均
有興趣的人可以試著寫與鄰近n格平均的版本 (鄰近兩格: 周圍共25格平均, 鄰近3格: 總共49格平均)
關於matlab如何讀取圖片的部分，可以參考這篇文件
裡面有提到怎麼讀影像檔，跟把讀進來的矩陣轉成RGB格式的方法
% test suites:
% #1: m=100; n=50;
% #2: m=50; n=100;
% #3: m=120; n=80;
% #4: m=400; n=200;
% #5: m=800; n=40;
%%
A=rand(m,n);
ans_A=reference.mat_blur(A);
your_A=mat_blur(A);
assert(norm(ans_A-your_A)<1e-12,'The blurring is incorrect.')
Solutions

Lab 4.1 - Simple Newton Method

function x = your_newton(f, d_f, x_0, n, tol)
  x = x_0;
  k = 0;
  while abs(f(x) > tol) & k < n
    % iteration
    x = x - f(x) / d_f(x);
    k = k+1;
  end
end
Lab 4.2 - Matrix Blurring

function newA = mat_blur(A)
  % A:    input matrix
  % newA: output blurred matrix
  [m, n] = size(A);
  % need a matrix of the same size
  B = A;
  for i = 1:m
    for j = 1:n
      B(i, j) = cal_blur(A, i, j, m, n);
    end
  end
  newA = B;
end

function avg = cal_blur(A, x, y, m, n)
  % Calculate the average value of an element
  %  and its surrounding ones
  sur = 0;
  avg = 0;
  for i = -1:1
    for j = -1:1
      nx = x + i;
      ny = y + j;
      if 0 < nx && nx <= m && 0 < ny && ny <= n
        sur = sur + 1;
        avg = avg + A(nx, ny);
      end
    end
  end
  avg = avg / sur;
end
Lab 5 Apr. 6


This lab is about GCD (最大公因數).
Test suites are identical for this lab (as shown below).
Boilerplate is omitted.


% test suites:
% #12: a = randi(65536); b = randi(65536);
% #34: a = randi(65536); b = randi(65536);
%       l = gcd( a, b ); a = a / l; b = b / l;
% #5~8: l = randi(4096);
%       a = randi(4096) * l;
%       b = randi(4096) * l;
%%
tic;
d = gcd_by_filter( a, b );
toc;
assert( d == gcd( a, b ), 'The answer is incorrect!' );


5.1 Reverse Search Algorithm

兩個正整數 a 與 b 的最大公因數 gcd(a, b) 定義為能夠同時整除 a 與 b 的正整數當中最大的那一個。計算最大公因數的方法有很多種，首先我們要先嘗試最簡單的方法：Reverse Search Algorithm。
Reverse Search Algorithm 的想法如下：

從 a 與 b 中較小的數字開始，逐次減少 1 直到找到一個數字可以同時整除 a 與 b。

請寫個函式，利用 Reverse Search Algorithm 計算 a 與 b 的最大公因數。
5.2 Filtering Algorithm

大家可以很輕易的發現，Reverse Search Algorithm 是個很沒有效率的方法，尤其是當 a 與 b 很大的時候更為明顯。
接著我們要嘗試 Filtering Algorithm ，這個方法的原理是基於這個等式： $$gcd(a, b) = k \times \gcd \left(\frac{a}{k}, \frac{b}{k} \right)$$。身為數學系的學生，想必可以輕易證明這條等式。
Filtering Algorithm 的想法如下：

令 $d$ 為 $1$

從 $k=2$ 開始，逐次增加 $1$ 直到 $k$ 為 $a$ 與 $b$ 的共同因數為止。
將 $d$ 乘上 $k$，$a$ 除以 $k$，$b$ 除以 $k$。
重複步驟 2–3 直到找不到共同因數為止，這時的 $d$ 就是最大公因數。

請寫個函式，利用 Filtering Algorithm 計算 a 與 b 的最大公因數。
5.3 Faster Filtering Algorithm

接下來我們要加速 Filtering Algorithm。Filtering Algorithm 的步驟 2 總是從 2 開始尋找公因數，但是這樣的找法相當沒有效率。假設在步驟 3 的時候已經找到 5 為的公因數，那這時的 $a$ 與 $b$ 顯然沒有比 5 還小且大於 1 的非負公因數了。因此我們 Filtering Algorithm 修改成以下的樣子：

令 $d$ 為 $1$， $s$ 為 $2$

從 $k=s$ 開始，逐次增加 1 直到 $k$ 為 $a$ 與 $b$ 的共同因數為止。
將 $d$ 乘上 $k$，$a$ 除以 $k$，$b$ 除以 $k$，並令 $s$ 為 $k$。
重複步驟 2–3 直到找不到共同因數為止。

請寫個函式，利用 Faster Filtering Algorithm 計算 a 與 b 的最大公因數。
5.4 Euclidean Algorithm

到目前為止的演算法都還是用一個一個嘗試的方式來找公因數，但這樣的方法相當沒有效率，我們不應該就此滿足。現在我們要介紹最古早的演算法之一：Euclidean Algorithm，又稱為輾轉相除法，這個演算法最早可以追逤到公元前 300 年的歐幾里德《幾何原本》。MATLAB 內建的最大公因數函式就是使用這個演算法。
Euclidean Algorithm 的想法如下：

令 $m = \max(a, b)$ ， $n = \min(a, b)$。
求 $m$ 除以 $n$ 的餘數 $r$，然後令 $m = n$ ， $n = r$ 。
重複步驟 3 直到整除為止，這時的 $n$ 就是最大公因數。

請寫個函式，利用 Euclidean Algorithm 計算 a 與 b 的最大公因數。
5.5 Binary Algorithm

最後，我們要介紹一個特殊的演算法：Binary Algorithm，這個演算法的特點在於他只需要乘二、除二與減法而已，由於在電腦計算上，乘二跟除二特別有效率，因此這個演算法在電腦計算上特別快，但由於演算法較為複雜且所需的迴圈次數較多，Euclidean Algorithm 仍然是最常用的演算法。
Binary Algorithm 的想法如下：

令 $m = \max(a, b)$ ， $n = \min(a, b)$ ， $d = 1$ 。
若 $m$ 與 $n$ 都是偶數，則同時除以二，並使 $d$ 乘二；若只有一個是偶數，則只有那個數字除以二（d 不用改變）。
這時若 $n$ 比 $m$ 大，交換兩數。接著令 $m$ 為 $m-n$。
重複步驟 2–3 直到 $m$ 歸零，這時的 $d\times n$ 就是最大公因數。

請寫個函式，利用Binary Algorithm 計算 a 與 b 的最大公因數。
Solutions

Lab 5.1 GCD by Enumeration

function d = gcd_by_reverse_search( a, b )
  x = min(a, b);
  d = 1;
  while x > 1
    if mod(a, x) == 0 & mod(b,x ) == 0
      d = x;
      return;
    end
    x = x-1;
  end
end
Lab 5.2~3 - GCD by Filtering

function d = gcd_by_filter( a, b )
  % Calculate gcd by simple filtering
  d = 1;
  m = min(a, b);
  k = 2;
  % Since gcd(a,b)<min(a, b)
  while k < m
    if mod(a, k) == 0 & mod(b, k) == 0
      d = d*k;
      a = a/k;
      b = b/k;
      m = min(a, b);
      k = 2;  % for Lab 5.3, delete this line
    else
      k = k+1;
    end
  end
end
Lab 5.4 - GCD Euclidean Algorithm

% This code uses recursion.
% My favorite version!
% Keep in mind that the recursion is not always
%  helpful unless it won't cause stack overflow!
function d = gcd_by_euclid( a, b )
    if a > b;      d = gcd_by_euclid(b, a);
    elseif a == 0; d = b;
    else           d = gcd_by_euclid(mod(b, a), a);
    end
end
Lab 5.5 - GCD Binary Optimization

% I don't really understand what this means.
function d = gcd_by_binary( a, b )
  if a > b
    d = gcd_by_binary(b, a);
    return;
  end
  d = 1;
  while b > 0
    aa = ~mod(a, 2);
    bb = ~mod(b, 2);
    if aa; a = a / 2; end;
    if bb; b = b / 2; end;
    if aa && bb; d = d * 2; end;
    
    if a > b
      p = b;
      b = a;
      a = p;
      
    end
    b = b - a;
  end
  d = d * a;
end
Midterm Apr. 20


考試時間 4/20 PM3:30~6:45
開放查詢任何資料，但不允許交談及使用通訊軟體。
每題佔分 15 分，共 120 分；滿分為 100 分，其餘 20 分為額外加分。
每題皆有多個測資，分數將取決於測資通過數量。
考試結束後助教會重新測試全部題目的程式，並且以最後上傳的 code 為考試分數依據。

p1


Problem Summary:
TEMPLATE:  [k, f_seven] = problem_one() 
INPUT:
(none)
OUTPUT: 
k : the constant  f_seven: number of milligram left
    after 7 days

p2


Problem summary:
TEMPLATE:
K = problem_two()

INPUT:
(none)

OUTPUT:
K: discharge factors of x in the range 0.45 to 0.90 in steps of 0.05

p3

Mean is an ambiguous word. There's many different way to calculate mean for a data set. And they can have drastically different result.
In this question we give you an row vector x, and you're required to calculate:


Its arithmetic mean


Its geometric mean


Its harmonic mean


Its median (If n odd, it's the number in the center, if n even, it's the arithmetic mean of center two numbers)


Its mid-range


After calculating these, also calculate the largest difference between the above methods.

Problem summary:
Template
[means, max_diff] = problem_three( x )

INPUT:
x:        a row vector containing the data set to be calculated

OUTPUT:
means:    a row vector with length 5:
means(1): Arithmetic mean of x
means(2): Geometric mean of x
means(3): Harmonic mean of x
means(4): Median of x
means(5): Mid-Range of x
max_diff: the maximum difference in absolute value between two entries of the 'means' vector

% test suites:
% #1: n = 30;
% #2: n = 80;
%%
x = rand(1, n);
[means0, max_diff0] = reference.problem_three(x);
[means, max_diff] = problem_three(x);
assert(abs(means(1)/means0(1) - 1) < 1e-12, 'Arithmetic mean incorrect!');
assert(abs(means(2)/means0(2) - 1) < 1e-12, 'Geometric mean incorrect!');
assert(abs(means(3)/means0(3) - 1) < 1e-12, 'Harmonic mean incorrect!');
assert(abs(means(4)/means0(4) - 1) < 1e-12, 'Median incorrect!');
assert(abs(means(5)/means0(5) - 1) < 1e-12, 'Mid-range incorrect!');
assert(abs(max_diff/max_diff0 - 1) < 1e-12, 'Maximum difference incorrect!');
p4

級數收斂通常寫為

級數收斂一項重要的指標是級數收斂的速度，也就是要幾項這級數會與收斂的目標夠近，也就是 相對誤差 足夠小

以下是函式格式：

格式：
n = problem_four( f, S, tol )


輸入：
f: 一個函數，輸入 n 時會回傳 f(n)，數列第 n 項的值
S: 級數最後收斂的值
tol: 當 n 項級數和與 S 的相對誤差的絕對值小於此值時即視為數值收斂


輸出：
n: 數值收斂所需要的項數

 	
% test suites:
% #1: f = @(x) rand_factor ./ (x.^2);
%     S = rand_factor * pi^2 / 6;
%     tol = 1e-4;
% #2: f = @(x) rand_factor ./ (2.^x);
%     S = rand_factor;
%     tol = 1e-8;
%%
rand_factor = randn;
%%% insert conditions here
n = problem_four(f, S, tol);
n0 = reference.problem_four(f, S, tol);
assert(abs(n/n0 - 1) < .01, 'Answer incorrect!');
p5

在數值分析上，有許多方法可以計算定積分。假設要求函數 f(x) 在區間 [a, b] 的積分，常用的方法是切割區間來估計。
最基礎的方法是用 黎曼和 (Riemann sum)，方法是對將 [a, b] 切割成 n 等份，以區間的左端／中點／右端的函數值作為高畫矩形，然後加總矩形的面積作為估計。

若使用梯形取代矩形，這種方法稱為 梯形法 (Trapezoid rule)

在這邊要介紹的是 辛普森法 (Simpson's rule)，這個方法使用二次曲線來估計。

令h = (b-a)/n，x_j = a + jh，辛普森法的公式可以寫成

另外也可以使用四次曲線來估計 ( Simpson's 3/8 rule )，這樣的公式則會是


請寫一個函式，計算函數 f(x) 在區間 [a, b] 用 Simpson's 3/8 rule（四次曲線逼近）估計的積分。以下為函式格式：

格式：
value = problem_five( f, a, b, n )


輸入：
f: 函數， f(x) 為 f 在 x 的值，輸入 x 可為向量（此時的輸出為 componentwise 的函數值）
a: 區間左端點
b: 區間右端點
n: 分割子區間數，必定為 3 的倍數


輸出：
value: 估計的積分值

% test suites:
% #1: f = @(x) rand_factor * x.^2;
%     a = 2; b = 4; n = 6;
% #2: f = @(x) rand_factor * sin(x);
%     a = 0; b = pi; n = 18;
%%
rand_factor = randn;
%%% insert conditions here
value0 = reference.problem_five(f, a, b, n);
value = problem_five(f, a, b, n);
assert(abs(value/value0 - 1) < 1e-8, 'The value is incorrect!');
p6

數學系的課堂當率如下（每年都恰好有這樣比例的人被當，無條件捨去至整數位）：

大一上有微積分甲上，當率 21.4%；大一下有微積分甲下，當率 13.6%
大二上有分析導論上，當率 11.2%；大二下有分析導論下，當率 28.9%

假設要修過微積分甲上才能修微積分甲下，要修過微積分甲下才能修分析導論上，要修過分析導論上才能修分析導論下，若課程被當只能明年重修（上下學期開的課程不相同）。每個人每學期一定會修目前可以修的課。
今年為數學系的第一屆，每年都恰好有 k 個新生加入微積分甲上的課堂。若沒有修業年限的限制，請計算第 n 屆學生入學那一年的下學期，分析導論下的課堂上有多少學生。

以下為函式格式：

格式：  number = problem_six( n, k )


輸入：
n: 第 n 年
k: 每年新生數


輸出：
number: 第 n 年分析導論下的修課學生數

%%
n = 1;
k = 60;
number0 = reference.problem_six(n, k);
number = problem_six(n, k);
assert( number0 == number, 'The value is incorrect' );
p7

在 Lab 4 的時候，我們進行了 很陽春的影像模糊化，這裡我們要進行比較複雜的 高斯模糊 。
模糊化要進行兩個步驟：
首先計算出 blurring kernal，這是一個矩陣，表示該像素附近的像素在模糊化後所佔的比例，像素本身通常在矩陣中央

接著對每一個像素，使用上面產生的矩陣為係數進行加權平均

在第一步中，我們需要把 高斯函數 進行離散化，剛好 MATLAB 有提供這樣的 函數 來幫我們進行這個工作。使用方法可以參考 這個網頁。
第二步就跟我們在 Lab 4 做的很像，只不過這次權數不全為 1，在邊緣的情況就是只有在邊界內的像素要被平均。

以下為函式格式：

格式：
A_blur = problem_seven( A, n, sigma )


輸入：
A: 要進行高斯模糊的矩陣
n: 每個像素要跟周圍幾個像素進行加權平均（周圍兩格：總共共 25 格平均，周圍 3 格：總共 49 格平均）
sigma: 計算高斯模糊的參數


輸出：
A_blur: 高斯模糊後的矩陣


步驟：

使用 n 跟 sigma 計算出權數矩陣
使用權數矩陣來對 A 進行高斯模糊

% test suites:
% #1: n = 1; sigma = 1;
% #2: n = 3; sigma = 0.5;
%%
A = rand(20, 20);
A_blur0 = reference.problem_seven(A, n, sigma);
A_blur = problem_seven(A, n, sigma);
assert(norm(A_blur-A_blur0) < 1e-12, 'Answer incorrect!');
p8 (bonus)

梭哈（Show Hand，正式名稱是 Five-card stud）是常見的撲克牌遊戲之一。這個遊戲的目的是做成最大的牌型並贏得賭局，每種牌型皆是五張撲克牌的組合。撲克牌的牌面數字大小依序為 A > K > Q > J > 10 > 9 > … > 3 > 2；牌型大小依序為：皇家同花順＞同花順＞四條＞葫蘆＞同花＞順子＞三條＞兩對＞一對＞高牌。 為了簡化題目，牌型大小不比較花色。
牌型的詳細介紹如下：

皇家同花順（Royal Straight Flush）： 同花色的 A、K、Q、J、10。若雙方都是皇家同花順，則平手。 例：A♠ K♠ Q♠ J♠ 10♠
同花順（Straight Flush）： 五張同花色的連續牌，但不接受 2 與 K 同時出現的牌型。若雙方皆是同花順，由數字最大的牌決定牌型大小，若相同則比較次大的牌。如果數字全部相同則平手。特別注意 A K Q J 10 > 5 4 3 2 A > K Q J 10 9。 例：Q♦ J♦ 10♦ 9♦ 8♦
四條（Four of a kind）： 由四張相同點數及一張不同的撲克牌組成。若雙方皆是四條，由四張相同點數牌的數字決定牌型大小。 例：4♣ 4♦ 4♥ 4♠ 9♥
葫蘆（Full house）： 由三張相同點數及兩張其他相同點數的撲克牌組成。若雙方皆是葫蘆，由三張相同點數牌的數字決定牌型大小。 例：8♣ 8♦ 8♠ K♥ K♠
同花（Flush）： 由五張不按順序但相同花色的撲克牌組成。若雙方皆是同花，由數字最大的牌決定牌型大小，若最大的牌相同，則比較第二、第三、第四或者第五張牌。若全部相同則平手。 例：K♠ J♠ 8♠ 4♠ 3♠
順子（Straight）： 由五張連續牌組成，但不接受 2 與 K 同時出現的牌型。若雙方皆是順子，則由數字最大的牌決定牌型大小，若相同則比較次大的牌。如果數字全部相同則平手。特別注意 A K Q J 10 > 5 4 3 2 A > K Q J 10 9。 例：5♦ 4♥ 3♠ 2♦ A♦
三條（Three of a kind）： 由三張相同點數和兩張不同點數的撲克牌組成。若雙方皆是三條，由三張相同點數牌的數字決定牌型大小。 例：7♣ 7♥ 7♠ K♦ 2♠
兩對（Two pair）： 由兩對數字相同但兩兩不同的撲克牌和隨意的一張牌組成。若雙方皆是兩對，由數字較大的對子決定牌型大小，若相同則比較另一個對子，若果對子數字都相同，則由第五張牌來決定牌型大小。如果數字全部相同則平手。 例：A♣ A♦ 8♥ 8♠ Q♠
一對（One pair）： 由兩張相同點數的撲克牌和另三張無法組成牌型的牌組成。若雙方皆是一對，由對子決定牌型大小，若相同則依序比較剩下的三張牌。如果數字全部相同則平手。 例：9♥ 9♠ A♣ J♠ 4♥
高牌（High card）： 無法組成以上任一牌型的散牌。若雙方都是高牌，由數字最大的牌決定牌型大小，若最大的牌相同，則比較第二、第三、第四或者第五張牌。若全部相同則平手。 例：A♦ 10♦ 9♠ 5♣ 4♣


請寫一個函式，判斷兩個牌型的大小關係。特別注意兩個牌型皆從同一副牌中取出，也就是說不會有重複的牌出現。在函式中，用下列代號代表各個撲克牌：

1=A♠, 2=2♠, 3=3♠, …, 10=10♠, 11=J♠, 12=Q♠, 13=K♠,
14=A♥, 15=2♥, 16=3♥, …, 23=10♥, 24=J♥, 25=Q♥, 26=K♥,
27=A♦, 28=2♦, 29=3♦, …, 36=10♦, 37=J♦, 38=Q♦, 39=K♦,
40=A♣, 41=2♣, 42=3♣, …, 49=10♣, 50=J♣, 51=Q♣, 52=K♣

以下為函式格式：

格式：
win = problem_eight( hand1, hand2 )


輸入：
hand1: 玩家一的牌，為 1×5 的 row array
hand2: 玩家二的牌，為 1×5 的 row array


輸出：
win: 若玩家一的牌比較大，則輸出 1；若玩家二的牌比較大，則輸出 2；若平手，則輸出 0


提示：

把代表撲克牌的代號轉換成花色跟數字，並且用 14 代表 A 來處理大小關係。
判斷花色是否相同。
將數字按照大小排序。
計算每個玩家的牌有幾個重複的數字。

% test suites: (modified for easier stating)
% #1: hand1 = [15 18 16 19 17];
%     hand2 = [49 14 40  1 27]; win_0 = 1;
% #2: hand1 = [37 13 40 25 49];
%     hand2 = [27 30 38 32 29]; win_0 = 2;
% #3: hand1 = [17 30 10 36 52];
%     hand2 = [14 12 27 15 16]; win_0 = 1;
% #4: hand1 = [26 27 28 29 30];
%     hand2 = [12 13 14 15 16]; win_0 = 2;
% #5: hand1 = [28 22 17 48 29];
%     hand2 = [45 43  8  9 49]; win_0 = 1;
%%
win = problem_eight(hand1, hand2);
assert((win==win_0), 'Answer incorrect!');
Solutions for selected problems

%%% p3 %%%
function [means, max_diff] = problem_three( x )

n = length(x);
means = zeros(1, 5);

means(1) = sum(x) / n;
means(2) = prod(x) ^ (1 / n);
means(3) = (sum(1 ./ x) / n) ^ (-1);
means(4) = median(x);
means(5) = (max(x) + min(x)) / 2; 

max_diff = max(means) - min(means);

end
%%% p4 %%% note that there is a test point is actually invalid
function n = problem_four(f,S,tol)
  w = f(1);
  n = 1;
  while abs(w / S - 1) >= tol
    n = n + 1;
    w = w + f(n);
  end
end
%%% p5 %%%
function value = problem_five( f, a, b, n )

h = (b - a) / n;
mul = [1, 3, 3,repmat([2, 3, 3], 1, n / 3 - 1), 1];
interp = linspace(a, b, n + 1);
val = f(interp);

value = (3 / 8) * h * sum(mul .* val);

end
%%% p6 %%%
function number = problem_six( n, k )

  p1 = .214;
  p2 = .136;
  p3 = .112;
  p4 = .289;

  v = zeros(8, 1);

  for i = 1:n
    v(1) = v(1) + k;
    vo = zeros(8, 1);
    vo(1) = 0;
    vo(2) = pa(v(1), p1) + v(2) + v(6);
    vo(3) = 0;
    vo(4) = pa(v(3), p3) + v(4) + v(8);
    vo(5) = fa(v(1), p1) + v(5);
    vo(6) = 0;
    vo(7) = fa(v(3), p3) + v(7);
    vo(8) = 0;
    
    v = vo;

    if i ~= n
      vo(1) = v(1) + v(5);
      vo(2) = 0;
      vo(3) = pa(v(2), p2) + v(3) + v(7);
      vo(4) = 0;
      vo(5) = 0;
      vo(6) = fa(v(2), p2) + v(6);
      vo(7) = 0;
      vo(8) = fa(v(4), p4) + v(8);
    end

    v = vo;
  end

  number = v(4);

end


function a = fa(n, percent)
  a = floor(n * percent);
end

function b = pa(n, percent)
  b = n - fa(n, percent);
end
%%% p7 %%%: sorry for that
%%% p8 %%%: sorry for that
Lab 7 May. 15

7.1 Vigenère Cipher

維吉尼亞密碼 （Vigenère Cipher）是使用一系列凱撒密碼組成密碼字母表的加密算法，屬於多表密碼的一種簡單形式。
讓我們透過以下的舉例說明維吉尼亞密碼。假設明文為：
ATTACKATDAWN

選擇某一關鍵詞並重複而得到密鑰，如關鍵詞為 LEMON 時，密鑰為：
LEMONLEMONLE

對於明文的第一個字母 A，對應密鑰的第一個字母 L，L 在英文字母中是第 12 個字母，故將 A 向後推移 (12-1) = 11 個字母，得到密文第一個字母 L。
明文第二個字母為 T，使用密鑰的第二個字母 E 進行加密，向後推移 4 個字母，得到密文第二個字母 X。
明文第三個字母為 T，使用密鑰的第三個字母 M 進行加密，向後推移 12 個字母，推得密文的第三個字母應該是英文字母的第 32 個字母。由於英文字母只有 26 個，所以要折回到 A 繼續數，得到密文的第三個字母為第六個英文字母 F。
以此類推，可以得到：
明文：ATTACKATDAWN
密鑰：LEMONLEMONLE
密文：LXFOPVEFRNHR

解密的過程則與加密相反，改為向前推移。
在數學上的操作可以以 $025$ 代表字母 AZ，以 $P_i$ 表示第 $i$ 個明文字母、 $K_i$ 表示第 $i$ 個密鑰字母、 $C_i$ 表示第 $i$ 個密文字母，則維吉尼亞密碼的加密方法可以寫成同餘的形式：
$$C_i ≡ P_i + K_i;;(\bmod 26)$$
解密方法也可以寫成同餘的形式：
$$ P_i ≡ C_i - K_i;;(\bmod 26)$$

請寫一個函式，給予密文與密鑰的關鍵字，解密出對應的明文。函式格式如下：
格式：
plaintext = vigenere_decipher( ciphertext, keyword )

輸入：
ciphertext: 密文，皆為大寫
keyword:    關鍵字，皆為大寫

輸出：
plaintext:  明文，皆為大寫


提示：


注意題目為解密而非加密。


可用 c-'A' 求出字元 c 代表的數字。例：若 c='K' ，則 c-'A' 等於 10。參考： ASCII 。


可用 char(n+'A') 求出數字 n 對應的字母。例：若 n=10 ，則 char(n+'A') 為字母 K。


可使用 加密程式 來測試。加密程式的格式如下：
格式：
ciphertext = vigenere_encipher( plaintext, keyword )

輸入：
plaintext:  明文，皆為大寫
keyword:    關鍵字，皆為大寫

輸出：
ciphertext: 密文，皆為大寫


%%
plaintext = 'ATTACKATDAWN';
ciphertext = 'LXFOPVEFRNHR';
keyword = 'LEMON';
plaintext_student = vigenere_decipher( ciphertext, keyword );
assert( isequal( plaintext, plaintext_student ), 'The plaintext is incorrect!' );
7.2 Inverse Distance Weighting Interpolation

插值法，是利用已知值的點來估計任意點的值的辦法。
插值有很多種方法，有線性逼近，拋物線逼近等，這些方法使用目標附近的點來逼近
在這邊要介紹的這種插值，是用 所有 已知的點進行加權平均來估計，每個點的權重是他與目標點距離倒數的某個次方。
也就是說，如果已知點是

而目標點是 $\mathbf{x} $ 的話，則各點權重就是

其中 $p$ 是給定的參數
而內插結果就是

注意到，如果目標點是已知點，那結果很明顯就是已知該點的值
本題使用的距離是歐式距離，也就是 各分量平方和開根號
計算範例: 本題第一個測資：

target_x=2.5 因此目標與已知點的距離分別是 $1.5, 0.5, 0.5, 1.5$
在 p=2 的情況下，權重就是

所以內插的結果就是


INPUT:

Known_x : 一個 mxn 的矩陣，記載 m 個已知點在 n 維空間的座標
Known_value : 一個 mx1 的向量，記載在 Known_x 點上的值： Known_x(i,:) 上的值為Known_value(i)
target_x : 一個 1xn 的向量，為目標點的座標
p: 一個大於 0 的數，為計算的參數

OUTPUT:

int_value : 利用此方法內插估計的值

%%
Known_x=[1;2;3;4];
Known_value=[4;3;1;6];
target_x=2.5;
p=2;
goal=2.3;
your_ans=your_interpolation(Known_x,Known_value,target_x,p);
assert((goal-your_ans)/goal<1e-10,'Wrong answer on 1st test');
%%
Known_x=(-5:1:9)';
Known_value=Known_x.^2;
target_x=3;
p=2;
goal=9; your_ans=your_interpolation(Known_x,Known_value,target_x,p); 
assert((goal-your_ans)/goal<1e-10,'Wrong answer on 2nd test');
Solutions

%%% 7.1 %%%
function plaintext = vigenere_decipher( ciphertext, keyword )

clen = length(ciphertext);
klen = length(keyword);

k = zeros(1, clen);

for i = 1:clen
  k(i) = keyword(mod(i - 1, klen) + 1) - 'A';
end

plaintext = mod(ciphertext - 'A' - k, 26) + 'A';

end
%%% 7.2 %%%
function int_value = your_interpolation(Known_x,Known_value,target_x ,p)

  [m, n] = size(Known_x);
  tx = repmat(target_x, m, 1);
  
  d = arrayfun(@(x) norm(Known_x(x, :) - target_x), 1:m) .^ (-p);
  for j = 1:m
    if d(j) == inf
      int_value = Known_value(j);
      return;
    end    
  end
  dw = d * Known_value;
  int_value = sum(dw) / sum(d);
end
Final


考試時間 6/22 PM3:45~6:15


開放查詢任何資料，但不允許交談及使用通訊軟體。


每題皆有多個測資，分數將取決於測資通過數量，有複數函數輸出的題目有部分給分。


考試結束後助教會重新測試全部題目的程式，並且以最後上傳的 code 為考試分數依據。


預計6/24上午公布期末考成績。


對期末考成績有疑慮的，6/25下午13:00~15:00可以來天文數學館439室找助教討論。


該時段不能過來的，可以使用信件或facebook與助教聯繫討論。


請於6/23早上06:00前，將你們這組的「期末報告(PDF)」、「程式碼(ZIP)」上傳至 這個資料夾。


p1. Conjugate Gradient

共軛梯度法，是求解對稱正定線性方程組的數值解的方法。共軛梯度法是一個疊代方法，它適用於稀疏矩陣線性方程組，因為這些系統對於像 Cholesky 分解這樣的直接方法太大了。這種方程組在數值求解偏微分方程時很常見。
讓我們跳過冗長的敘述，直接看這個演算法的敘述（可直接參考 維基的內容）：
我們要解 $A\mathbf{x}=\mathbf{b}$ 這個線性系統，其中 $A$ 對稱（$A = A'$）且正定 ($\mathbf{x}'A\mathbf{x} &gt; 0$ 對於所有非零的 $\mathbf{x}$)。


首先，令 $x_0 = 0$ 、 $k = 0$ 、 $\mathbf{r}_0 = \mathbf{b}$


執行以下動作（3~8）直到 $\mathbf{r}_k$ 夠小（$\mathrm{norm}(\mathbf{r_k})$ 小於給定的數字）


$k = k + 1$


若 $k = 1$， $\mathbf{p}_1 = \mathbf{r}_0$


若 $k &gt; 1$，$$\mathbf{p}k = \mathbf{r}{k-1} + \frac{\mathbf{r}{k-1}' \cdot \mathbf{r}{k-1}}{\mathbf{r}{k-2}' \cdot \mathbf{r}{k-2}} \times \mathbf{p}_{k-1}$$


$$a_k = \frac{\mathbf{r}{k-1}' \cdot \mathbf{r}{k-1}}{\mathbf{p}_k' A \mathbf{p}_k}$$
7. $\mathbf{x}k = \mathbf{x}{k-1} + a_k \mathbf{p}_k$
8. $\mathbf{r}k = \mathbf{r}{k-1} -a_k A \mathbf{p}_k$
9. 回到步驟 2
(編者註：原文在註解裡)
最後的 $\mathbf{x}_k$ 就是線性系統的估計解。

在實作的時候，我們不用把每個步驟的結果的記錄下來，所以這個演算法可以重新寫成：


令 $x_0 = 0$ 、 $k = 0$ 、 $\mathbf{r}_0 = \mathbf{b}$


執行以下動作（3~9）直到 $\mathbf{r}$ 夠小


$k = k + 1$


若 $k = 1$， $\mathbf{p} = \mathbf{r}$


若 $k &gt; 1$， $$\mathbf{p} = \frac{\mathbf{r} + (\mathbf{r}' \cdot \mathbf{r})}{\mathbf{r}\mathrm{old}' \cdot \mathbf{r}\mathrm{old}} \times \mathbf{p}$$


$$a = \frac{\mathbf{r}' \cdot \mathbf{r}}{\mathbf{p}' A \mathbf{p}}$$


$\mathbf{x} = \mathbf{x} + a \mathbf{p}$


$\mathbf{r}_\mathrm{old} = \mathbf{r}$


$\mathbf{r} = \mathbf{r} - a A \mathbf{p}$


回到步驟 2


(編按：第 2 步應該是使 $\mathbf{r}$ 的 norm 夠小 )
(編者註：原文在註解裡)

請寫一個函式，利用共軛梯度法求解線性系統。函式格式如下：
格式：
[x, e] = conjugate_gradient( A, b, tol )
輸入：
A:   n×n 的矩陣 A
b:   n×1 向量 b
tol: 容許誤差，也就是演算法第 3 步提到的數字
輸出：
x:   n×1 的向量 x，為線性系統的估計解
e:   1×k 的矩陣，記錄每步的誤差，其中 k 為最後花的迴圈數，e(i) = norm(r_i)

%%
tol = 1e-8;
A = gallery('poisson', 4);
b = ones(size(A, 2), 1)*6;
x0 = [5; 7; 7; 5; 7; 10; 10; 7; 7; 10; 10; 7; 5; 7; 7; 5];
e0 = [6*sqrt(8), 4.8, 0];
[x, e] = conjugate_gradient(A, b, tol);
assert(norm(x-x0)/norm(x0) < 1e-8, 'The solution is incorrect!');
assert(norm(e-e0)/norm(e0) < 1e-8, 'The residuals is incorrect!');
p2. Discrete Fourier Transform

離散傅立葉轉換 是很常被運用的一個演算法，他基本上是一個座標轉換，將一個 n 維的直角座標以傅立葉基底來表示。
給一個長度為 $N$ 的向量 $x(n)$, $n=0, 1, ..., (N-1)$，我們用下列的公式來進行轉換：

其中 $i$ 是虛數的單位
要注意到MATLAB的向量是從 1 開始算，所以計算時的係數要注意


Function Prototype
function x_hat = discrete_Fourier( x )


INPUT：
x: 輸入的向量，是一個n×1的向量


OUTPUT：
x_hat: 離散傅立葉變換後的向量，也是n×1的向量

% test suites:
% #1: x=5;
%     goal=5;
% #2: x=[1;2;3];
%     goal=[6;-1.500000000000000 + 0.866025403784439i; -1.500000000000000 - 0.866025403784439i];
%%

your= discrete_Fourier(x);
assert(norm(goal-your)/norm(goal)<1e-12, 'Incorrect answer on Visible Test 1');
p3. RSA Cryptosystem

RSA加密演算法 是最著名的非對稱加密演算法之一，他的非對稱性及安全性建立在大整數因式分解的困難上面。
公鑰與私鑰的產生方法如下：

隨意選擇兩個質數 $p$ 與 $q$，其中 $p$ 不等於 $q$，並令 $n = p \times q$ 。
求 $$r = \phi(n) = \phi(p) \times\phi(q) = (p-1) \times (q-1)$$，其中 $φ$ 為 歐拉函數 。
選擇一個小於 $r$ 且與其互值[質]的整數 $e$ ，找出一個小於 $r$ 的整數 $d$ 使得 $(de) \bmod r = 1$。（當 $r$ 不大的時候，找 $d$ 可嘗試窮舉）

$n$ 跟 $e$ 用作公鑰、$n$ 跟 $d$ 用作私鑰。

令明文為 $P$、密文為 $C$，則加密方法為
$$C = P^e \bmod n$$
而解密方法為
$$P = C^d \bmod n$$

請寫一個函式，給予兩個質數 $p$ 與 $q$、公鑰 $e$ 、及密文 $C$ ，解密出對應的明文。函式格式如下：
格式：
[P, d] = rsa_decipher( C, e, p, q )

輸入：
C:    密文，為一個小於 n 的整數
e:    公鑰，為一個小於 r 的整數
p, q: 兩個不相等的質數（皆不大於 100）

輸出：
P:    明文，為一個小於 n 的整數
d:    私鑰，為一個小於 r 的整數


注：特別注意大次方容易溢位，建議每乘一次就求一次餘數。
%%
p = 3;
q = 17;
e = 5;
C = 42;
P0 = 9;
d0 = 13;
[P, d] = rsa_decipher(C, e, p, q);
assert(P == P0, 'The plaintext is incorrect!');
assert(d == d0, 'The private key is incorrect!');
p4. Robot Simulation

在一個 m×n 的棋盤狀空間中，每個格子皆有一個燈泡，起始狀況下都是關的；另外還有一個機器人，這個機器人可以接受指令並且作出相應的動作。機器人能夠接受以下的指令：

M: 機器人向他面對的方向移動一格，若撞到邊界則保持不動。
L: 機器人轉向他的左邊。
R: 機器人轉向他的右邊。
\: 機器人把它所在位置的燈打開／關閉

空間以矩陣形式表示， 1 表示燈亮、 0 表示燈暗。矩陣的 (1, 1) 位置為左上角、 (m, 1) 為左下角、 (1, n) 為右上角、 (m, n) 為右下角。

請寫一個函式，給予指令模擬機器人的行為：
格式：
[Light, Trace] = robot( m, n, p, q, f, command )
輸入：
m, n: 矩陣大小為 m×n
p, q: 機器人初始位置為 (p, q)
f:    機器人初始面向，1 為右方，2 為下方，3 為左方，4 為上方
command: 長度為 k 的字串，為輸入的指令
輸出：
Light: m×n 的矩陣，記錄燈的亮暗。
Trace: k×2 的矩陣，記錄機器人的路徑（不含初始位置），Trace(i, :) 為第 i 步的位置。


%%
m = 10;
n = 10;
p = 1;
q = 1;
f = 1;
command = 'M\MM\MMM\LMM\LMMM\LMMMM\RMMM\RMMMM\';
Light0 = [
1 1 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
1 0 0 1 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0];
Trace0 = [
1 2; 1 2; 1 3; 1 4; 1 4; 1 5; 1 6; 1 7;
1 7; 1 7; 1 7; 1 7; 1 7; 1 7; 1 6; 1 5;
1 4; 1 4; 1 4; 2 4; 3 4; 4 4; 5 4; 5 4;
5 4; 5 3; 5 2; 5 1; 5 1; 5 1; 4 1; 3 1;
2 1; 1 1; 1 1];
[Light, Trace] = robot(m, n, p, q, f, command);
assert(isequal(Light, Light0), 'The light matrix is incorrect');
assert(isequal(Trace, Trace0), 'The trace is incorrect');
p5. Golden Ratio Base

我們日常生活用的是十進位，電腦基本的運算與溝通則使用二進位跟十六進位。
這裡，我們來看看這個 黃金進位。 他是將數以黃金比例 φ 的次方和來表示，然後與二進位一樣，係數只有 0 跟 1。 能夠只有 0 和 1 是因為下列這個式子：

在標準的表示式中，不能有連續兩位數是1，這是因為我們有下列這個式子

連接的網頁中有一些整數的黃金進位表示法。

這題要你們做的是黃金進位兩個正數的加法，它的作法蠻直接的，就是把兩個數直接相加後，再將結果以上面兩個關係式轉為標準式即可。 舉例來說：

提示: 可以使用 num2str 這個函式來幫助你尋找小數點的位置，使用的時候請將percision 這參數設為 16 ，不然會有轉換不精確的問題。


Function Prototype
function result = golden_plus(x,y)


INPUT：
x,y: 要進行加法的兩個數，以黃金進位的標準式表示，為 double 型態


OUTPUT：
result: 加法完的結果，請以黃金進位的標準式表示，為 double 型態

Solutions

%%% p1 %%%
function [x, e] = conjugate_gradient( A, b, tol )
  x = b * 0;
  k = 0;
  r = b;
  r_old = r;
  e = [];

  while (norm(r) > tol)
    k = k + 1;
    if k == 1
      p = r;
    else
      p = r + (r' * r) / (r_old' * r_old) * p;
    end

    a = (r' * r) / (p' * A * p);
    x = x + a * p;
    r_old = r;
    r = r - a * A * p;

    e(k) = norm(r);
  end
end
%%% p2 %%%
function x_hat = discrete_Fourier(x)
  x_hat = x .* 0;
  len = length(x);
  for j = 1:len
    for n = 1:len
      x_hat(j) = x_hat(j) + exp(-i*2*pi*(n-1)*(j-1)/len) * x(n);
    end
  end
end
%%% p3 %%%
function [P, d] = rsa_decipher( C, e, p, q )
  n = p * q;
  r = (p-1) * (q-1);
  d = 1
  while mod(d*e, r) ~= 1
    d = d + 1
  end
  P = 1;
  for i = 1:d
    P = mod(P * mod(C, n), n);
  end
end
%%% p4 %%%
function [Light, Trace] = robot( m, n, p, q, f, command )
  k = length(command);
  % RDLU
  x = p;
  y = q;
  Light = zeros(m, n);
  Trace = zeros(k, 2);

  for i = 1:k
    switch command(i)
      case 'M'
        [x, y] = go_forward(x, y, m, n, f);
      case 'L'
        f = mod(f - 2, 4) + 1;
      case 'R'
        f = mod(f, 4) + 1;
      case '\'
        Light(x, y) = mod(Light(x, y) + 1, 2);
    end
    Trace(i, :) = [x, y];
  end
end

function [newx, newy] = go_forward(x, y, m, n, f)
  M = [0, 1; 1, 0; 0, -1; -1, 0];
  newx = x + M(f, 1);
  newy = y + M(f, 2);
  if newx <= 0 || newx > m || newy <= 0 || newy > n
    newx = x;
    newy = y;
  end
end
%%% p5 %%%
% Translated from my solution of http://hoj.twbbs.org.tw/judge/problem/view/52,
% the code is here: https://gist.github.com/andy0130tw/abacb0404da4e4b58856
function result = golden_plus(x, y)
  [ma, mb, mas, mbs] = split_dec(x);
  [na, nb, nas, nbs] = split_dec(y);
  kas = max(mas, nas) + 3;
  kbs = max(mbs, nbs) + 3;
  ma = fillstr(ma, kas, 1);
  na = fillstr(na, kas, 1);
  mb = fillstr(mb, kbs, 0);
  nb = fillstr(nb, kbs, 0);
  ka = ma + na - 2 * '0';
  kb = mb + nb - 2 * '0';
  golden = gold([ka, kb]);
  result = sum(golden .* 10 .^ (kas-1:-1:0));
end

function [c1, c2, s1, s2] = split_dec(num)
  str = strsplit(num2str(num, 16), '.');
  c1 = str{1};
  s1 = length(c1);
  if length(str) > 1
    c2 = str{2};
    s2 = length(c2);
  else
    c2 = '';
    s2 = 0;
  end
end

function rtn = fillstr(str, k, wh)
  strf = repmat('0', 1, k - length(str));
  if wh == 1
    rtn = [strf str];
  else
    rtn = [str strf];
  end
end

function rtn = gold(arr)
  len = length(arr);
  for i = 1:len
    if(arr(i) >= 2)
      if i == len
        arr(len)   = arr(len) - 2;
        arr(len-1) = arr(len-1) + 1;
      elseif i == len-1
        arr(len-1) = arr(len-1) - 2;
        arr(len)   = arr(len) + 1;
        arr(len-2) = arr(len-2) + 1;
      elseif (arr(i-1) == 0 && arr(i+1) == 0)
        arr(i)   = arr(i) - 2;
        arr(i+2) = arr(i+2) + 1;
        arr(i-1) = arr(i-1) + 1;
      end
    end
  end

  ok = 0;
  while ~ok
    for i = 1:len
      if arr(i) >=1 && arr(i-1) >= 1
        arr(i) = arr(i) - 1;
        arr(i-1) = arr(i-1) - 1;
        arr(i-2) = arr(i-2) + 1;
      end
    end

    ok = 1;
    for i = 1:len
      if(arr(i)>1 || (arr(i)>=1 && arr(i-1) >= 1))
        ok = 0;
      end
    end
  end

  rtn = arr;
end
FIN


2015/9/7