This code is GPL

main.js

const PitchDetector = require('./module');

const pd = new PitchDetector(1000);
console.log(pd);

module.ts

/*
*      _______                       _____   _____ _____  
*     |__   __|                     |  __ \ / ____|  __ \ 
*        | | __ _ _ __ ___  ___  ___| |  | | (___ | |__) |
*        | |/ _` | '__/ __|/ _ \/ __| |  | |\___ \|  ___/ 
*        | | (_| | |  \__ \ (_) \__ \ |__| |____) | |     
*        |_|\__,_|_|  |___/\___/|___/_____/|_____/|_|     
*                                                         
* -------------------------------------------------------------
*
* TarsosDSP is developed by Joren Six at IPEM, University Ghent
*  
* -------------------------------------------------------------
*
*  Info: http://0110.be/tag/TarsosDSP
*  Github: https://github.com/JorenSix/TarsosDSP
*  Releases: http://0110.be/releases/TarsosDSP/
*  
*  TarsosDSP includes modified source code by various authors,
*  for credits and info, see README.
* 
*/

/**
 */
/**
 * <p>
 * Implementation of The McLeod Pitch Method (MPM). It is described in the
 * article <a href=
 * "http://miracle.otago.ac.nz/tartini/papers/A_Smarter_Way_to_Find_Pitch.pdf"
 * >A Smarter Way to Find Pitch</a>. According to the article:
 * </p>
 * <blockquote> <bufferCount>
 * <p>
 * A fast, accurate and robust method for finding the continuous pitch in
 * monophonic musical sounds. [It uses] a special normalized version of the
 * Squared Difference Function (SDF) coupled with a peak picking algorithm.
 * </p>
 * <p>
 * MPM runs in real time with a standard 44.1 kHz sampling rate. It operates
 * without using low-pass filtering so it can work on sound with high harmonic
 * frequencies such as a violin and it can display pitch changes of one cent
 * reliably. MPM works well without any post processing to correct the pitch.
 * </p>
 * </bufferCount> </blockquote>
 * <p>
 * For the moment this implementation uses the inefficient way of calculating
 * the pitch. It uses <code>O(Ww)</code> with W the window size in samples and w
 * the desired number of ACF coefficients. The implementation can be optimized
 * to <code>O((W+w)log(W+w))</code> by using an <abbr
 * title="Fast Fourier Transform">FFT</abbr> to calculate the <abbr
 * title="Auto-Correlation Function">ACF</abbr>. But I am still afraid of the
 * dark magic of the FFT and clinging to the familiar, friendly, laggard time
 * domain.
 * </p>
 * 
 * @author Phillip McLeod
 * @author Joren Six
 */

/**
	 * The expected size of an audio buffer (in samples).
	 */
const DEFAULT_BUFFER_SIZE: u32 = 1024;

/**
	 * Overlap defines how much two audio buffers following each other should
	 * overlap (in samples). 75% overlap is advised in the MPM article.
	 */
const DEFAULT_OVERLAP: u32 = 768;

/**
	 * Defines the relative size the chosen peak (pitch) has. 0.93 means: choose
	 * the first peak that is higher than 93% of the highest peak detected. 93%
	 * is the default value used in the Tartini user interface.
	 */
const DEFAULT_CUTOFF: f64 = 0.97;
/**
	 * For performance reasons, peaks below this cutoff are not even considered.
	 */
const SMALL_CUTOFF: f64 = 0.5;

/**
	 * Pitch annotations below this threshold are considered invalid, they are
	 * ignored.
	 */
const LOWER_PITCH_CUTOFF: f64 = 80.0; // Hz
export default class PitchDetector {
	/**
	 * Defines the relative size the chosen peak (pitch) has.
	 */
	private cutoff: f64;

	/**
	 * The audio sample rate. Most audio has a sample rate of 44.1kHz.
	 */
	private sampleRate: f32;

	/**
	 * Contains a normalized square difference function value for each delay
	 * (tau).
	 */
	private nsdf: Float32Array;

	/**
	 * The x and y coordinate of the top of the curve (nsdf).
	 */
	private turningPointX: f32;
	private turningPointY: f32;

	/**
	 * A list with minimum and maximum values of the nsdf curve.
	 */
	private maxPositions: Array<u32> = [];

	/**
	 * A list of estimates of the period of the signal (in samples).
	 */
	private periodEstimates: Array<f32> = [];

	/**
	 * A list of estimates of the amplitudes corresponding with the period
	 * estimates.
	 */
	private ampEstimates: Array<f32> = [];
	/**
	 * Create a new pitch detector.
	 * 
	 * @param audioSampleRate
	 *            The sample rate of the audio.
	 * @param audioBufferSize
	 *            The size of one audio buffer 1024 samples is common.
	 * @param cutoffMPM
	 *            The cutoff (similar to the YIN threshold). In the Tartini
	 *            paper 0.93 is used.
	 */
	constructor(
		audioSampleRate: f32,
		audioBufferSize: u32 = DEFAULT_BUFFER_SIZE,
		cutoffMPM: f64 = DEFAULT_CUTOFF
	) {
		this.sampleRate = audioSampleRate;
		this.nsdf = new Float32Array(audioBufferSize);
		this.cutoff = cutoffMPM;
	}

	/**
	 * Implements the normalized square difference function. See section 4 (and
	 * the explanation before) in the MPM article. This calculation can be
	 * optimized by using an FFT. The results should remain the same.
	 * 
	 * @param audioBuffer
	 *            The buffer with audio information.
	 */
	private normalizedSquareDifference(audioBuffer: f32[]) {
		for (let tau = 0; tau < audioBuffer.length; tau++) {
			let acf: f32 = 0;
			let divisorM: f32 = 0;
			for (let i = 0; i < audioBuffer.length - tau; i++) {
				acf += audioBuffer[i] * audioBuffer[i + tau];
				divisorM +=
					audioBuffer[i] * audioBuffer[i] +
					audioBuffer[i + tau] * audioBuffer[i + tau];
			}
			this.nsdf[tau] = 2 * acf / divisorM;
		}
	}

	/*
	 * (non-Javadoc)
	 * 
	 * @see be.tarsos.pitch.pure.PurePitchDetector#getPitch(f32[])
	 */
	public getPitch(audioBuffer: f32[]) {
		// 0. Clear previous results (Is this faster than initializing a list
		// again and again?)
		this.maxPositions = [];
		this.periodEstimates = [];
		this.ampEstimates = [];

		// 1. Calculate the normalized square difference for each Tau value.
		this.normalizedSquareDifference(audioBuffer);
		// 2. Peak picking time: time to pick some peaks.
		this.peakPicking();

		let highestAmplitude: f64 = -Infinity;
		for (let i = 0; i < this.maxPositions.length; i++) {
			const tau = this.maxPositions[i];
			// make sure every annotation has a probability attached
			highestAmplitude = Math.max(highestAmplitude, this.nsdf[tau]);

			if (this.nsdf[tau] > SMALL_CUTOFF) {
				// calculates turningPointX and Y
				this.parabolicInterpolation(tau);
				// store the turning points
				this.ampEstimates.push(this.turningPointY);
				this.periodEstimates.push(this.turningPointX);
				// remember the highest amplitude
				highestAmplitude = Math.max(
					highestAmplitude,
					this.turningPointY
				);
			}
		}

		let pitch: f32 | null = null;
		if (this.periodEstimates.length > 0) {
			// use the overall maximum to calculate a cutoff.
			// The cutoff value is based on the highest value and a relative
			// threshold.
			const actualCutoff: f64 = this.cutoff * highestAmplitude;

			// find first period above or equal to cutoff
			let periodIndex: u32 = 0;
			for (let i = 0; i < this.ampEstimates.length; i++) {
				if (this.ampEstimates[i] >= actualCutoff) {
					periodIndex = i;
					break;
				}
			}

			const period: f64 = this.periodEstimates[periodIndex];
			const pitchEstimate: f32 = f32(this.sampleRate / period);
			if (pitchEstimate > LOWER_PITCH_CUTOFF) {
				pitch = pitchEstimate;
			} else {
				pitch = -1;
			}
		}
		return {
			probability: highestAmplitude,
			pitch,
			pitched: pitch != null
		};
	}

	/**
	 * <p>
	 * Finds the x value corresponding with the peak of a parabola.
	 * </p>
	 * <p>
	 * a,b,c are three samples that follow each other. E.g. a is at 511, b at
	 * 512 and c at 513; f(a), f(b) and f(c) are the normalized square
	 * difference values for those samples; x is the peak of the parabola and is
	 * what we are looking for. Because the samples follow each other
	 * <code>b - a = 1</code> the formula for <a
	 * href="http://fizyka.umk.pl/nrbook/c10-2.pdf">parabolic interpolation</a>
	 * can be simplified a lot.
	 * </p>
	 * <p>
	 * The following ASCII ART shows it a bit more clear, imagine this to be a
	 * bit more curvaceous.
	 * </p>
	 * 
	 * <pre>
	 *     nsdf(x)
	 *       ^
	 *       |
	 * f(x)  |------ ^
	 * f(b)  |     / |\
	 * f(a)  |    /  | \
	 *       |   /   |  \
	 *       |  /    |   \
	 * f(c)  | /     |    \
	 *       |_____________________> x
	 *            a  x b  c
	 * </pre>
	 * 
	 * @param tau
	 *            The delay tau, b value in the drawing is the tau value.
	 */
	private parabolicInterpolation(tau: i32) {
		let nsdfa: f32 = this.nsdf[tau - 1];
		let nsdfb: f32 = this.nsdf[tau];
		let nsdfc: f32 = this.nsdf[tau + 1];
		let bValue: f32 = tau;
		let bottom: f32 = nsdfc + nsdfa - 2 * nsdfb;
		if (bottom == 0.0) {
			this.turningPointX = bValue;
			this.turningPointY = nsdfb;
		} else {
			const delta: f32 = nsdfa - nsdfc;
			this.turningPointX = bValue + delta / (2 * bottom);
			this.turningPointY = nsdfb - delta * delta / (8 * bottom);
		}
	}

	/**
	 * <p>
	 * Implementation based on the GPL'ED code of <a
	 * href="http://tartini.net">Tartini</a> This code can be found in the file
	 * <code>general/mytransforms.cpp</code>.
	 * </p>
	 * <p>
	 * Finds the highest value between each pair of positive zero crossings.
	 * Including the highest value between the last positive zero crossing and
	 * the end (if any). Ignoring the first maximum (which is at zero). In this
	 * diagram the desired values are marked with a +
	 * </p>
	 * 
	 * <pre>
	 *  f(x)
	 *   ^
	 *   |
	 *  1|               +
	 *   | \      +     /\      +     /\
	 *  0| _\____/\____/__\/\__/\____/_______> x
	 *   |   \  /  \  /      \/  \  /
	 * -1|    \/    \/            \/
	 *   |
	 * </pre>
	 * 
	 * @param nsdf
	 *            The array to look for maximum values in. It should contain
	 *            values between -1 and 1
	 * @author Phillip McLeod
	 */
	private peakPicking() {
		let pos: i32 = 0;
		let curMaxPos: i32 = 0;

		// find the first negative zero crossing
		while (pos < (this.nsdf.length - 1) / 3 && this.nsdf[pos] > 0) {
			pos++;
		}

		// loop over all the values below zero
		while (pos < this.nsdf.length - 1 && this.nsdf[pos] <= 0.0) {
			pos++;
		}

		// can happen if output[0] is NAN
		if (pos == 0) {
			pos = 1;
		}

		while (pos < this.nsdf.length - 1) {
			if (
				this.nsdf[pos] > this.nsdf[pos - 1] &&
				this.nsdf[pos] >= this.nsdf[pos + 1]
			) {
				if (curMaxPos == 0) {
					// the first max (between zero crossings)
					curMaxPos = pos;
				} else if (this.nsdf[pos] > this.nsdf[curMaxPos]) {
					// a higher max (between the zero crossings)
					curMaxPos = pos;
				}
			}
			pos++;
			// a negative zero crossing
			if (pos < this.nsdf.length - 1 && this.nsdf[pos] <= 0) {
				// if there was a maximum add it to the list of maxima
				if (curMaxPos > 0) {
					this.maxPositions.push(curMaxPos);
					curMaxPos = 0; // clear the maximum position, so we start
					// looking for a new ones
				}
				while (pos < this.nsdf.length - 1 && this.nsdf[pos] <= 0.0) {
					pos++; // loop over all the values below zero
				}
			}
		}
		if (curMaxPos > 0) {
			// if there was a maximum in the last part
			this.maxPositions.push(curMaxPos); // add it to the vector of maxima
		}
	}
}

Hi,
I was comparing results with the python version I have and I noted difference in the results between both versions (the python version was better).
I didn't go deep into the McLeod algorithm, but just by comparing with the python version I saw a problem in the normalizedSquareDifference function.
The changes I made:

• subtracting the mean value of the audioBuffer array
• replacing 2 / divisorM by the acf[0]

Is there a reason of this difference ? or it's a mistake ?
In any case thanks a lot ! Your code helped a lot in my project ;)

So I changed that:

private normalizedSquareDifference(audioBuffer: f32[]) {
	for (let tau = 0; tau < audioBuffer.length; tau++) {
		let acf: f32 = 0;
		let divisorM: f32 = 0;
		for (let i = 0; i < audioBuffer.length - tau; i++) {
			acf += audioBuffer[i] * audioBuffer[i + tau];
			divisorM +=
				audioBuffer[i] * audioBuffer[i] +
				audioBuffer[i + tau] * audioBuffer[i + tau];
		}
		this.nsdf[tau] = 2 * acf / divisorM;
	}
}

To that:

private normalizedSquareDifference(audioBuffer: f32[]) {
	let audioBufferMean:f32 = 0;
	for (let tau = 0; tau < audioBuffer.length; tau++) {
		audioBufferMean += audioBuffer[tau]
	}
	audioBufferMean = audioBufferMean/audioBuffer.length;
	for (let tau = 0; tau < audioBuffer.length; tau++) {
		audioBuffer[tau] -= audioBufferMean;
	}
	
	let acfMax:f32;
	for (let tau = 0; tau < audioBuffer.length; tau++) {
		let acf: f32 = 0;
		for (let i = 0; i < audioBuffer.length - tau; i++) {
			acf += audioBuffer[i] * audioBuffer[i + tau];
		}
		if(tau === 0) {acfMax = acf};
		this.nsdf[tau] = acf/acfMax;
	}
}

And I got much better results.
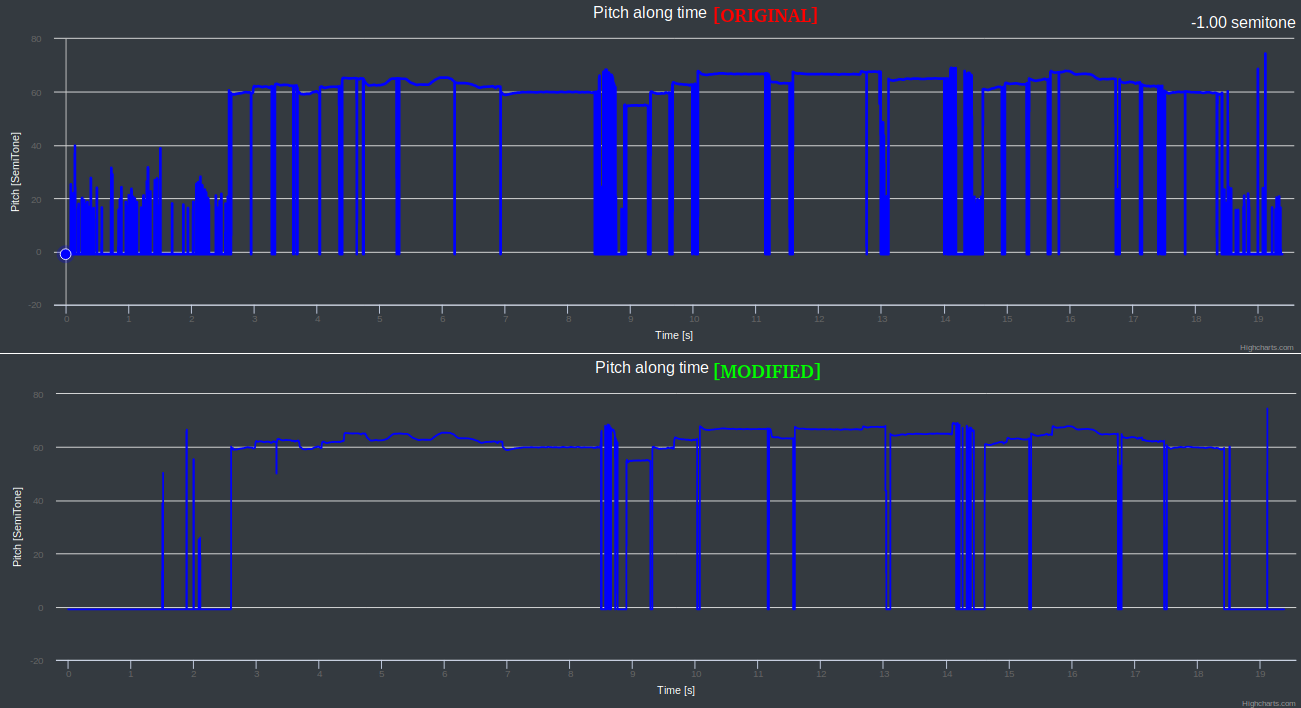
See the difference with an example below on determining the pitch from a short sound.