Last active
December 12, 2023 22:20
-
-
Save ctralie/128cc07da67f1d2e10ea470ee2d23fe8 to your computer and use it in GitHub Desktop.
Greedy Furthest Point Sampling
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| """ | |
| Programmer: Chris Tralie | |
| Purpose: To demonstrate a greedy furthest point sampling, which is a general technique | |
| for getting good points that are "spread out" and cover the dataset well | |
| """ | |
| import numpy as np | |
| import matplotlib.pyplot as plt | |
| from sklearn.metrics.pairwise import pairwise_distances | |
| def getGreedyPerm(D): | |
| """ | |
| A Naive O(N^2) algorithm to do furthest points sampling | |
| Parameters | |
| ---------- | |
| D : ndarray (N, N) | |
| An NxN distance matrix for points | |
| Return | |
| ------ | |
| tuple (list, list) | |
| (permutation (N-length array of indices), | |
| lambdas (N-length array of insertion radii)) | |
| """ | |
| N = D.shape[0] | |
| #By default, takes the first point in the list to be the | |
| #first point in the permutation, but could be random | |
| perm = np.zeros(N, dtype=np.int64) | |
| lambdas = np.zeros(N) | |
| ds = D[0, :] | |
| for i in range(1, N): | |
| idx = np.argmax(ds) | |
| perm[i] = idx | |
| lambdas[i] = ds[idx] | |
| ds = np.minimum(ds, D[idx, :]) | |
| return (perm, lambdas) | |
| def makeVideoExample(): | |
| t = np.linspace(0, 2*np.pi, 101)[0:100] | |
| X1 = np.zeros((len(t), 2)) | |
| X1[:, 0] = np.cos(t) | |
| X1[:, 1] = np.sin(t) | |
| t = np.linspace(0, 2*np.pi, 1001)[0:1000] | |
| X2 = np.zeros((len(t), 2)) | |
| X2[:, 0] = 2*np.cos(t)+5 | |
| X2[:, 1] = 2*np.sin(t) | |
| X3 = np.zeros((len(t), 2)) | |
| X3[:, 0] = 3*np.cos(t) | |
| X3[:, 1] = 3*np.sin(t)+3 | |
| X = np.concatenate((X1, X2, X3), 0) | |
| D = pairwise_distances(X, metric='euclidean') | |
| (perm, lambdas) = getGreedyPerm(D) | |
| xlims = [np.min(X[:, 0]) - lambdas[1], np.max(X[:, 0]) + lambdas[1]] | |
| ylims = [np.min(X[:, 1]) - lambdas[1], np.max(X[:, 1]) + lambdas[1]] | |
| plt.figure(figsize=(8, 4)) | |
| for i in range(50): | |
| plt.clf() | |
| plt.subplot(121) | |
| plt.plot(X[:, 0], X[:, 1], '.') | |
| plt.hold(True) | |
| R = lambdas[i+1] | |
| plt.scatter(X[perm[0:i+1], 0], X[perm[0:i+1], 1], 50, 'k') | |
| t = np.linspace(0, 2*np.pi, 100) | |
| cx = R*np.cos(t) | |
| cy = R*np.sin(t) | |
| for k in range(0, i+1): | |
| plt.plot(cx + X[perm[k], 0], cy + X[perm[k], 1], 'b') | |
| plt.xlim(xlims) | |
| plt.ylim(ylims) | |
| plt.axis('off') | |
| plt.subplot(122) | |
| plt.scatter(X[perm[0:i+1], 0], X[perm[0:i+1], 1]) | |
| plt.xlim(xlims) | |
| plt.ylim(ylims) | |
| plt.axis('off') | |
| plt.savefig("%i.jpg"%i) | |
| if __name__ == '__main__': | |
| makeVideoExample() |
Author
ctralie
commented
May 7, 2018
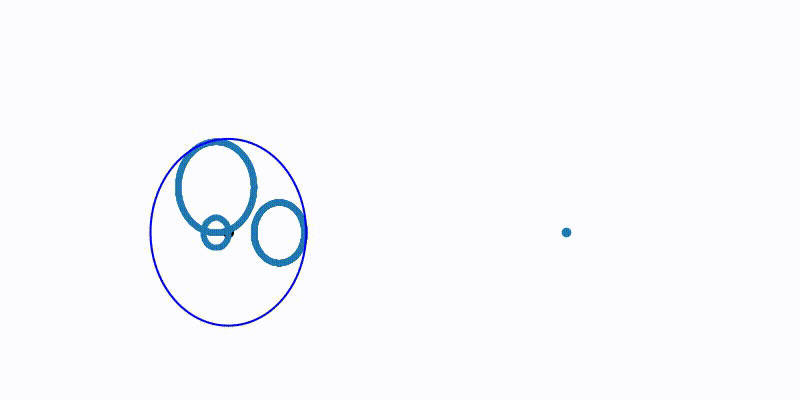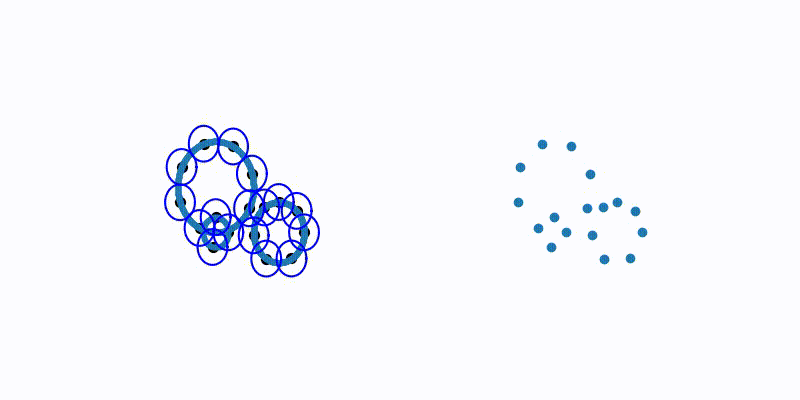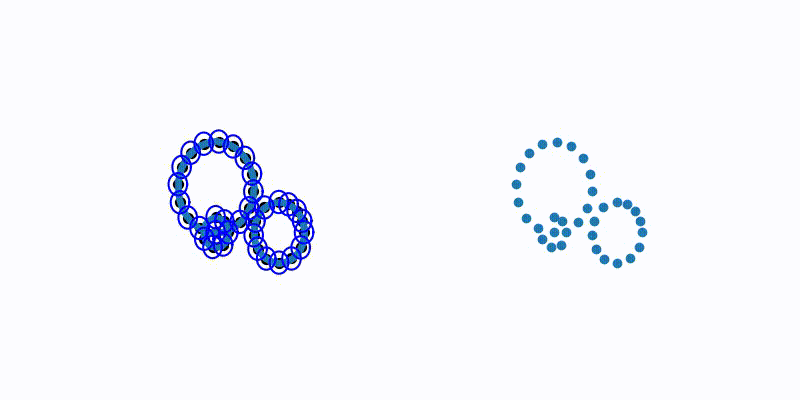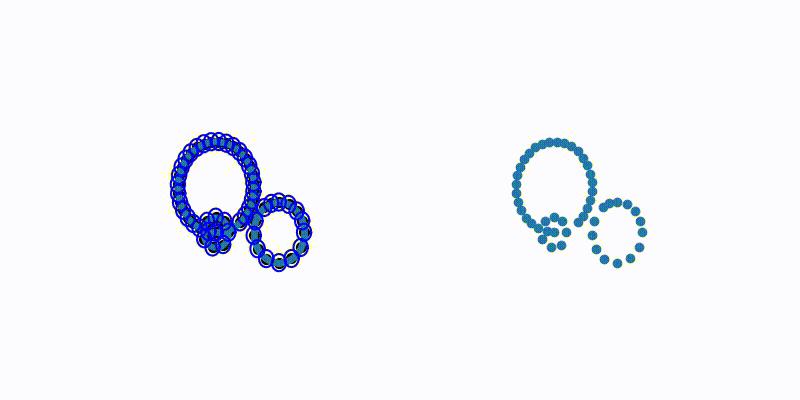
Sign up for free
to join this conversation on GitHub.
Already have an account?
Sign in to comment