Brownian Bridge sample code

brownian_bridge.py

#!/usr/bin/env python                                                                                                                                                                                              

import numpy
import six
from matplotlib import pyplot


seed = 0
N = 100
M = 10

numpy.random.seed(seed)


def sample_path_batch(M, N):
    dt = 1.0 / N
    dt_sqrt = numpy.sqrt(dt)
    B = numpy.empty((M, N), dtype=numpy.float32)
    B[:, 0] = 0
    for n in six.moves.range(N - 1):
        t = n * dt
        xi = numpy.random.randn(M) * dt_sqrt
        B[:, n + 1] = B[:, n] * (1 - dt / (1 - t)) + xi
    return B


B = sample_path_batch(M, N)
pyplot.plot(B.T)
pyplot.show()

This is useful thanks!
Generally, brownian bridge is such that: Z0 = Z1 = 0, which is not true here.
So I suggest amending to:

def sample_path_batch(M, N):
    dt = 1.0 / (N -1)                                                          #  changed from 1.0 / N
    dt_sqrt = numpy.sqrt(dt)
    B = numpy.empty((M, N), dtype=numpy.float32)
    B[:, 0] = 0
    for n in six.moves.range(N - 2):                                           # changed from "for n in six.moves.range(N - 1)"
         t = n * dt
         xi = numpy.random.randn(M) * dt_sqrt
         B[:, n + 1] = B[:, n] * (1 - dt / (1 - t)) + xi
    B[:, -1] = 0                                                               # added: set the last B to Zero
    return B

Which avoids the last B to be truncated as shown in the attached plot.
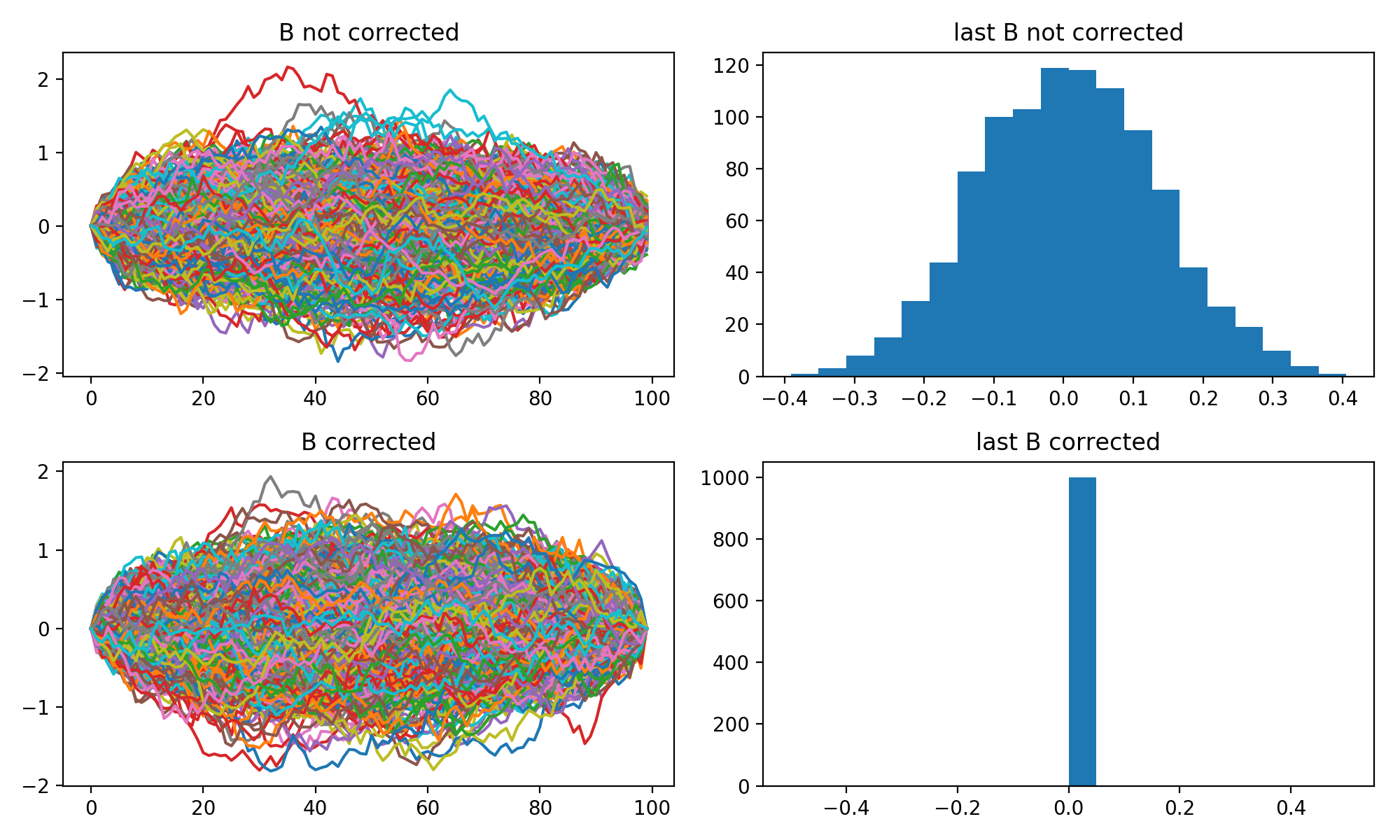
Let me know what you think please.

I was using this code but needed it to work with an arbitrary shape so I made that and thought to share it here

in_shape = (60, 20, 20)
N = 10

def sample_path_batch_shape(N, in_shape):
    dt = 1.0 / (N -1)           
    dt_sqrt = np.sqrt(dt)
    B = np.empty((N,) + in_shape, dtype=np.float32)
    B[0, :, :, :] = 0
    for n in six.moves.range(N - 2):                
         t = n * dt
         xi = np.random.randn(*in_shape) * dt_sqrt
         B[n + 1] = B[n] * (1 - dt / (1 - t)) + xi
    B[-1] = 0                                                 
    return B

I was using this code but needed it to work with an arbitrary shape so I made that and thought to share it here

in_shape = (60, 20, 20)
N = 10

def sample_path_batch_shape(N, in_shape):
    dt = 1.0 / (N -1)           
    dt_sqrt = np.sqrt(dt)
    B = np.empty((N,) + in_shape, dtype=np.float32)
    B[0, :, :, :] = 0
    for n in six.moves.range(N - 2):                
         t = n * dt
         xi = np.random.randn(*in_shape) * dt_sqrt
         B[n + 1] = B[n] * (1 - dt / (1 - t)) + xi
    B[-1] = 0                                                 
    return B

You inspire me that a brownian bridges with arbitrary boundary condition may be an interesting problem.