Given the specific parameters (size, wall, start and target), you should build a virtual block map. If the size is 10, then it will be a 10x10 blocks map. Each block is numbered sequentially from left to right, then top to bottom. The initial value for this sequence is 1.
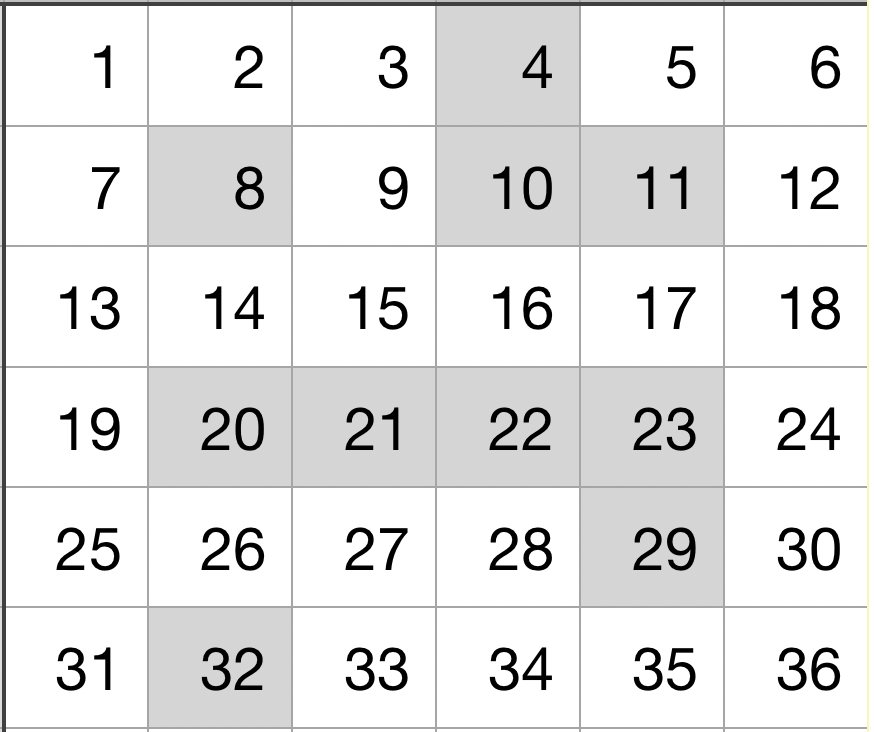
If the size value is 6, then the map will be like this,
All numbers in the wall value are considered as walls on the map, according to the matched block number. Consider the wall value is 4,8,10,11,20,21,22,23,29,32, then the map will have walls (let's assume they're the grey blocks) like this,
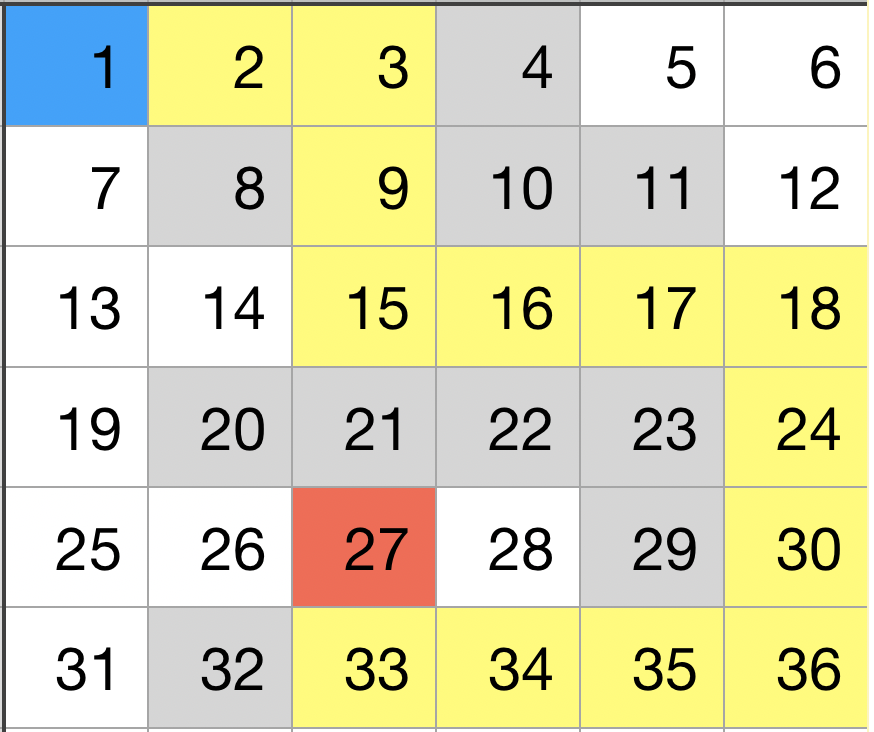
If we set the start value to 1 and the target value to 27 then now we have a maze challenge like this,
The program should be able to find the fastest path from the start to the target. Only up, down, left and right moves are allowed, no diagonal move at all.
This path below may be a correct path to the target, but not the fastest one,
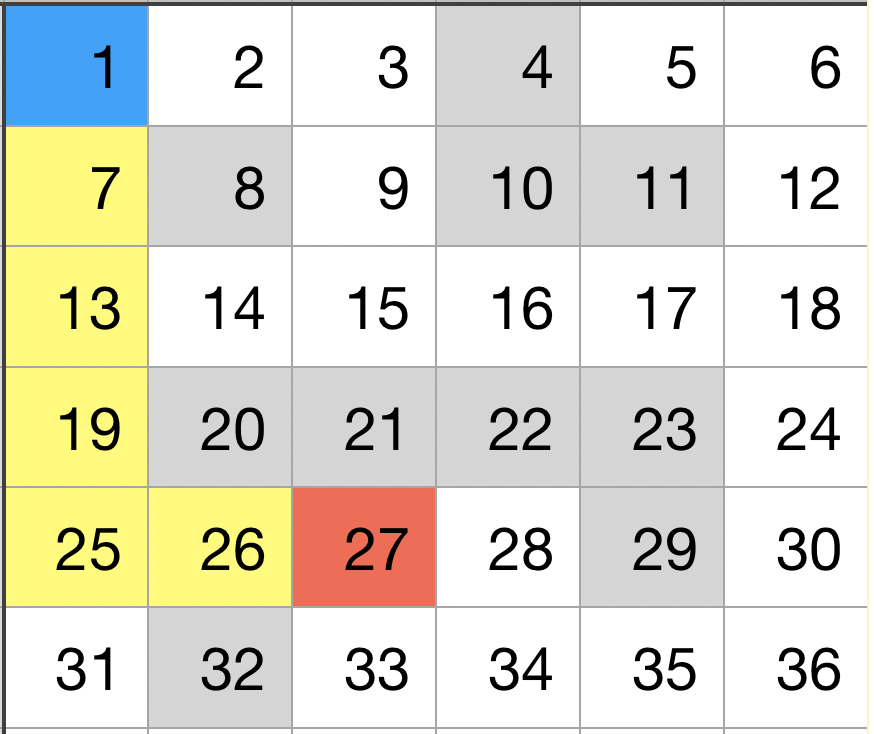
This is the correct and the fastest path,
In this case, the result of the program should be 7,13,19,25,26.
sizeintegerwallstring (comma separated)startintegertargetinteger
size: 10 <= x <= 100wall: 1 <= x <= (size*size)start:start⊄wall,start: 1 <= x <= (size*size)target:target⊄wall,target: 1 <= x <= (size*size)
Array of block numbers that represents the solution from the start to target target (written in the comma separated string).
size: 20wall:1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,23,24,27,31,32,36,40,41,43,44,45,49,54,56,57,58,60,,61,63,67,68,69,70,71,72,74,75,76,80,81,83,85,87,91,92,96,98,99,100,101,105,107,108,109,112,114,120,121,123,124,125,127,131,134,135,136,137,139,140,141,142,143,147,149,154,159,160,161,163,165,166,167,169,170,172,174,176,178,179,180,181,183,185,190,192,196,197,199,200,201,206,207,210,212,213,214,217,220,221,222,223,224,230,231,232,237,238,240,241,245,246,247,248,250,252,254,255,260,261,263,268,270,275,277,278,279,280,281,283,284,285,290,291,292,293,297,300,301,305,307,308,309,310,313,316,317,318,320,321,322,323,325,332,333,334,338,340,341,343,345,347,349,350,352,356,357,358,360,361,365,368,369,374,380.381,382,383,384,385,386,387,388,389,380,381,382,383,384,385,386,387,389,390,391,392,393,394,395,396,397,398,399,400start: 23target: 298
22,42,62,82,102,103,104,84,64,65,66,46,47,48,28,29,30,50,51,52,53,73,93,113,133,153,173,193,194,195,215,235,236,256,276,296,295,315,335,355,375,376,377,378,379,359,339,319,299



Case 2 (fuad)
1,2,3,4,5,6,7,8,9,10,11,20,22,23,24,25,26,27,29,30,31,33,34,38,40,44,45,47,48,49,51,53,54,55,56,58,62,64,66,67,69,70,71,73,75,77,78,88,89,90,91,93,94,95,96,97,98,99,100,111,112,113,114,115,116,117,118,119,120,12112,13,14,15,16,17,28,39,50,61,72,83,82,81,92,103,104,105,106,107,108,109,110