Permute with Python - Audience: Beginner, Intermediate

README-Template.md

Permutations using Python

One simple program using Python for applying strings and integer permutations.
The following gist offers a program scaled in four subsets:

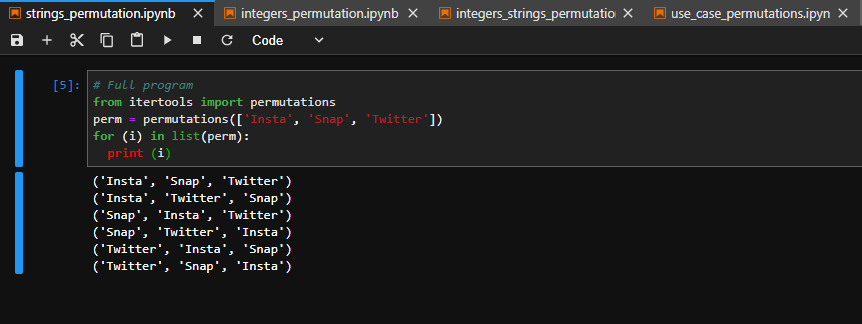
• apply permutations on strings, refer to strings_permutation.py
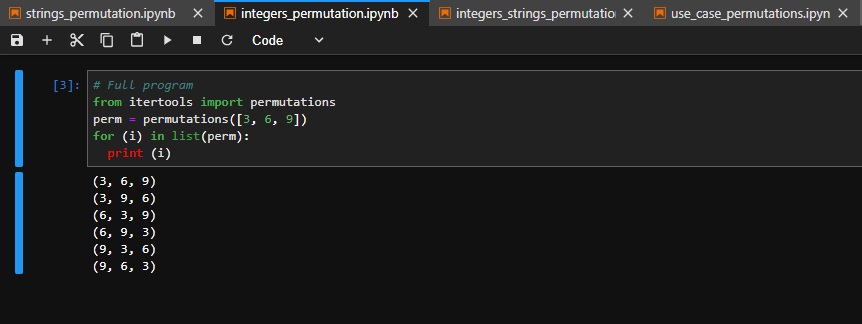
• apply permutations on integers, refer to integers_permutation.py
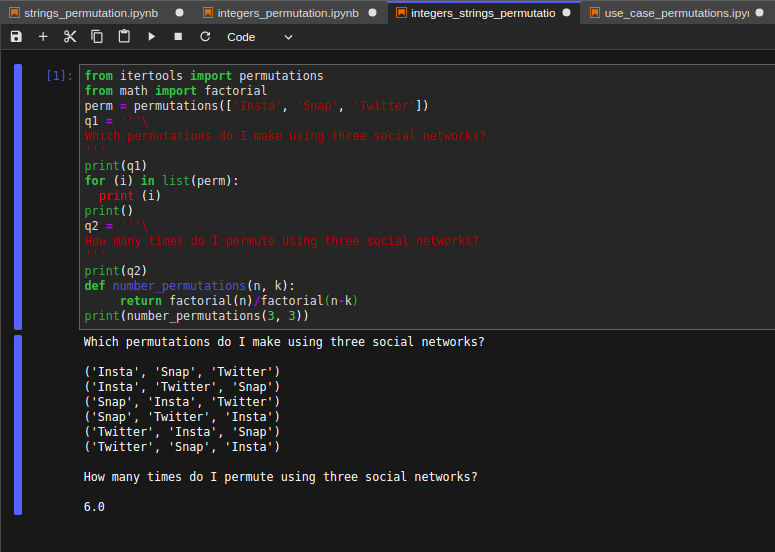
• apply permutations on both integers and strings in a single program, refer to integers_strings_permutation.py
• use case: apply permutations on a card game, refer to use_case_permutations.py.

Getting Started

This Python program built in four lines helps you avoid the use of an extented code for applying permutations on numeric data. The below instructions will help you run this Python program on your local machine for development and testing purposes, as well as in third party sites hosted in the cloud.

• (#) and (''') are used to comment the following gist.

Prerequisites

I am using Jupyter Notebook on localhost (Ubuntu 18.04 bionic).
Make sure to have Jupyter Notebook installed on your operating system or launch it on remote servers (see Tips).

Tips

If you are not using Linux/Unix and still want to try this simple Python program:

• use https://labs.cognitiveclass.ai (create a free account, then click on "JupyterLab" in the Build Analytics section)
• use https://dataplatform.ibm.com (recommended for IBM Coders)

Basic commands in Jupyter Notebook

• Note that in Jupyter you add new lines by typing "b" from your keyboard whilst the notebook is opened.
• Avoid runing the entire code in a single cell in order to understand the steps.
• Use "ctrl + enter" to execute each line if you want to get the output.
• Use "dd" outside a cell to delete it.
• Running the last cell should execute the permutations as program output.

Whilst your Jupyter Notebook is open... Use this line of code in your first cell

from itertools import permutations

'''
This loads requested package
and library in your notebook
'''

Use this line of code in your second cell

perm = permutations([3, 6, 9])

'''
This returns no result until
the last cell is ran
'''

Use this line of code in your third cell

for (i) in list(perm): 
print (i)

'''
This completes the program, showing permutations
of numbers 3,6,9 as output.
'''

Running the tests

• I used Ubuntu (18.04 bionic) to launch Jupyter Notebook on localhost.
• Localhost instantiates while using $ jupyter notebook in the terminal.
• Check if Jupyter is correctly installed: $ jupyter --version

Built With

• Jupyter - An open source software for creating notebooks
• Itertools - Functions creating iterators for efficient looping
• Math - Mathematical functions defined by the C standar

Versioning

I used no vesioning system for this gist, which repos status is flagged as concept because it is intended to be a demo or POC (proof-of-concept).

Author

• Isaac Arnault - Suggesting a minified code from Initial work redspider

License

All public gists https://gist.github.com/isaacarnault
Copyright 2018, Isaac Arnault
MIT License, http://www.opensource.org/licenses/mit-license.php

Use case - Applying a factorial n function in a card game

Extended application of the above program. Permutations are great for finding number of ways an array of integers can be sorted. Let's imagine that that we have a standard 52-card deck and we wish to find the number of permutations of four aces while shuffling the cards. We may need to add a function to our code and to use another package and libraby. Check use_case_permutations.py for more info.

integers_permutation.py

# Calling the requested package and library
from itertools import permutations 

# Defining permutations array of integers
perm = permutations([3, 6, 9]) 

# Requesting the program output
for (i) in list(perm): 
  print (i) 

# Full program
from itertools import permutations
perm = permutations([3, 6, 9])    
for (i) in list(perm):
  print (i)

integers_strings_permutation.py

# Calling two packages and a related library per each
from itertools import permutations
from math import factorial

# Defining permutations array of strings
perm = permutations(['Insta', 'Snap', 'Twitter']) 

# Requesting the program to ask a question (q1) and print the result (program will compile the array of strings)
q1 = '''\ 
Which permutations do I make using three social networks?
'''
print(q1)
for (i) in list(perm):
  print (i)
  
# Removing print() from your program will just remove the blank line between both questions without affecting the entire program
print() 

# Requesting the program to ask a question (q2) and print the result (program will compile the array of integers)
q2 = '''\
How many times do I permute using three social networks?
'''
print(q2)
def number_permutations(n, k):
     return factorial(n)/factorial(n-k)
print(number_permutations(3, 3))

# Full program
from itertools import permutations
from math import factorial
perm = permutations(['Insta', 'Snap', 'Twitter']) 
q1 = '''\
Which permutations do I make using three social networks?
'''
print(q1)
for (i) in list(perm):
  print (i)
print() 
q2 = '''\
How many times do I permute using three social networks?
'''
print(q2)
def number_permutations(n, k):
     return factorial(n)/factorial(n-k)
print(number_permutations(3, 3))

LICENSE

MIT License

Copyright (c) 2018 Isaac Arnault

Permission is hereby granted, free of charge, to any person obtaining a copy
of this software and associated documentation files (the "Software"), to deal
in the Software without restriction, including without limitation the rights
to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
copies of the Software, and to permit persons to whom the Software is
furnished to do so, subject to the following conditions:

The above copyright notice and this permission notice shall be included in all
copies or substantial portions of the Software.

THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
SOFTWARE.

OUTPUT.md

Ignore below outputs if programs ran correctly.
If you begin in Python using Jupyter these are what you should get:

• apply permutations on strings, see strings_permutation.py

strings_permutation

# Full program
from itertools import permutations
perm = permutations(['Insta', 'Snap', 'Twitter'])    
for (i) in list(perm):
  print (i)

• apply permutations on integers, see integers_permutation.py

integers_permutation

# Full program
from itertools import permutations
perm = permutations([3, 6, 9])    
for (i) in list(perm):
  print (i)

• apply permutations on both integers and strings in a single program, see integers_strings_permutation.py

integers_strings_permutation

# Full program
from itertools import permutations
from math import factorial
perm = permutations(['Insta', 'Snap', 'Twitter']) 
q1 = '''\
Which permutations do I make using three social networks?
'''
print(q1)
for (i) in list(perm):
  print (i)
print() 
q2 = '''\
How many times do I permute using three social networks?
'''
print(q2)
def number_permutations(n, k):
     return factorial(n)/factorial(n-k)
print(number_permutations(3, 3))

• use case: apply permutations on a card game, see use_case_permutations.py

use_case_permutations

# Full program
from math import factorial
def number_permutations(n, k):
    return factorial(n)/factorial(n-k)
q = '''\
How many times can 4 aces from a standard 52-card deck
permutate while I shuffle the cards?
'''
print(q)
print(number_permutations(52, 4))

strings_permutation.py

# Calling the requested package and library
from itertools import permutations 

# Defining permutations array of strings
perm = permutations(['Insta', 'Snap', 'Twitter']) 

# Requesting the program output
for (i) in list(perm): 
  print (i) 

# Full program
from itertools import permutations
perm = permutations(['Insta', 'Snap', 'Twitter'])    
for (i) in list(perm):
  print (i)

use_case_permutations.py

# Calling the requested package and library
from math import factorial
def number_permutations(n, k):
  
# Defining permutations array of k items from a set of size n using the algorithm n!/(n-k)!
return factorial(n)/factorial(n-k)
q = '''\
How many ways can 4 aces from a standard 52-card deck
permutate while I shuffle the cards?
'''   
    
# Requesting the program output
print(q)
print(number_permutations(52, 4))

# Full program
from math import factorial
def number_permutations(n, k):
    return factorial(n)/factorial(n-k)
q = '''\
How many times can 4 aces from a standard 52-card deck
permutate while I shuffle the cards?
'''
print(q)
print(number_permutations(52, 4))