Last active
May 21, 2021 13:00
-
-
Save janhuenermann/3d7c95deb1e5f9081d65159e826f6c4f to your computer and use it in GitHub Desktop.
Find the smallest rotated rectangle that covers a given polygon
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| import numpy as np | |
| # Gift wrapping algorithm, from https://en.wikipedia.org/wiki/Gift_wrapping_algorithm | |
| def find_convex_hull(poly): | |
| """ | |
| Returns the convex hull of the given polygon | |
| Can be replaced using OpenCV: | |
| ``` | |
| hull = cv2.convexHull(poly, clockwise=True, returnPoints=False) | |
| return poly[hull[:, 0]] | |
| ``` | |
| """ | |
| n = len(poly) | |
| p_i = p_0 = np.argmin(poly[:, 0]) | |
| hull = [] | |
| while p_i != p_0 or len(hull) == 0: | |
| hull.append(p_i) | |
| p_e = 0 | |
| # For each vertex, test if p_j is left of line between p_i <-> p_e | |
| for p_j in range(n): | |
| if p_e == p_i or np.cross(poly[p_e], poly[p_j] - poly[p_i]) > np.cross(poly[p_i], poly[p_j]): | |
| p_e = p_j | |
| p_i = p_e | |
| return np.array([poly[k] for k in hull]) | |
| def find_min_rotated_rect(poly): | |
| """Returns the four points of the smallest rotated rect that covers the given poly""" | |
| ch = find_convex_hull(poly) | |
| edges = ch - np.roll(ch, 1, 0) | |
| edges = edges / np.linalg.norm(edges, 2, -1)[:, None] | |
| normals = np.stack((-edges[:, 1], edges[:, 0]), 1) | |
| basis = np.stack((edges, normals), -1) | |
| ps = np.matmul(ch, basis) | |
| ps0 = np.amin(ps, 1) | |
| ps1 = np.amax(ps, 1) | |
| areas = np.prod(ps1 - ps0, -1) | |
| k = np.argmin(areas) | |
| rotated_rect = np.array( | |
| [[ps0[k, 0], ps0[k, 1]], | |
| [ps0[k, 0], ps1[k, 1]], | |
| [ps1[k, 0], ps1[k, 1]], | |
| [ps1[k, 0], ps0[k, 1]]]) | |
| return rotated_rect @ basis[k].T |
Here's another test case
poly = np.zeros((n, 2))
for i in range(1, n):
poly[i] = poly[i-1] + np.random.normal(size=(2,)) * 0.33
poly[:, 0] = 1. * (poly[:, 0] - np.min(poly[:, 0])) / (np.max(poly[:, 0]) - np.min(poly[:, 0])) - .5
poly[:, 1] = 1. * (poly[:, 1] - np.min(poly[:, 1])) / (np.max(poly[:, 1]) - np.min(poly[:, 1])) - .5
rect = find_min_rotated_rect(poly)
rect = norm_rect_with_ll_point(rect, poly)
plot_poly(poly)
plot_poly(rect)
plt.xlim(-1., 1.)
plt.ylim(-1., 1.)
plt.scatter(poly[0, 0], poly[0, 1])
plt.scatter(rect[0, 0], rect[0, 1])
plt.grid('on')
plt.show()And an animated version of the outputs:
Sign up for free
to join this conversation on GitHub.
Already have an account?
Sign in to comment
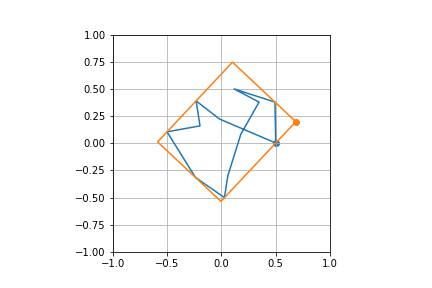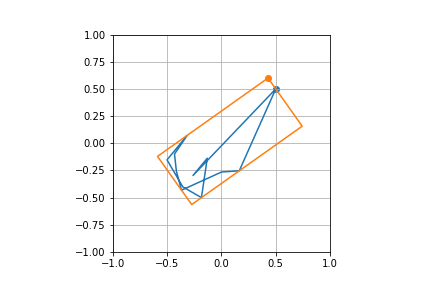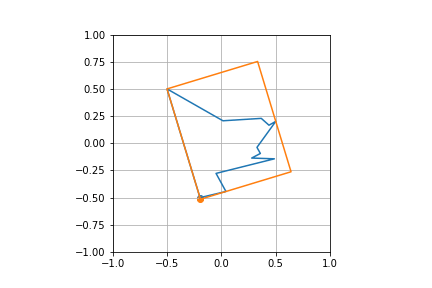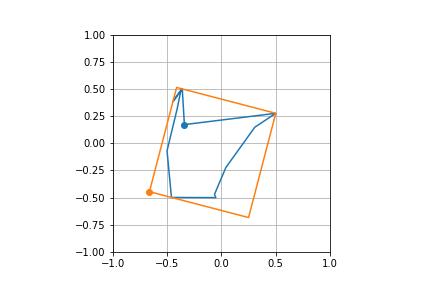
Test cases