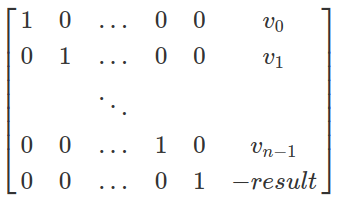Короче, ███████, я тебя [ДАННЫЕ УДАЛЕНЫ] и в благородство играть не буду. Достанешь для меня флаг — и мы [ДАННЫЕ УДАЛЕНЫ].
- challenge.sage
- output.txt
Нам выдаётся файл с кодом challenge.sage и его выходные данные output.txt. Рассмотрим подробнее, что делает код.
1. Сначала флаг и ключ шифрования читаются из файлов и передаются в функцию encrypt(), результат которой затем печатается:
def main():
flag = read_file('flag.txt')
key = read_file('key.txt')
result = encrypt(flag, key)
print(result)2. Сама функция encrypt() только разбивает входные данные на блоки. Можно сделать вывод, что шифр — блочный, размер блока указан выше:
N = 16
def encrypt(plaintext, key):
assert len(plaintext) == len(key)
ciphertext = []
for i in range(0, len(plaintext), N):
plaintext_block = plaintext[i:i+N]
key_block = key[i:i+N]
ciphertext_block = encrypt_block(plaintext_block, key_block)
ciphertext.append(ciphertext_block)
return ciphertextdef encrypt_block(plaintext, key):
assert len(plaintext) == len(key) == N
t = ceil(mean(plaintext + key)) ^ 3
q = next_prime(t + randint(0, t))
pol = construct_polynomial(q, plaintext, key)
ciphertext = encrypt_polynomial(pol)
return q, ciphertextСначала она вычисляет какие-то параметры t и q, а затем строит многочлен на основе блоков флага и ключа.
Здесь и далее используются специфичные для SageMath объекты, но их суть может быть понятна из названия. Например, зная, что plaintext и key — блоки байтов длины N, можно понять, что mean() вычисляет среднее арифметическое всех этих байтов, а ceil(), соответственно, округляет результат вверх. Полученное число t используется для вычисления q — простого числа, чуть большего, чем t. Вероятно, это нужно, чтобы найти какое-либо простое число q, которое будет гарантированно больше, чем все символы во флаге и ключе (но к этому мы ещё вернёмся).
4. Посмотрим в функцию construct_polynomial(), чтобы понять, как составляется многочлен от флага и ключа:
def construct_polynomial(q, plaintext, key):
F = GF(q)
P.<x> = PolynomialRing(F)
Q.<x> = P.quo(x^N - 1)
r, s = map(Q, map(list, [plaintext, key]))
return (r / s).lift().change_ring(ZZ)GF(q) — это конечное поле размера q. Затем над этим полем строится кольцо многочленов, то есть множество всех многочленов, коэффициенты которых лежат в поле GF(q). Следующая строчка P.quo(x^N - 1) означает, что все операции с многочленами мы будем проводить по модулю многочлена x^N - 1.
Мы получили Q — кольцо многочленов, коэффициенты которого не больше q, а сами многочлены не больше x^N - 1. Затем из блоков флага и ключа получаются многочлены r и s: символы используются как коэффициенты. После всего этого мы делим r / s и получаем другой многочлен, коэффициенты которого переводятся в ZZ — обычные целые числа.
5. Теперь у нас есть многочлен pol. Посмотрим в функци encrypt_polynomial(), чтобы понять как он преобразовывается:
from math import cos
R = RealField(4096)
def encrypt_polynomial(pol):
values = [R(cos(z)) for z in pol]
keystream = [R(1 + z).sin() for z in range(pol.degree() + 1)]
return sum(k * v for k, v in zip(keystream, values))В начале создаётся R — поле действительных чисел с точностью 4096 бит. Действительные числа могут быть бесконечно близко к нулю, поэтому для того, чтобы их хранить в компьютере, может потребоваться бесконечное количество бит. При создании поля можно указать, как много бит числа мы хотим хранить (то есть насколько маленьким оно может быть).
Затем с использованием тригонометрических функций создаются два массива. Сначала вычисляется массив values, в котором i-ый элемент равен косинусу i-ого коэффициента многочлена pol. Далее вычисляется ещё один массив — keystream, в котором элементы равны синусам последовательных чисел от 1 до N + 1 (потому что степень многочлена pol.degree() равна N).
После всего вычисляется скалярное произведение полученных массивов, оно и возвращается функцией как результат шифрования одного блока.
Теперь, когда мы разобрали код, пришло время придумать алгоритм решения.
Заметим, что синусы вычисляются у элементов поля методом R.sin(), следовательно, точность полученных чисел будет равна 4096 бит. В отличие от них, косинусы вычисляются встроенной в Python функцией math.cos(), которая работает с типом float и возвращает результат с точностью всего 64 бита. Получается, что элементы values содержат сильно меньше битов данных, чем элементы keystream.
Здесь аналогичная ситуация. У многочленов r и s коэффициенты не больше 8 бит (так как это байты), а размер поля GF(q) в три раза больше: примерно 24 бита. Это вызвано тем, что простое число q примерно равно третьей степени от входных байтов:
t = ceil(mean(plaintext + key)) ^ 3
q = next_prime(t + randint(0, t))Выходит, что коэффициенты r и s тоже содержат сильно меньше бит данных, чем размер поля q.
Когда мы встречаемся с ситуацией, когда что-то сильно меньше другого, на ум приходит алгоритм LLL, который уже не первое десятилетие успешно взламывает многие криптографические алгоритмы.
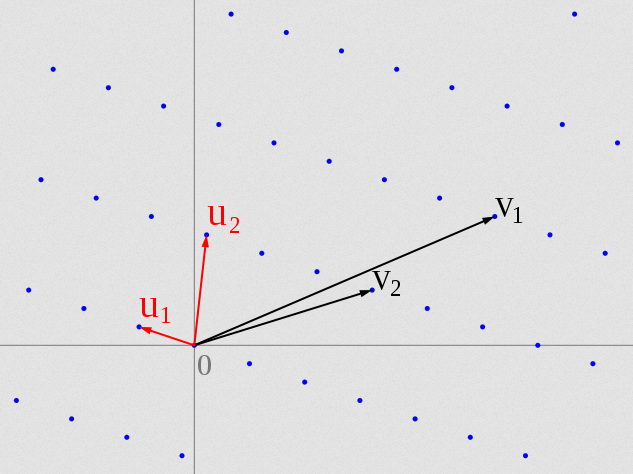
LLL умеет находить кратчайчайший почти ортогональный базис решётки. Что это значит?
Если говорить простыми словами, то решётка — это набор каких-то векторов, которые можно складывать между собой и получать новые вектора. Базис решётки — это множество таких векторов решётки, которые мы никак не можем получить, как бы мы ни складывали другие вектора. Базис решётки образует векторное пространство, при этом одно и то же пространство можно задавать разными базисами:
На рисунке выше видно, что базисы (u1, u2) и (v1, v2) образуют одно и то же пространство, но базис (u1, u2) короче и ортогональнее. В данном случае, если бы мы запустили LLL на базисе (v1, v2), он бы смог редуцировать его до (u1, u2).
Мы можем использовать LLL, чтобы из результата работы функции encrypt_polynomial() (всего одного вещественного числа!) достать массив values — коэффициенты секретного многочлена pol, в котором спрятан флаг. Это возможно из-за того, что неизвестные числа (values) по размеру сильно меньше, чем известные (keystream). Под размером здесь имеется в виду размер в битах, то есть количество информации.
Эта задача похожа на частный случай задачи о сумме подмножеств с низкой плотностью, которую LLL умеет эффективно решать. В теории решёток подобная задача называется задачей нахождения кратчайшего вектора (SVP). Нужно помнить, что LLL не умеет работать с вещественными числами, поэтому их нужно перевести в целые, например, умножив на 2^4096. А затем перевести обратно.
Пример решётки:
Здесь v_i — это числа из массива keystream, а result — результат скалярного произведения.
В этом случае нам нужно решить задачу рационального восстановления. Существует лемма Тью, которая утверждает, что для восстановления t = r / s (mod q) необходимо выполнение условия r * s < q / 2. Теперь понятно, зачем q создавалось примерно третьей степени от элементов (пункт 3).
Тот факт, что коэффициенты многочленов r и s сильно меньше, чем порядок всего поля q, позволяет нам снова использовать LLL. Похожая атака используется в криптоанализе алгоритма NTRUEncrypt. В статье на Википедии есть пример решётки:
Когда мы получим все многочлены r для каждого блока флага, останется только представить их коэффициенты в виде последовательностей байт и соединить в одну строку. Нужно помнить, что кроме флага в базисе решётки будет содержаться ещё и ключ.
LetoCTF{p0lyn0m1aLLL_overdose!!}