SDDE estimation with Stan

sdde.py

import pystan

try:
    model  # avoid recompiling during IPython/notebook session
except:
    model = pystan.StanModel('sdde.stan')

data = dict(
    nt=500,
    d=50,
    dt=0.1,
    I=0.1234,
    K=-1.0,
    eta_sd=0.5,
    obs_sd=0.5,
)

run = model.sampling(data=data, iter=500, warmup=250)

samp = run.extract()
xth = samp['x_t_hat'].mean(axis=0)

figure(figsize=(15, 15))
subplot(211);
plot(xth);
title('X(t) inferred')

subplot(223); hist(samp['K_hat'], 100); title('True K=-1.0');
subplot(224); hist(samp['I_hat'], 100); title('True I=0.1234')

sdde.stan

data {
  int nt; // num time points
  int d; // delay in steps
  real dt; // time step size
  real I; // vertical shift bistable system
  real K; // scale of delay input
  real eta_sd; // scale of SDE noise
  real obs_sd; // scale of observation noise
}

transformed data {
  vector[nt] x_t;
  vector[nt] eta; // noise

  for (t in 1:nt)
    eta[t] = normal_rng(0, 1);

  for (t in 1:d)
    x_t[t] = eta[t];

  for (t in (d + 1):nt)
  {
    real x1 = x_t[t - 1];
    real xd = x_t[t - d];
    real dx = x1 - x1*x1*x1/3.0 + I + K * xd + eta[t]*eta_sd;
    x_t[t] = x1 + dt * dx;
  }
} 

parameters {
  vector[nt] eta_hat;
  real I_hat;
  real K_hat;
}

transformed parameters {
  vector[nt] x_t_hat;

  for (t in 1:d)
    x_t_hat[t] = eta_hat[t];

  for (t in (d + 1):nt)
  {
    real x1 = x_t_hat[t - 1];
    real xd = x_t_hat[t - d];
    real dx = x1 - x1*x1*x1/3.0 + I_hat + K_hat * xd + eta_hat[t]*eta_sd;
    x_t_hat[t] = x1 + dt * dx;
  }
}

model {
  eta_hat ~ std_normal();
  I_hat ~ std_normal();
  K_hat ~ std_normal();
  x_t ~ normal(x_t_hat, obs_sd);
}

sdde2.py

import numpy as np
import pylab as pl
import pystan

try:
    model
except:
    model = pystan.StanModel('sdde2.stan')

dt=0.2
data = dict(
    nt=250,
    nh=50,
    dmu=50*dt,
    dsd=10*dt,
    dt=dt,
    I=0.1234,
    K=-0.5,
    eta_sd=0.5,
    obs_sd=0.5,
    debug=0,
)

run = model.sampling(data=data, iter=2000, warmup=1000, chains=4)
samp = run.extract()

pl.figure()
pl.subplot(211);
pl.plot(samp['x_t_hat'].mean(axis=0));
pl.title('X(t) inferred')

pl.subplot(234); pl.hist(samp['K_hat'], 100); pl.title(f'True K={data["K"]}');
pl.subplot(235); pl.hist(samp['I_hat'], 100); pl.title(f'True I={data["I"]}')
pl.subplot(236); pl.hist(samp['dhat'], 100); pl.title(f'True d={data["dmu"]}')

sdde2.stan

data {
  int nt; // num time points
  int nh; // num history for t<0
  real dmu; // delay prior mean
  real dsd; // delay prior std
  real dt; // time step size
  real I; // vertical shift bistable system
  real K; // scale of delay input
  real eta_sd; // scale of SDE noise
  real obs_sd; // scale of observation noise
}

transformed data {
  vector[nt] x_t = rep_vector(0.0, nt);
  vector[nt] eta; // noise
  vector[nt] ts; // times
  real w_norm = 1.0 / (dsd * sqrt(2.0 * pi()));

  for (t in 1:nt)
  {
    eta[t] = normal_rng(0, 1);
    ts[t] = dt * t;
  }

  x_t[1:nh] = eta[1:nh];
  for (t in (nh + 1):nt)
  {
    real x1 = x_t[t - 1];
    vector[nt] wt = w_norm * exp(-0.5 * square((ts - (t*dt - dmu))/dsd));
    real dx = x1 - x1*x1*x1/3.0 + I + K * (wt' * x_t) + eta[t]*eta_sd;
    x_t[t] = x1 + dt * dx;
  }
}

parameters {
  vector[nt] eta_hat;
  real I_hat;
  real K_hat;
  real<lower=0> dhat;
}

transformed parameters {
  vector[nt] x_t_hat = eta_hat;
  for (t in (nh + 1):nt)
  {
    real x1 = x_t_hat[t - 1];
    vector[nt] wt = w_norm * exp(-0.5 * square((ts - (t*dt - dhat))/dsd));
    real dx = x1 - x1*x1*x1/3.0 + I_hat + K_hat * (wt' * x_t_hat) + eta_hat[t]*eta_sd;
    x_t_hat[t] = x1 + dt * dx;
  }
}

model {
  eta_hat ~ std_normal();
  I_hat ~ std_normal();
  K_hat ~ std_normal();
  dhat ~ std_normal();
  x_t ~ normal(x_t_hat, obs_sd);
}

sdde3.jl

dt=0.1
nt=500
nh=100
dmu=100*dt
dsd=30*dt
dt=dt
I=0.1234
K=-0.5
eta_sd=0.5
debug=0

x_t = zeros(nt)
eta = zeros(nt)
ts = zeros(nt)
w_norm = 1.0 / (dsd * sqrt(2.0 * pi))
sqrt_dt = sqrt(dt)

for t=1:nt
    eta[t] = randn()
    ts[t] = dt * t
end

function square(x) x * x end

x_t[1:nh] = eta[1:nh]
for t=(nh + 1):nt
    x1 = x_t[t - 1]
    wt = @. w_norm * exp(-0.5 * square((ts - (t*dt - dmu)) / dsd))
    dx = x1 - x1*x1*x1 / 3.0 + I + K * (wt' * x_t)
    x_t[t] = x1 + dt * dx + sqrt_dt * eta[t] * eta_sd
end


using Turing, Plots, StatsPlots

@model sdde3(dsd, dmu, x_t, w_norm, ts, dt, eta_sd) = begin
    I_hat ~ Normal(0, 1)
    K_hat ~ Normal(0, 1)
    dhat ~ Normal(0, 1)
    dhat_ = dhat / dsd + dmu + dsd;
    for t=(nh + 1):nt
        x1 = x_t[t - 1]
        wt = @. w_norm * exp(-0.5 * square((ts - (t*dt - dhat_)) / dsd))
        dx = x1 - x1*x1*x1 / 3.0 + I_hat + K_hat * (wt' * x_t)
        # @show x1, dt, dx
        x_t[t] ~ Normal(x1 + dt * dx, eta_sd::Float64)
    end
end

run = sample(sdde3(dsd, dmu, x_t, w_norm, ts, dt, eta_sd), NUTS(), 1000)
@show describe(run)
@show I, K, dmu

plot(run)

sdde3.py

import numpy as np
import pylab as pl
import pystan

try:
    model
except:
    model = pystan.StanModel('sdde3.stan')

dt=0.1
data = dict(
    nt=500,
    nh=100,
    dmu=100*dt,
    dsd=30*dt,
    dt=dt,
    I=0.1234,
    K=-0.5,
    eta_sd=0.5,
    debug=0,
)


run = model.sampling(data=data, iter=2000, warmup=1000, chains=4)
samp = run.extract()

pl.figure()
pl.subplot(211);
pl.plot(samp['x_t_'].mean(axis=0));
pl.title('X(t)')

pl.subplot(234); pl.hist(samp['K_hat'], 100); pl.title(f'True K={data["K"]}');
pl.subplot(235); pl.hist(samp['I_hat'], 100); pl.title(f'True I={data["I"]}')
pl.subplot(236); pl.hist(samp['dhat_'], 100); pl.title(f'True d={data["dmu"]}')

sdde3.stan

data {
  int nt; // num time points
  int nh; // num history for t<0
  real dmu; // delay prior mean
  real dsd; // delay prior std
  real dt; // time step size
  real I; // vertical shift bistable system
  real K; // scale of delay input
  real eta_sd; // scale of SDE noise
}

transformed data {
  vector[nt] x_t = rep_vector(0.0, nt);
  vector[nt] eta; // noise
  vector[nt] ts; // times
  real w_norm = 1.0 / (dsd * sqrt(2.0 * pi()));
  real sqrt_dt = sqrt(dt);

  for (t in 1:nt)
  {
    eta[t] = normal_rng(0, 1);
    ts[t] = dt * t;
  }

  x_t[1:nh] = eta[1:nh];
  for (t in (nh + 1):nt)
  {
    real x1 = x_t[t - 1];
    vector[nt] wt = w_norm * exp(-0.5 * square((ts - (t*dt - dmu))/dsd));
    real dx = x1 - x1*x1*x1/3.0 + I + K * (wt' * x_t);
    x_t[t] = x1 + dt * dx + sqrt_dt*eta[t]*eta_sd;
  }
}

parameters {
  real I_hat;
  real K_hat;
  real dhat;
}

transformed parameters {
  // shift to have slightly wrong prior
  real dhat_ = dhat/dsd + dmu + dsd;
}

model {
  I_hat ~ std_normal();
  K_hat ~ std_normal();
  dhat ~ std_normal();
  for (t in (nh + 1):nt)
  {
    real x1 = x_t[t - 1];
    vector[nt] wt = w_norm * exp(-0.5 * square((ts - (t*dt - dhat_))/dsd));
    real dx = x1 - x1*x1*x1/3.0 + I_hat + K_hat * (wt' * x_t);
    x_t[t] ~ normal(x1 + dt * dx, eta_sd);
  }
}

generated quantities {
  vector[nt] x_t_ = x_t; // too lazy to recode sim in Python!
}

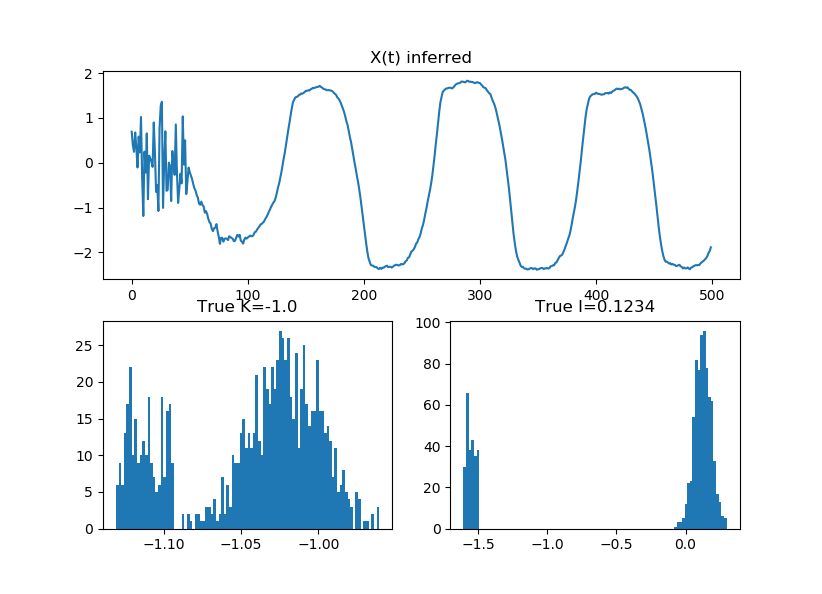
Added second variant for estimating delay but doesn't initialize properly (yet)

Fixed the temporal kernel in the second variant, so it runs now. It's significantly more expensive 💻 🛫 than the first one, but it estimates delay.

Added 3rd variant which doesn't have an observation model or estimate noise, and it's considerably faster. This suggests the 2nd variant could be better constrained to behave nicely.

with the 3rd variant (sdde3.stan) where delay is recovered correctly despite wrong prior.

Added a Julia version with Turing.jl which sort of works but unlikely to be optimal.