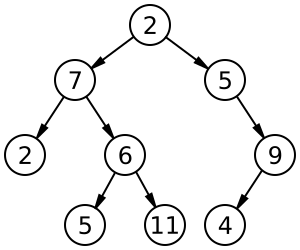
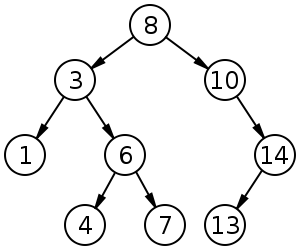
Trees are a type of data structure consisting of nodes and links to other nodes. Each tree starts with a node called the root node. This node has zero or more child nodes which in turn may also have zero or more child nodes. From this we can see that trees can be thought of as recursive data structures - each node can be thought of as its own tree. Furthermore, trees cannot have cycles - that is, a child node cannot link back to its parent (or any other ancestor), and nodes can have exactly one parent node. In general nodes can have any number of child nodes, but for our discussion we'll focus on a binary tree or a tree where nodes can have at most 2 children.
Source: Wikipedia
We often work with trees by defining a tree node class, containing at least two variables - value, and a link to the node's children (in our case, we'll call these children left and right, since we're working with a binary tree).
class TreeNode:
def init(self, x):
value = x
left = None
right = None
Some problems lend themselves to a tree structure - think of something with a predecessor and several possible outcomes for example. We also use trees because it can make searching for something much faster. For example, we can use something called a binary search tree to find nodes in O(log n) time. A binary search tree arranges nodes in a very particular way - all nodes in the left subtree of any given node must be less than or equal to the value of that given node, and all nodes in the right subtree must be greater. This ordering allows us to quickly move through the tree, eliminating about half the possibilities at each step.
Source: Wikipedia
One note of caution with this approach - we can only eliminate about half of the nodes if the tree is roughly balanced. Technically the tree on the left is a binary search tree, but if we were to search through it we would only be able to eliminate one node at a time. If we were searching for 6, the left tree would take 6 checks to tell if it was in the tree, while the right tree would only require 3 checks.
Source: http://venus.cs.qc.cuny.edu/~mfried/cs313/self_balancing_trees.html
The most important thing to know when using a tree is how to navigate through it. If you're able to master this you'll be able to search through trees to manipulate them in many ways. There are two common ways of traversing trees - using Depth First Search or using Breadth First Search. DFS works by going down into the tree as deeply as possible before backtracking up, while BFS goes broadly - it searches every node on a level before going to the next level. There are three common ways traveling through trees using DFS, and they can all be written very succinctly using recursion.
When using In-Order traversal on a binary search tree one visits the nodes in ascending order. We do this recursively by first checking the left child, then the current node, then the right child.
def inOrder(node):
if node is not None:
inOrder(node.left)
print(node.value)
inOrder(node.right)
In pre-order traversal we visit the current node first, then the left and right children (hence, the "pre" in the name).
def preOrder(node):
if node is not None:
print(node.value)
preOrder(node.left)
preOrder(node.right)
In post-order traversal we visit the current node last, hence the "post" in the name.
def postOrder(node):
if node is not None:
postOrder(node.left)
postOrder(node.right)
print(node.value)
Using these traversal methods we can iterate through the entire tree, which is useful if we need to make changes to the tree, or if we want to look at every node. We'll explore Breadth First Search in the practice problems.
Trees can be challenging, especially for beginners, but they can be a very powerful data structure. It can be helpful to think of trees as a recursive data structure - each node (and it's subtree) can be considered its own tree. Thinking of trees in this way can help you arrive at an answer when you're trying to solve problems using trees. Using stacks and queues can also help you order the nodes in a way that help solve your problems.
Try implementing a solution to a problem using both recursive and iterative methods to really solidify your knowledge!
Given a Binary Search Tree, return the node with the minimum data. Example:
4
/ \
2 8
/ \
5 10
Output: The tree node containing 2
Follow up: Could you find the maximum node as well? (Output of above example would be 10.)
Write a function to find the total number of leaf nodes in a binary tree. A node is described as the leaf node if it doesn't have any children. If there are no leaf nodes, return 0. Example:
1
/ \
2 3
/ \ / \
4 5 6 7
/ \
8 9
Output: 5
Write a function to iteratively determine the total number of "full nodes" in a binary tree. A full node contains left and right child nodes. If there are no full nodes, return 0.
1
/ \
2 3
/ \ / \
4 5 6 7
/ \
8 9
Output: 4
Given a binary tree, return the level order traversal of its nodes' values. (ie, from left to right, level by level).
For example:
3
/ \
9 20
/ \
15 7
return its level order traversal as: [ [3], [9,20], [15,7] ]
Invert a binary tree.
Example:
Input:
4
/ \
2 7
/ \ / \
1 3 6 9
Output:
4
/ \
7 2
/ \ / \
9 6 3 1
Given a binary tree, determine if it is a valid binary search tree (BST).
Assume a BST is defined as follows:
The left subtree of a node contains only nodes with keys less than the node's key. The right subtree of a node contains only nodes with keys greater than the node's key. Both the left and right subtrees must also be binary search trees. Example 1:
Input:
2
/ \
1 3
Output: true
Example 2:
5
/ \
1 4
/ \
3 6
Output: false
Explanation: The input is: [5,1,4,null,null,3,6]. The root node's value is 5 but its right child's value is 4.
Given a binary tree, find its maximum depth.
The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node. A leaf is a node with no children.
Example: Given binary tree:
3
/ \
9 20
/ \
15 7
return its depth = 3.
Given a non-empty binary tree, return the average value of the nodes on each level in the form of an array. Example 1: Input:
3
/ \
9 20
/ \
15 7
Output: [3, 14.5, 11] Explanation: The average value of nodes on level 0 is 3, on level 1 is 14.5, and on level 2 is 11. Hence return [3, 14.5, 11].
We are given the head node root of a binary tree, where every node's value is either a 0 or a 1. Return the same tree where every subtree not containing a 1 has been removed. (Recall that the subtree of a node X is X, plus every node that is a descendant of X.) The value of each node will only be 0 or 1.
Example: Input:
1
\
0
/ \
0 1
Output:
1
\
0
\
1
Given a binary search tree, write a function to find the kth smallest element in it. You may assume that k is always valid, 1 <= k <= BST's total elements.
Gist content by Mary Troiani for presentation given at the Algorithms and Technical Interview Study Group - May 22, 2018 meetup
This is a part of a series of presentations for Learn Teach Code - Algorithm Study Group