-
-
Save noamross/4638544 to your computer and use it in GitHub Desktop.
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Noam Ross | |
| --------- | |
| ### 13-01-22 14:50:15 | |
| Abstract | |
| ======== | |
| Forest disease spreads through plant communities structured by species composition, age distribution, and spatial arrangement. I propose to examine the consequences of the interaction of these components of population structure on a model systems of *Phytophthora ramorum* invasion in California redwood forests. First, I will compare the dynamic behavior of a series of epidemiological models that include different configurations of population structures. Then I will fit these models to time-series data from a network of disease monitoring plots to determine what components of forest population structure are most important for prediction of disease spread. Using the most parsimoniuous models, I will determine optimal schedules of treatment to minimize the probability of disease outbreak. | |
| Introduction: Modeling Disease in Complex Populations for Management | |
| ==================================================================== | |
| Forest diseases can radically transform ecosystems. In North America, chestnut blight, Dutch elm disease and beech bark disease have caused precipitous declines in their hosts, leading to changes in the structure and function of forests. Changes from such diseases may be the dominant force changing the face of some forests in coming decades, overwhelming other forms of rapid environmental change such as climate change (Lovett et al. 2006). | |
| Even simple host-disease systems exhibit complex dynamics (Kermack and Mckendrick 1927). Forest disease dynamics include additional complexity driven by variation in pathogen and host populations, spatial strucure, pathogen life cycles, and demographic and environmental stochasticity (Hansen and Goheen 2000, Holdenrieder et al. 2004). These factors yield greater complexity in disease dynamics. This complexity, combined with limited monitoring data and the uncertainty of the parameters of emergent diseases, makes prediction of disease dynamics difficult. Yet such prediction is needed decision-making in allocating limited resources for treatment and prevention. | |
| One area of complexity in forest systems is structured variation in host populations. Host tree populations may consist of multiple species or genotypes, and consist of multiple sizes, each of which may interact with disease or each other differently (Gilbert and Hubbell 1996). All forest tree populations are spatially structured; non-motile individuals can not be "well-mixed" (Filipe and Maule 2003). Each of these forms of population structure have consequences for population dynamics that have been examined in theoretical models (Park et al. 2001, 2002, Dobson 2004, Klepac and Caswell 2010). However, dynamics resulting from these components of population structure interacting are not well-characterized. | |
| Understanding modeled dynamics of disease in structured populations may provide insights useful for management. However, the ability to use such models for management planning depends requires confidence in their predictive power, particularly under novel management treatments. Recent developments in *particle filter* techniques allow estimation of the likelihoods of complex dynamic models (Arulampalam et al. 2002, Ionides et al. 2006, Knape and de Valpine 2012), and subsequent comparison of models in out-of-sample predictive performance (Vehtari and Ojanen 2012). Fitting the dynamic models in full provides more confidence in the dynamic results than deriving madel parameters individually from data, because it tests whether models' emergent dynamics are supported by the data. | |
| Modeling multidimensional population structure is problematic for several reasons. First, as models get increasingly complex, analytic solutions are less likely to be tractable, and complete characterization of model behavior is unlikely. Thus model (and) system behavior is more difficult to explore. Secondly, high-dimensional models are difficult to estimate; each additional form of population structure multiplies the parameters involved, and requires additional data. | |
| Sudden oak death (SOD) is an emerging forest disease in California and Oregon that threatens populations of tanoak (*Notholithocarpus densiflorus*) (Rizzo and Garbelotto 2003), and has the potential to modify community structure (Metz et al. 2012), and cause significant economic damage (Kovacs et al. 2011). Silvicultural chemical, and other control techniques can modify the progression of disease (Swiecki and Bernhardt 2013), but eradication of SOD is unlikely [@Cobb2013] even at local scales. Long and short- and long-term solutions to limit the damage of disease are needed will require continuous treatment and monitoring regimes. Under budget constraints, planning for such treatment can be informed by dynamics models via optimal control techniques. | |
| I aim to answer the following overall questions: | |
| 1. How do interactions between community, size, and spatial structure affect disease dynamics in forests? | |
| 2. What aspects of population structure are most important in determining the probability and size of forest disease outbreaks in theoretical models? | |
| 3. What aspects of population structure are most important in *predicting* the probability and size of SOD outbreaks? | |
| 4. What population structure minimizes the risk of SOD outbreak while maintaining desirable populations of at-risk species? | |
| 5. What is the most cost-effective strategy for maintaining populations of tree species in the presence of SOD? | |
| Background | |
| ========== | |
| Sudden Oak Death | |
| ---------------- | |
| Sudden Oak Death (SOD) is an emerging forest disease in California and Oregon that poses risks to forest across North America. First observed in California in the mid-1990s, SOD is caused by the water mold *Phytophthora ramorum* (Rizzo et al. 2002). *P. ramorum* often kills tanoak (*Notholithocarpus densiflorus*), which provide habitat and food to many vertebrate species, and are the primary host of ectomycorrhizal fungi in redwood forests (Rizzo and Garbelotto 2003). Loss of this species may have cascading effects on other species. The disease has also caused significant economic damage through removal costs and property value reduction (Kovacs et al. 2011). It has the potential to spread to species in other regions, such as northern red oak (*Quercus rubra*), one of the most important eastern timber species (Rizzo et al. 2002). | |
| Population Structure: Multiple Host Species | |
| ------------------------------------------- | |
| *Phytophthora ramorum* has over 100 host species in 40 genera, which fall into several functional types (Swiecki and Bernhardt 2013). In canker hosts, which are all members of *Fagaceae* in California, pathogen produces cankers in the trunk. Few if any spores are produced from the cankers, and these hosts are generally dead ends. SOD is fatal to many canker costs. In foliar hosts, *P. ramorum* resides and reproduces in leaves and twigs. Foliar hosts vary greatly in suscepibility to disease and spore production from diseased individuals. Some hosts are dead ends; others are major drivers of disease spread and survival. | |
| In Redwood forests in Northern California, the hosts of importance are tanoak and bay laurel (*Umbellularia californica*). Tanoak has the dubious distinction of being the only species that is both a canker and foliar host, and the disease is generally lethal in these trees. Bay laurel is a foliar host in which *P. ramorum* produces prolifically, and it suffers no harm from the disease (DiLeo et al. 2009). Redwood and other species are unsusceptible or dead-end hosts where *P. ramorum* has little detrimental effect. In forests of the redwood-tanoak-bay complex, bay Laurel acts as the primary disease reservoir [@Davidso2008]. Tanoak infection and mortality is dependent on bay laurel density (Cobb et al. 2012), and removal of laurel is a commonly suggested treatment to reduce risk of SOD (@Filipe2013; Swiecki and Bernhardt 2013). | |
| Dobson (2004) examined a model of disease in multiple host species based on an the SIR (Kermack and Mckendrick 1927) framework. In it, species had density dependence but interacted only though disease transmission. Importantly, transmission between species was always equal or less than transmission between species. Dobson found that in when transmission was density-dependent, species had a complementary effect on the disease's rate of reproduction "); that is, a mix of both species led to faster outbreaks. However, in frequency-dependent case,  was greatest when one species dominated. Transmission between species dampens and synchronizes disease oscillations in each species, and at very high contact rates between species the most susceptible species are more like to go extinct. Craft and Hawthorne (2008) implemented a stochastic version of this model in a system of mamallian carnivores, finding that species with low intra-species contact rates acted as sinks for disease, and their contact with more social species increased spread disease within these low-contact species. | |
| SOD dynamics differ from these systems in a few important ways. First, the contact structure among species may not be symmetrical, and between-species contacts may be as high as within. Contact rates in this case are driven by differences in species transmissivity (amount of spore produced) and susceptibility (probability of infection per spore) rather than social grouping. Where one species with high transmissivity coexists with a species of high susceptibility, the probability of transmission may be higher between species than within. Also, the spatial structure of species, and the dispersal pattern of spores, may result in a hybrid between density and frequency-dependent disease transmissions. | |
| Population Structure: Size/Stage Classes | |
| ---------------------------------------- | |
| Within the tanoak population, epidemiological characteristics vary with tree size. Trees of larger size classes are more likely to be infected and die more quickly than smaller tree (Cobb et al. 2012), Possibly due to the vulnerability of cracked bark and the amount of bark tissue available for invasion (Swiecki and Bernhardt 2005). There is no evidence currently for differences in spore production or other physiological effecst across tree sizes [@Davidson2008]. | |
| When disease dynamics occur much faster than demographic processes, we can treat size classes similarly to different species, and examine the progression of disease in a constant population structure. However, when disease progression and growth occur at similar rates, these processes can interact to produce complex dynamics. This is the case with SOD; infectious periods can last many years, during which trees may continue to grow. | |
| The effects of age-based population structure and contact rates have been studied extensively in the context of human disease and vaccination programs (Anderson and May 1985, ). Reducing in-class transmission rates at young ages increases the average age of infection, independent of the exact contact structure. When only the susceptibility, and not transmissivity, of each age class varies, | |
| Klepac and Caswell (2010) created a framwork for examining disease dynamics in stage-structured populations. In this, disease and epidemiological processes are alternate in time (TODO: *periodic something*). This approximation holds with SOD in California, where most sporulation occurs during the winter rainy months, while tree growth occurs in the spring and fall [TODO:ref]. | |
| Klepac and Caswell (2010) found that increases in within-class transmission increases both the infected and recovered population, relative increases in that class | |
| Protecting a class drives average age at infection to other classes. If infection is most common in the young, then vaccination increases age to infection. Vaccination in the old will, too, but much less. Accentuates oscillation. ˜ | |
| In SOD, contact rates appear to depend less on mixing rates. But transmissivity varies across species, and suscepibility varies across age classes. | |
| Population Structure: Space | |
| --------------------------- | |
| *P. Ramorum* dispersal interacts with host population structure at many scales. The pathogen spreads between trees via wind-blown rain, and splash, limiting most spores to spread within 15m of host plants (Davidson et al. 2005). However, occaisional weather events, such as fog, can transport spores up to 3 km (Rizzo et al. 2005). Over long distances, *P. ramorum* can be transported in streams or spread via human-mediated vectors such as nursery plant trade [@Osterbauer2004]. Meentemeyer et al. (2011) found that the best fit kernel for *P. ramorum spread* was the sum of two Cauchy kernels, one on the scale of tens of meters and another on the scale of tens of kilometers. | |
| Despite the ability to spread long distance, strong meter-scale gradients mean that individual trees in stands can not be considered "well mixed" in terms of contact rates between trees. Rather, contact patterns across space arise from the interaction of spatial clustering of trees and the dispersal kernel of the disease. Neither frequency- nor density-dependent transmission characterizes this arrangement. | |
| The effect on such spatial structure on development of epidemics has been studied with continuous populations in space [@Bolker1999], metapopulation models (Park et al. (2001); Park et al. (2002)), models of individuals on a lattice (Filipe and Maule 2003, 2004) and discrete individuals in continuous space (Brown and Bolker (2004)). These approaches have reached similar conclusions of the effect of spatial structure in non-mobile populations. In all cases, the threshold of disease growth for a global outbreak ") is greater than the threshold for a local epidemic "). For instance, in metapopulations on a lattice, 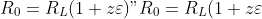"), where  is the average number of connections between patches and  is the inter-patch contact rates (Park et al. 2001). In models of discrete individuals in space, 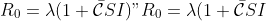"), where  would be the pathogen growth rate in a well-mixed population, and  is the dispersal kernel-weighted spatial correlation between susceptible and infected individuals.  evolves over time but reaches a minimum that represents the threshold required for a global epidemic (Brown and Bolker 2004). Also, both clustering and anti-clustering (oversdispersal) reduce the rate of increase of disease, except when clustering occurs at the scale of dispersal, in which case it can accellerate spread. Fat-tailed dispersal kernels accellerate spread, as well. | |
| Study Approach | |
| ============== | |
| I will examine the comparative importance of these components of population structure by (1) characterizing the dynamic behavior of models that include each type of structure and their combinations and (2) identifying the model structure that best predicts data of disease spread over time in redwood-tanoak-bay forests. Using the best-fit model, I determine optimal paths for silvicultural and stand protection treatments to minimize the risk of outbreak over time | |
| Comparative Dynamics | |
| -------------------- | |
| To characterize the effects of the population structure on disease dynamics, I will compare four models. All are extensions of the epidemiological model of Cobb et al. (2012). | |
| **Model A** is the simplest of the four models, only representing structure in the form of differences between species of trees. It is described by this system of stochastic difference equations: | |
| ![\\begin{aligned} \\boldsymbol{S}\_{t+1} &\\sim \\boldsymbol{S\_t} + \\overbrace{ \\text{Pois}\\left[\\boldsymbol{b(S\_t+I\_t)}\\left(1-\\sum\_{i=1}\^n w\_i (S\_{it} + I\_{it}) \\right) + \\boldsymbol{rm\_I I\_t}\\right]}\^{\\text{new recruits}} - \\overbrace{\\text{Binom}\_1\\left((\\underbrace{1 - e\^{-\\boldsymbol{\\beta I\_t} - \\boldsymbol{\\lambda\_{ex}}}}\_{\\text{force of infection}})\\boldsymbol{S\_t} \\right)}\^{\\text{infections}} -\\overbrace{\\text{Binom}\_2(\\boldsymbol{m\_S S\_t})}\^{\\text{mortality}} \\\\ \\boldsymbol{I}\_{t+1} &\\sim \\boldsymbol{I\_t} + \\text{Binom}\_1\\left((1 - e\^{-\\boldsymbol{\\beta I\_t} - \\boldsymbol{\\lambda\_{ex}}})\\boldsymbol{S\_t} \\right) - \\text{Binom}\_3(\\boldsymbol{m\_I} \\boldsymbol{S\_t}) \\end{aligned}](http://latex.codecogs.com/gif.latex?%5Cbegin%7Baligned%7D%0A%5Cboldsymbol%7BS%7D_%7Bt%2B1%7D%20%26%5Csim%20%5Cboldsymbol%7BS_t%7D%20%2B%20%5Coverbrace%7B%20%20%5Ctext%7BPois%7D%5Cleft%5B%5Cboldsymbol%7Bb%28S_t%2BI_t%29%7D%5Cleft%281-%5Csum_%7Bi%3D1%7D%5En%20w_i%20%28S_%7Bit%7D%20%2B%20I_%7Bit%7D%29%20%5Cright%29%20%2B%20%5Cboldsymbol%7Brm_I%20I_t%7D%5Cright%5D%7D%5E%7B%5Ctext%7Bnew%20recruits%7D%7D%20-%20%5Coverbrace%7B%5Ctext%7BBinom%7D_1%5Cleft%28%28%5Cunderbrace%7B1%20-%20e%5E%7B-%5Cboldsymbol%7B%5Cbeta%20I_t%7D%20-%20%5Cboldsymbol%7B%5Clambda_%7Bex%7D%7D%7D%7D_%7B%5Ctext%7Bforce%20of%20infection%7D%7D%29%5Cboldsymbol%7BS_t%7D%20%5Cright%29%7D%5E%7B%5Ctext%7Binfections%7D%7D%20-%5Coverbrace%7B%5Ctext%7BBinom%7D_2%28%5Cboldsymbol%7Bm_S%20S_t%7D%29%7D%5E%7B%5Ctext%7Bmortality%7D%7D%20%5C%5C%0A%5Cboldsymbol%7BI%7D_%7Bt%2B1%7D%20%26%5Csim%20%5Cboldsymbol%7BI_t%7D%20%2B%20%5Ctext%7BBinom%7D_1%5Cleft%28%281%20-%20e%5E%7B-%5Cboldsymbol%7B%5Cbeta%20I_t%7D%20-%20%5Cboldsymbol%7B%5Clambda_%7Bex%7D%7D%7D%29%5Cboldsymbol%7BS_t%7D%20%5Cright%29%20-%20%5Ctext%7BBinom%7D_3%28%5Cboldsymbol%7Bm_I%7D%20%5Cboldsymbol%7BS_t%7D%29%20%0A%5Cend%7Baligned%7D "\begin{aligned} | |
| \boldsymbol{S}_{t+1} &\sim \boldsymbol{S_t} + \overbrace{ \text{Pois}\left[\boldsymbol{b(S_t+I_t)}\left(1-\sum_{i=1}^n w_i (S_{it} + I_{it}) \right) + \boldsymbol{rm_I I_t}\right]}^{\text{new recruits}} - \overbrace{\text{Binom}_1\left((\underbrace{1 - e^{-\boldsymbol{\beta I_t} - \boldsymbol{\lambda_{ex}}}}_{\text{force of infection}})\boldsymbol{S_t} \right)}^{\text{infections}} -\overbrace{\text{Binom}_2(\boldsymbol{m_S S_t})}^{\text{mortality}} \\ | |
| \boldsymbol{I}_{t+1} &\sim \boldsymbol{I_t} + \text{Binom}_1\left((1 - e^{-\boldsymbol{\beta I_t} - \boldsymbol{\lambda_{ex}}})\boldsymbol{S_t} \right) - \text{Binom}_3(\boldsymbol{m_I} \boldsymbol{S_t}) | |
| \end{aligned}") | |
| Here  and  are vectors of the populations of susceptible and infected individuals of each species, and  is the matrix of contact rates. Other parameters are listed below in Table 1. | |
| |Parameter Vector Symbol|Description| | |
| |:----------------------|:----------| | |
| ||Probability of death per year, for both susceptible and infectious trees| | |
| ||Fecundity per individual per year.| | |
| ||Probability of resprouting after death by disease.| | |
| ||Competitive coefficient (relative contribution to density-dependent recruitment)| | |
| ||Rate of contact of each species with pathogen spores from outside the site| | |
| New susceptible trees enter the system via density-dependent seedling recruitment and resprouting from recently killed trees. Susceptible trees become infected at rates proportional contact with infected trees (density-dependent) and pathogen migrating into the system. Both susceptible and infected trees die at constant rates. | |
| The model is modified from Cobb et al. (2012) in several ways: (1) inclusion of demographic stochasticity, (2) conversion from continuous discrete time, (3) the inclusion of , force of infection from areas outside the system, (4) the exclusion of recovery of infected trees, which has not been observed in the field. Finally, the only population structure in Model A is the difference in species parameters. It excludes age structure, and spatial structure, assuming a well-mixed population and frequency-dependent transmission (Following Diekmann et al. (1990)) | |
| The model will be parameterized with three speces: tanoak, bay, and redwood, which will represent all non-host species. And run with initial conditions found in Cobb et al. (2012) and @Filipe2013. | |
| **Model B** adds stage structure to Model A. In this case, the vectors  and  represent the population divided by species and size class: | |
| ![\\begin{aligned} S'\_t &\\sim S\_t - \\text{Binom}\_1\\left((1 - e\^{-\\boldsymbol{\\beta I\_t} - \\boldsymbol{\\lambda\_{ex}}})\\boldsymbol{S\_t} \\right) \\\\ I'\_t &\\sim I\_t + \\text{Binom}\_1\\left((1 - e\^{-\\boldsymbol{\\beta I\_t} - \\boldsymbol{\\lambda\_{ex}}})\\boldsymbol{S\_t} \\right) \\\\ S\_{t+1} &\\sim \\text{Multinom}(\\boldsymbol{A\_S(S'\_t,I'\_t)S'\_t}) + \\text{Pois}\\left[\\boldsymbol{b(S'\_t+I'\_t)}\\left(1-\\sum\_{i=1}\^n w\_i (S'\_{it} + I'\_{it}) \\right) + \\boldsymbol{rm\_I I'\_t}\\right] \\\\ I\_{t+1} &\\sim \\text{Multinom}(\\boldsymbol{A\_I(S'\_t,I'\_t)I'\_t}) \\end{aligned}](http://latex.codecogs.com/gif.latex?%5Cbegin%7Baligned%7D%0AS%27_t%20%26%5Csim%20S_t%20-%20%5Ctext%7BBinom%7D_1%5Cleft%28%281%20-%20e%5E%7B-%5Cboldsymbol%7B%5Cbeta%20I_t%7D%20-%20%5Cboldsymbol%7B%5Clambda_%7Bex%7D%7D%7D%29%5Cboldsymbol%7BS_t%7D%20%5Cright%29%20%5C%5C%0AI%27_t%20%26%5Csim%20I_t%20%2B%20%5Ctext%7BBinom%7D_1%5Cleft%28%281%20-%20e%5E%7B-%5Cboldsymbol%7B%5Cbeta%20I_t%7D%20-%20%5Cboldsymbol%7B%5Clambda_%7Bex%7D%7D%7D%29%5Cboldsymbol%7BS_t%7D%20%5Cright%29%20%5C%5C%0AS_%7Bt%2B1%7D%20%26%5Csim%20%5Ctext%7BMultinom%7D%28%5Cboldsymbol%7BA_S%28S%27_t%2CI%27_t%29S%27_t%7D%29%20%2B%20%5Ctext%7BPois%7D%5Cleft%5B%5Cboldsymbol%7Bb%28S%27_t%2BI%27_t%29%7D%5Cleft%281-%5Csum_%7Bi%3D1%7D%5En%20w_i%20%28S%27_%7Bit%7D%20%2B%20I%27_%7Bit%7D%29%20%5Cright%29%20%2B%20%5Cboldsymbol%7Brm_I%20I%27_t%7D%5Cright%5D%20%5C%5C%0AI_%7Bt%2B1%7D%20%26%5Csim%20%5Ctext%7BMultinom%7D%28%5Cboldsymbol%7BA_I%28S%27_t%2CI%27_t%29I%27_t%7D%29%0A%5Cend%7Baligned%7D "\begin{aligned} | |
| S'_t &\sim S_t - \text{Binom}_1\left((1 - e^{-\boldsymbol{\beta I_t} - \boldsymbol{\lambda_{ex}}})\boldsymbol{S_t} \right) \\ | |
| I'_t &\sim I_t + \text{Binom}_1\left((1 - e^{-\boldsymbol{\beta I_t} - \boldsymbol{\lambda_{ex}}})\boldsymbol{S_t} \right) \\ | |
| S_{t+1} &\sim \text{Multinom}(\boldsymbol{A_S(S'_t,I'_t)S'_t}) + \text{Pois}\left[\boldsymbol{b(S'_t+I'_t)}\left(1-\sum_{i=1}^n w_i (S'_{it} + I'_{it}) \right) + \boldsymbol{rm_I I'_t}\right] \\ | |
| I_{t+1} &\sim \text{Multinom}(\boldsymbol{A_I(S'_t,I'_t)I'_t}) | |
| \end{aligned}") | |
| Here disease transitions are separated in time from demmographic transitions (Klepac and Caswell 2010). In California, *P. Ramorum* reproduces and spreads during the winter rainy season while most tree growth occurs in the spring and fall. | |
| Where  is the matrix of demographic rates specifying transitions between classes and mortality.  is a block-diagonal matrix of size transition matrices, with no transitions between species classes. | |
| **Models 3 and 4** modify Models 1 and 2 by adding spatial structure in the form of a lattice metapopulation.  and  become Individuals do not migrate between sub-populations on the lattice, | |
| - Build series of nested models of varying complexity that incorporate | |
| - Species differences in demographic and epidemiological parameters | |
| - Size structure in demographic and epidemiological parameters | |
| - Spatial structure | |
| - How does inclusion of each component of structure modify | |
| -  (global and local) | |
| - Epidemic size | |
| - Probability of outbreak | |
| - Time to extinction of tanoak and *P. ramorum*. | |
| - Compare models to determine best predictor of disease outbreak | |
| - Determine optimal combination of host- (harvesting) and pathogen-centric (spraying) controls over management periods, given constraints, to minimize probability of disease outbreak | |
| Nested Models | |
| ------------- | |
| - Fit all possible combinations of models: | |
| - Including or excluding size structure of each species (by fixing parameters across classes) | |
| - Including or excluding density dependence on reproduction, growth, and mortality | |
| - Including or excluding disease effects on reproduction, growth, and mortality | |
| - Normal, fat-tailed, or uniform (no spatial structure) dispersal | |
| Table 1: Model Structures | |
| - Mean field | |
| - Mean field with species classification | |
| - Mean field with size classification | |
| - Mean field with species and size classification | |
| - Spatially explicit | |
| - Spaitally explicit with species classification | |
| - SE with size class | |
| - SP with size class and species | |
| Use Klepac and Caswell (2010) structural framework, extended to include multiple species *and* life stages. | |
| - Multinomial draws for transition stochasticity | |
| - Poission distributions for births | |
| - Environmental stochasticity - what does this most effect? | |
| - Spore distribution/creation | |
| Contact Structures | |
| ------------------ | |
| Contact rates in SOD are not driven by differential mixing of groups, but of 3D structure and differing physiological response of the disease. Inter-species studies have mostly focused on (symmetrical) contact structures where within-group contact rates exceed intra-group contact rates, or assymetric contact rates simulating rare jumps between species. | |
| - Observational stochasticity | |
| - Binomial observation probability | |
| - Ask Richard - what do we think false positive and negative rates are like? | |
| Model Fitting and Selection | |
| --------------------------- | |
| In order to determine which model to use for planning and management, I must select from the model structures above by determining which best represents observations from time series data. | |
| Data | |
| ---- | |
| Data to fit the models comes from a collaboration with the Rizzo lab's diease monitoring plot network. The data consist of observations tree size, condition, and disease status from the years 2002-2007. Trees were observed in 14 sites along the California coast from X (36.16°N) to Y (38.35°N), each of which contains X-X 500 m<sup>2</sup>, seperated by minimium distances of Z. All plots are in forests dominated by redwood, tanoak, and Bay Laurel, with negligible other SOD host species. | |
| Size, health, and disease status of all trees were measured in 2002 and 2007, as well as for a random sample of 5 trees of each species in the years 2003-2006. | |
| Each plot within a site will represent one subpopulation within the metapopulation lattice, with the matrix of metapopulations around counting as unobserved. | |
| Model fitting | |
| ------------- | |
| The processes generating the data above may be considered **hidden Markov process** (Gimenez et al. 2012), that is, processes where the state of the system is dependent on its previous state, but where states are partially or imperfectly observed. Each model in Table 1 represents one such process. | |
| In order estimate the hidden Markov process, I require a method to calculate. | |
| **Particle filtering** determines the likelihood of a hidden Markov process by taking advantage of the fact that, at each time step, the likelihood of a system state is dependent on the previous state, and the observation | |
| p(X\_t) = p(X\_t | X\_{t-1}, Y\_t) | |
| The likelihood of the model, given the all of the data, may then be expressed as | |
|  | |
| (Arulampalam et al. 2002) | |
| Since ") is unknown, It's value is determined at each time step by simulation. | |
| PFMCMC requires two components to the model. A **process model** which simulates the states ") of the model, and an **observation model** of the observations at each time point, given underlying states "). Unlike the process model, the observation model must have a tractable likelihood. | |
| For my process model, I will assume that tree presence, size, and location alive/dead status are measured exactly, but that disease status is observed imperfectly via the conditional probabilites | |
|  | |
| p_OS &= p(\text{Observing that tree is healty}|\text{tree is healthy}) | |
| \end{aligned}") | |
| In addition, I assume that the smallest size class is unobserved in models with size classes. | |
| With an estimate of likelihood available, one needs an approach to determine the maximum-likelihood estimate of the model parameters "). Several methods are available. **Iterated filtering** (IF) estimates  by replacing constant parameter values with a random walk  of decreasing variance over time, and determining the "states" of this walk as the variance approaches zero. IF is computationally efficient but requires long time series. | |
| Alternatively, **Particle Filter Markov Chain Monte Carlo** (PFMCMC) uses a Markov Chain sampler (e.g., Metropolis-Hastings), calculating the likelihood at each iteration using a particle filter. While computationally expensive, it does not require long time series and may be used with multiple, independent time series. PFMCMC also integrates particle filtering into a Bayesian context, allowing the use of informative priors. | |
| Model selection | |
| --------------- | |
| Model selection has multiple purposes. First, to determine which model best is most like the true purpose, and to estimate the valdiity of the models for the purposes of prediction. DIC has several advantages. First, it incoporates any random variables. Secondly, it estimates the loss of parameters from Bayesian inference. As several components of the model have useul priors estimated form either data sets, this is useful in this case. | |
| PFMCMC will provide maximum-likelihood parameter estimates and likelihoods for each of the model structures. | |
| In order to compare them, I will use the **deviance information criterion** (Spiegelhalter et al. 2002, DIC), which is defined as | |
|  + 2p_D") | |
| where  is a metric of model complexity (effective number of parameters) and  is the deviance (-2  log likelihood).  defined as | |
| } - D(\bar{\theta})") | |
|  may be redfined as  to correct for the amount of data. | |
| DIC provides a measure of fit and complexity. It has two primary advantages over traditional measures of fit such as BIC and AIC. First, since  is based on the likelihood distribution, it incorporates information from the prior. Effectively, it reduces the effective number of parameters when they are restricted due to the prior. Secondly, the same property allows the effective number of parameters from random variables to be included. | |
| Use of DIC assumes that there is a "best" or "real" model within the comparison. While no models are "true" (Box 1976), this excercise is selecting a "best" or "most useful" model for scenario exploration, rather than predictive model-averaging. | |
| - Compare models via AICc. Eliminate models with AICc weights \< 4x the lowest AICc weight (following Maunder and Deriso (2011)) | |
| Informative priors for disease epidemiological parameters may be determined from previous studies of SOD [@REFS] | |
| Optimization | |
| ------------ | |
| Using the model developed above I will derive optimal control strategies for forest management under the threat of disease outbreak. The basis of this work will be the Hartman (1976) economic modeling framework, in which forest owners are motivated by dual goals of continuous ecosystem service amenities and profit from timber harvest. Under this framework, the optimal control will minimize the costs associated with quarantine and equipment cleaning, while maximizing both the standing biomass of valued species and their timber value. Both time discounting and risk-aversion will be included in the maximization scheme. | |
| Reed (1984) described a forestry model where age-dependent risk of fire modifies the optimal harvest rotation of forest. Fire risk (a nonhomogenous Poisson process) changes through time. | |
| A stochastic implementation of the most parsimonious model will generate a risk of outbreak as a function of forest composition and time. (See Fig 1) | |
| An outline of | |
| - The best-fit model provides us with estimates of the probability over disease outbreaks in a forest stand over a management period. This probability is contingent on both forest composition and spatial structure, and the burden of spores from other areas, and changes over time as forest dynamics change the host population. | |
| By assuming that disease at below-outbreak levels has a negligible effect forest growth, this model can be simplified into a model of disease-free forest dynamics, and an evolving probability of outbreak that changes as a function of forest composition. | |
| By considering probability of disease outbreak a nonhomogenous poisson process, we may use the Reed (1984) framework and extensions to calculate optimal control techniques. | |
| This becomes n optimal control problem in which  is the annual cost of reducing the probability of disease arrival , and  is the cost of silvicultural treatment in any year of cutting. | |
| The goal will be to solve the dynamic optimization. | |
| Probability of outbreak will be reduced with lower populations of trees. | |
| Contraints: | |
| Budget (both annual and total scenarios) --\> Minimize outbreak probability Maximum probability of outbreak --\> Minimize cost | |
| - Both composition and the arrival of disease can be modified by controls. Select cutting may modify the composition and managment actions such as the cleaning of logging equipment can reduce the arrival of spores. Pesticides can also reduce the probability of spores successfully infecting healthy trees. All of these management actions (including logging) have costs, and are limited by budget constraints of management agencies and/or landowners | |
| - The solution to this optimal control problem will be an optimal *treatment rotation* - a schedule of harvest and spraying actions that minimize risk over the treatment period. | |
| - An alternative useful formulation of the problem is to determine the minimum-cost method given constraints of desired tree population and *maximum acceptable probability of outbreak*. An advantage of this approach is to provide managers with an method of implicit valuation of the tanoak population by illustrating the trade-off between costs and acceptable tree populations and risks. | |
| - Examine under a variety of regulatory constraints: limiting herbicide use for suppressing sprounts and others, harvest regulations in riparian areas, endangered species limitation on time/space of cutting. | |
| - An extension of the analysis above will include the parameter uncertainty of the best-fit model, and an optimization under the scenario that parameter uncertainties decrease with time | |
| * * * * * | |
| Optimization | |
| ============ | |
| The best-fit model that captures essential aspects of the disease dynamics will be used to develop an optimal control solution to minimization of disease risk over time. | |
| In this, modeled after the XXXX area outbreak, goals for SOD forest management can be approximated as (a) maintaining a minimum density of at-risk species (i.e., tanoak), and (b) minimizing the probability of outbreak. | |
| Tools for SOD control can be categorized into two types. Silvicultural (“host-centric”) treatments change forest composition. “Pathogen-centric” treatments, such as quarantine, equipment cleaning and spraying, reduce the probability of spore arrival. | |
| Cutting events are discrete, periodic treatments that change forest composition. A cut can reduce the density of any class and species to either the levels associated with minimum probability of outbreak, or to minimum socially acceptable densities. Tanoak and bay laurel trees have little timber value (@REF), so each cut has a one-time cost, . For the purpose of this model  is independent of the extent of density reduction. | |
|  represents the combined annual costs of measures to reduce the external force of infection . | |
| This model could be optimized by defining a function for the value of ecosystem services flowing annually from the forest annually as a function of the forest composition ") [@Hartmann1976]. However, due to the difficulty of defining and valuing these services, it is more feasible to define constraints that represent the range of socially acceptable outcomes. | |
| The constraint that makes most sense is a *minimum acceeptable density of the species of interest* "). This value could be further specified to include, for instance, a minimum density of trees of a minimum size. Since the system is stochastic, this constraint expressed by a *level of acceptable risk*, the probability that the species density will fall beneath this value "). | |
| The dynamic optimization problem is to minimize the cost of treatment while maintaining the outbreak probability below : | |
|  \text{ s.t. } p(N_t < N_{\min}) < p_{text{acc}}") | |
| An alternative formulation, also useful to managers, is to minimize the probability of outbreak given budget constraints. Budget constraints could be forumulated as total budgets for the entire mangement period, or annual limits on spending. | |
|  \leq B_T") | |
| or | |
|  \leq B_{\text{ann}} \forall T") | |
| References | |
| ========== | |
| Anderson, R. M., and R. M. May. 1985. Age-related changes in the rate of disease transmission: implications for the design of vaccination programmes. J. Hyg. Camb. | |
| Arulampalam, M. S., S. Maskell, N. Gordon, and T. Clapp. 2002. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Transactions on Signal Processing 50:174–188. | |
| Box, G. E. P. 1976. Science and Statistics. Journal of the American Statistical Association 71:791–799. | |
| Brown, D. H., and B. M. Bolker. 2004. The effects of disease dispersal and host clustering on the epidemic threshold in plants. Bulletin of mathematical biology 66:341–71. | |
| Cobb, R. C., J. A. N. Filipe, R. K. Meentemeyer, C. A. Gilligan, and D. M. Rizzo. 2012. Ecosystem transformation by emerging infectious disease: loss of large tanoak from California forests. Journal of Ecology:no–no. | |
| Craft, M. E., and P. L. Hawthorne. 2008. Dynamics of a multihost pathogen in a carnivore community. Journal of Animal Ecology 77:1257–1264. | |
| Davidson, J. M., A. C. Wickland, H. A. Patterson, K. R. Falk, and D. M. Rizzo. 2005. Transmission of Phytophthora ramorum in Mixed-Evergreen Forest in California. Phytopathology 95:587–596. | |
| DiLeo, M. V., R. M. Bostock, and D. M. Rizzo. 2009. Phytophthora ramorum does not cause physiologically significant systemic injury to California bay laurel, its primary reservoir host.. Phytopathology 99:1307–11. | |
| Diekmann, O., J. A. P. Heesterbeek, and J. A. J. Metz. 1990. On the definition and the computation of the basic reproduction ratio R 0 in models for infectious diseases in heterogeneous populations. Journal of Mathematical Biology 28:365–382. | |
| Dobson, A. 2004. Population dynamics of pathogens with multiple host species.. The American Naturalist 164 Suppl:S64–78. | |
| Filipe, J. A. N., and M. M. Maule. 2003. Analytical methods for predicting the behaviour of population models with general spatial interactions. Mathematical Biosciences 183:15–35. | |
| Filipe, J. A. N., and M. M. Maule. 2004. Effects of dispersal mechanisms on spatio-temporal development of epidemics. Journal of Theoretical Biology 226:125–141. | |
| Gilbert, G. S., and S. P. Hubbell. 1996. Diseases and the Tropical of Conservation Forests. BioScience 46:98–106. | |
| Gimenez, O., J. D. Lebreton, J. M. Gaillard, R. Choquet, and R. Pradel. 2012. Estimating demographic parameters using hidden process dynamic models. Theoretical Population Biology 82:307–316. | |
| Hansen, E. M., and E. M. Goheen. 2000. Phellinus Weirii and other Native Root Pathogens as Determinants of Forest Structure and Process in Western North America. Annual review of phytopathology 38:515–539. | |
| Hartman, R. 1976. The Harvesting Decision when a Standing Forest has Value. Economic Inquiry 14:52–58. | |
| Holdenrieder, O., M. Pautasso, P. J. Weisberg, and D. Lonsdale. 2004. Tree diseases and landscape processes: the challenge of landscape pathology.. Trends in ecology & evolution (Personal edition) 19:446–52. | |
| Ionides, E. L., C. Bretó, and a a King. 2006. Inference for nonlinear dynamical systems. Proceedings of the National Academy of Sciences of the United States of America 103:18438–43. | |
| Kermack, W. O., and A. G. Mckendrick. 1927. A Contribution to the Mathematical Theory of Epidemics. Proceedings of the Royal Society of London. Series A: Mathematical and Physical Sciences 115:700–721. | |
| Klepac, P., and H. Caswell. 2010. The stage-structured epidemic: linking disease and demography with a multi-state matrix approach model. Theoretical Ecology 4:301–319. | |
| Knape, J., and P. de Valpine. 2012. Fitting complex population models by combining particle filters with Markov chain Monte Carlo.. Ecology 93:256–63. | |
| Kovacs, K., T. Václavík, R. G. Haight, A. Pang, N. J. Cunniffe, C. a Gilligan, and R. K. Meentemeyer. 2011. Predicting the economic costs and property value losses attributed to sudden oak death damage in California (2010-2020).. Journal of environmental management 92:1292–302. | |
| Lovett, G. M., C. D. Canham, M. A. Arthur, C. Kathleen, R. D. Fitzhugh, and K. C. Weathers. 2006. Forest Ecosystem Responses to Exotic Pests and Pathogens in Eastern North America. BioScience 56:395–405. | |
| Maunder, M. N., and R. B. Deriso. 2011. A state – space multistage life cycle model to evaluate population impacts in the presence of density dependence : illustrated with application to delta smelt ( Hyposmesus transpacificus ). Canadian Journal of Fisheries and Aquatic Science 1306:1285–1306. | |
| Meentemeyer, R. K., N. J. Cunniffe, A. R. Cook, J. A. N. Filipe, R. D. Hunter, D. M. Rizzo, and C. a Gilligan. 2011. Epidemiological modeling of invasion in heterogeneous landscapes: spread of sudden oak death in California (1990–2030). Ecosphere 2:1–24. | |
| Metcalf, C. J. E., J. Lessler, P. Klepac, A. Morice, B. T. Grenfell, and O. N. Bjø rnstad. 2012. Structured models of infectious disease: Inference with discrete data. Theoretical population biology 82:275–282. | |
| Metz, M. R., K. M. Frangioso, A. C. Wickland, R. K. Meentemeyer, and D. M. Rizzo. 2012. An emergent disease causes directional changes in forest species composition in coastal California. Ecosphere 3:art86. | |
| Park, A. W., S. Gubbins, and C. A. Gilligan. 2002. Extinction times for closed epidemics: the effects of host spatial structure. Ecology Letters 5:747–755. | |
| Park, A. W., S. Gubbins, and C. a Gilligan. 2001. Invasion and persistence of plant parasites in a spatially structured host population. Oikos 94:162–174. | |
| Reed, W. J. 1984. The effects of the risk of fire on the optimal rotation of a forest. Journal of Environmental Economics and Management 11:180–190. | |
| Rizzo, D. M., M. Garbelotto, J. M. Davidson, G. W. Slaughter, and S. T. Koike. 2002. Phytophthora ramorum and sudden oak death in California: I. Host relationships. Pages 733–740 *in* Fifth Symposium on Oak Woodlands: Oaks in California’s Changing Landscapes. . USDA Forest Service, San Diego, CA. | |
| Rizzo, D. M., M. Garbelotto, and E. M. Hansen. 2005. Phytophthora ramorum: integrative research and management of an emerging pathogen in California and Oregon forests. Annual review of phytopathology 43:309–35. | |
| Rizzo, D. M., and M. Garbelotto. 2003. Sudden oak death: endangering California and Oregon forest ecosystems. Frontiers in Ecology and the Environment 1:197–204. | |
| Spiegelhalter, D. J., N. G. Best, B. P. Carlin, and A. van der Linde. 2002. Bayesian measures of model complexity and fit. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 64:583–639. | |
| Swiecki, T. J., and E. Bernhardt. 2005. Disease risk factors and disease progress in coast live oak and tanoak affected by Phytophthora ramorum canker (sudden oak death). Pages 383–411 *in* Proceedings of Sudden Oak Death Science Symposium II. PJ Shea and M. Haverty, eds. Pacific Southwest Research Station, Forest Service, US Department of Agriculture, Albany, CA. | |
| Swiecki, T. J., and E. A. Bernhardt. 2013. Managing sudden oak death in California: before, during, and after Phytophthora ramorum invasion. . U.S. Department of Agriculture; Forest Service; Pacific Southwest Research Station. | |
| Vehtari, A., and J. Ojanen. 2012. A survey of Bayesian predictive methods for model assessment, selection and comparison. Statistics Surveys 6:142–228. |
Sign up for free
to join this conversation on GitHub.
Already have an account?
Sign in to comment