Consider the need to use a dictionary. You will have to insert , look-up , remove words to and from it. What data structure would you use ? Would you use a hash table ? Would that be efficient in terms of memory? Perhaps not.
A Trie is a tree like data structure used for storing words in a way which facilitates fast look-ups. They prove very useful for handling dictionaries. What is special about them is that you can determine the longest common prefix between multiple words and even use it for autocompletion of words.
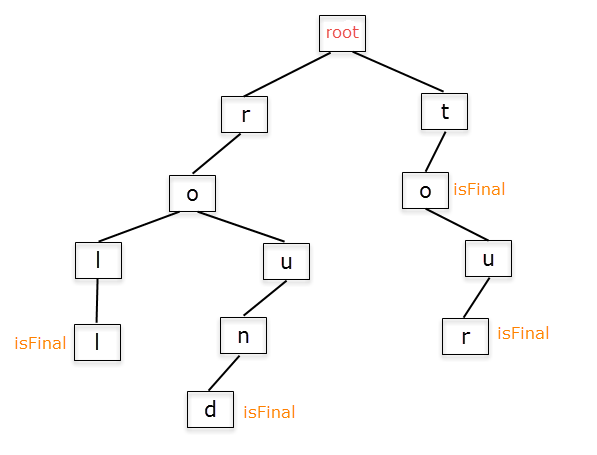
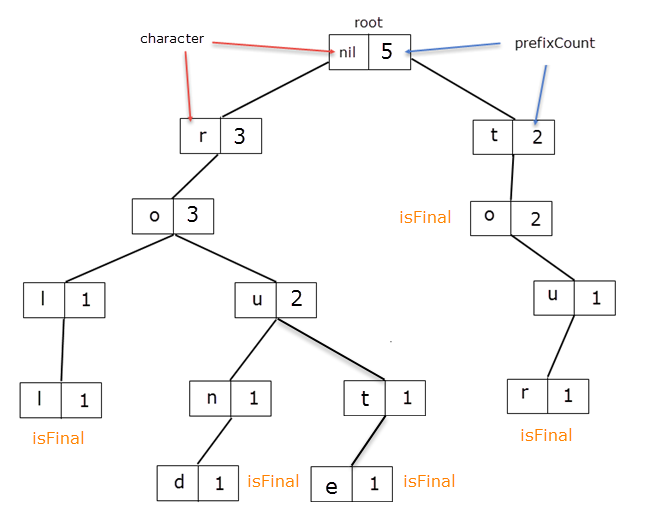
The concept behind tries is easy to understand and to implement. Suppose you have 4 words: roll, round, to, tour. Here is how their corresponding Trie looks:
This article will walk you through a series of 14 steps. Completing them will gurantee you a basic understanding of tries. #####1. Tree Data Structure #####2. Example of a Trie #####3. TrieNode and Trie Classes #####4. Insert #####5. Query #####6. Remove #####7. Prefix Counter #####8. Unique Words #####9. Words Same Prefix #####10. Remove Words Same Prefix #####11. kth Word #####12. Validate Character Sequence #####13. Generics #####14. Suggestions and Auto-Completion
Tree data structures are inspired from nature. A tree data structure has a root, branches, and leaves. The difference between a tree in nature and a tree in computer science is that a tree data structure has its root at the top and its leaves on the bottom.
Take the folder hierarchy for example:

root - starting point of the Tree
edge - the connection between one node and another
child - node directly connected to another node when going one level down
parent - converse notion of a child
leaf - node with no children
path - A sequence of nodes and edges connecting a node with a descendant.
To begin with, let's represent a Trie containing lowercase words. Each TrieNode will have a lowercase character bound to it (except the root Node) and a limited number of children, given by the length of the alphabet (the english alphabet has 26 letters) .
The following is a representation of a Trie containing the words : round, roll, to, tour.
isFinal indicates whether a TrieNode corresponds to the last character of a word.
Notice that the words "roll" and "round" have the "ro" prefix in common, while the words "to" and "tour" have in common "to".
Enough with the theory, let's start coding !
class TrieNode {
var children: [Character:TrieNode] = [:]
var isFinal: Bool = false
init() {
}
//...
}children bounds characters to children TrieNodes.
The Trie class will have only one stored member. Guess which one :)
class Trie {
var root = TrieNode()
//...
}Inserting means creating new TrieNodes and that functionality should be provided by the TrieNode class. Therefore, we need to add more functions to it .
//...
func createChildFor(_ character: Character) -> TrieNode {
let node = TrieNode()
children[character] = node
return node
}
func getOrCreateChildFor(_ character: Character) -> TrieNode {
if let child = children[character] {
return child
} else {
return createChildFor(character)
}
}They are used for finding or creating the TrieNode corresponding to character and then return it.
Now we can proceed to adding our first few words to the Trie.
Given a String, we iterate it character by character. Starting from the root, we use getOrCreateChildFor(character) and switch to the newly created node.
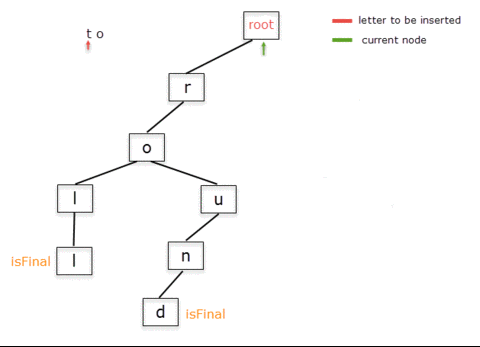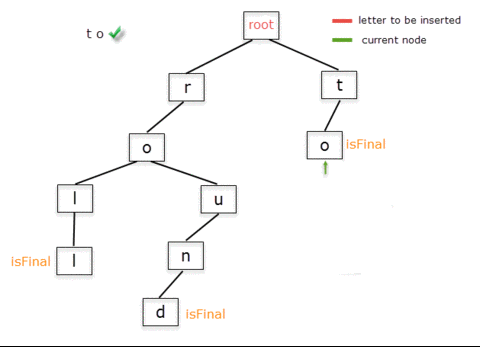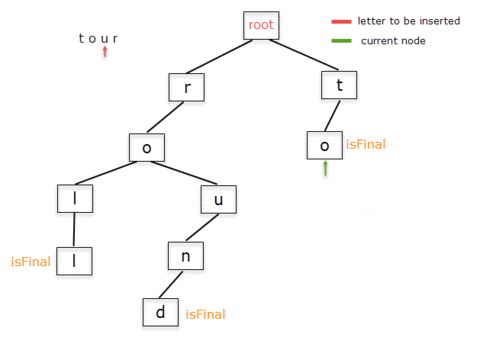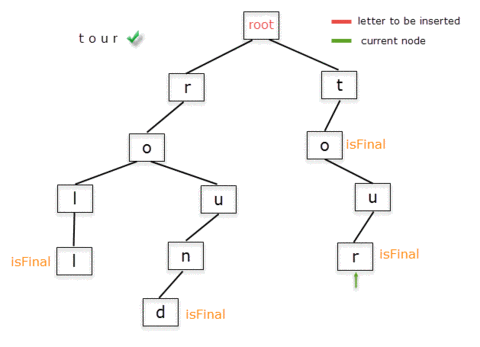
Below is the step-by-step representation of adding the words "roll" and "round".
Notice that in the process of inserting "roll" we create nodes for all characters in the word, while for adding "round" we don't create additional nodes for the already existing prefix "ro". We only insert the nodes for "und".
Inserting the words "to" and "tour" will follow the same procedure. Inserting "to" means creating a child with letter "t" from the root node and, from it, another for the letter "o". Now, when inserting "tour", "to" is part of the Trie, so we only need to insert "ur".
Here's a straightforward implementation using the helper functions from the TrieNode class.
func insert(_ word: String){
insert(characters: Array(word.characters))
}
func insert(characters: [Character]) {
var node = root
for character in characters {
node = node.getOrCreateChildFor(character)
}
node.isFinal = true //
}The function should return true if a given word is present in the Trie, false otherwise.
Remark: our Trie contains only unique words
The process is very similar to the Insert function. Instead of creating a node at each step, we only check for its existence. When we get to the last character of the word, the corresponding TrieNode must have isFinal set to true, in order for the query to return true.
func query(_ word: String) -> Bool {
return query(characters: Array(word.characters))
}
func query(characters: [Character]) -> Bool {
var node : TrieNode? = root
for character in characters {
node = node?.children[character]
if node == nil {
return false
}
}
return node!.isFinal
}This line of code is something called Optional Chaining and it lets us write cleaner code.
node = node?.children[character]When it encounters the first nil in the expression it automatically returns nil.
Remove works the same way query does, but we change isFinal at the last TrieNode.
func remove(_ word: String){
remove(characters: Array(word.characters))
}
func remove(characters: [Character]) {
var node : TrieNode? = root
for character in characters {
node = node?.children[character]
if node == nil {
return
}
}
node!.isFinal = false
}What do you notice with this implementation ?
If we delete the word "round", this is how the Trie will look like:
We are still left with the actual sequence "round" in the Trie, but the next queries will return false because isFinal would be set to false, when called for the word "round".
The following code :
var myTrie = Trie()
myTrie.insert("roll")
myTrie.insert("round")
print(myTrie.query("round"))
myTrie.remove("round")
print(myTrie.query("round"))will print: true false
If we were to remove the actual sequence, we would have to delete the TrieNode references from the children member, the key - value pairs, for each node in the Trie.
It would be useful to have the path in TrieNodes for a given word, don't you think ?
func getNodeSequence(characters: [Character]) -> [(Character, TrieNode)] {
var node : TrieNode? = root
var nodes:[(Character,TrieNode)] = []
var tup = (Character("@"),node!) // just a random character
// it's not going to be used
nodes.append(tup)
for character in characters {
node = node?.children[character]
if node == nil {
return nodes
}
var tup = (character, node!)
nodes.append(tup)
}
return nodes
}The idea is to iterate backwards the sequence returned by the previous function. At each step we check for the node to have isFinalset to true or to have at least one child. If none of these requirements is met, the node reference is deleted from the Trie.
Because of deleting the word "round", we have our first TrieNode pointing to the "d" letter. None of the previous mentioned requirements are met, so the reference to this node is going to be deleted from the TrieNode.children corresponding to the letter "n".
Here's a step by step explanation for the new remove function:
Also for the the word "roll":
with the corresponding implementation:
func remove2(characters: [Character]) {
var nodes:[(Character,TrieNode)] = getNodeSequence(characters: characters)
if nodes.count != characters.count + 1 {
return
}
nodes[nodes.count - 1].1.isFinal = false
for i in (1..<nodes.count).reversed() {
if nodes[i].1.isFinal {
break
}
if nodes[i].1.children.count >= 1{
break
}
nodes[i - 1].1.children.removeValue(forKey: nodes[i].0)
// we delete the reference from the parent node
// and because that was the only reference to that Trieode in our program
// the TrieNode will be erased from memoery
}
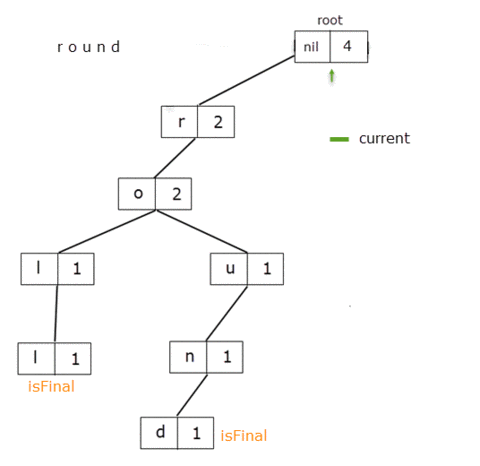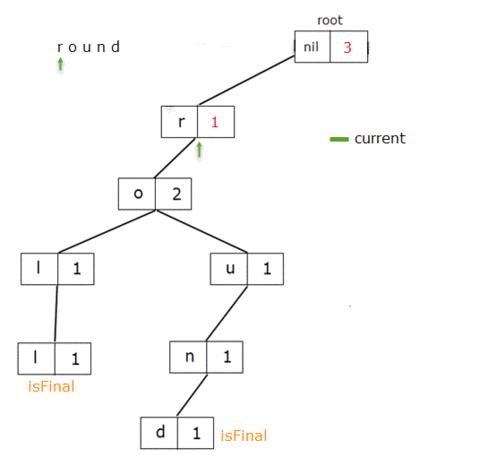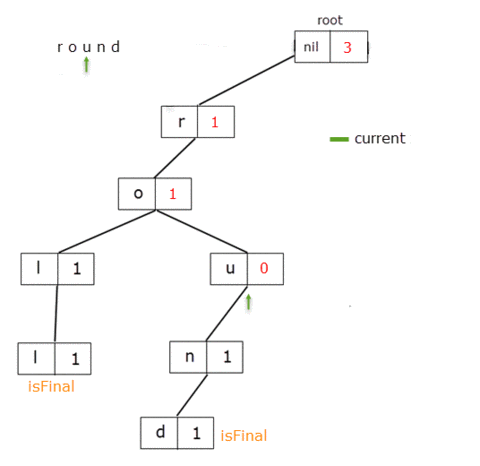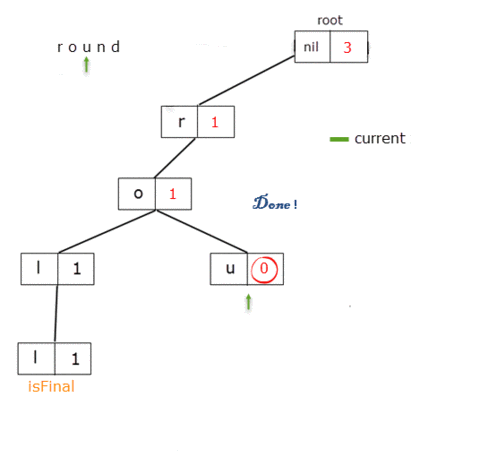
}Having the isFinal member helps, but it doesn't offer enough functionalities. If we were to count the number of unique words in our dictionary, how would you do it ?
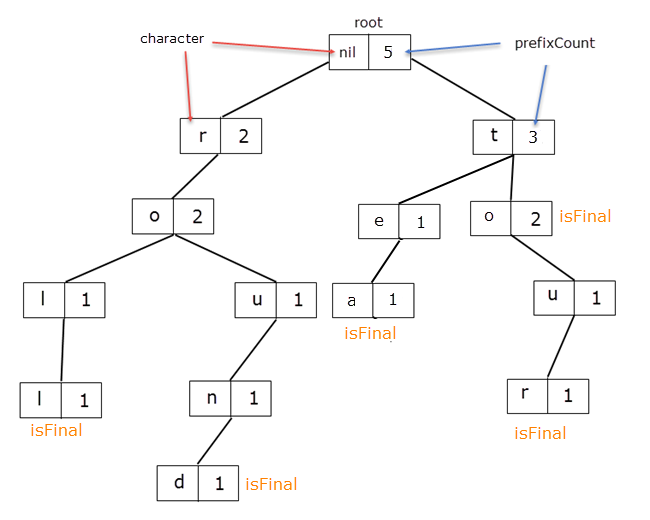
A short answer : a new TrieNode member calledprefixCount.
class TrieNode{
var children: [Character:TrieNode] = [:]
var isFinal: Bool = false
var prefixCount: Int = 0
init() {
}
//...
According to the previous graphical representation, the insertand remove functions suffer changes.
When inserting a word, a simple rule would be to increment prefixCount for each node of the way, including the root.
And the implementation doesn't change much:
func insert(_ word: String){
insert(characters: Array(word.characters))
}
func insert(characters: [Character]) {
var node = root
node.prefixCount += 1
for character in characters {
node = node.getOrCreateChildFor(character)
node.prefixCount += 1
}
node.isFinal = true //
}The query function doesn't need modifications, but that's not the case for remove.
Having the sequence of nodes for a word given by getNodeSequence, we need to decrement the prefixCount value for each node. After we do that, we also do the check prefixCount == 0. If it's true, it means that there are no words in our dictionary that reach that node. It's safe to remove the entire sequence of nodes from now on.
Step by step:
func remove(_ word: String){
remove(characters: Array(word.characters))
}
func remove(characters: [Character]) {
var charactersNodes:[(Character,TrieNode)] = getNodeSequence(characters: characters)
if charactersNodes.count != characters.count + 1 {
return
}
for i in 0..<charactersNodes.count {
charactersNodes[i].1.prefixCount -= 1
if charactersNodes[i].1.prefixCount == 0 {
if i != 0 {
charactersNodes[i - 1].1.children.removeValue(forKey: charactersNodes[i].0)
return // we completely deleted the reference to an entire sequence of nodes
// swift will delete those nodes from memory
}
}
}
charactersNodes[charactersNodes.count - 1].1.isFinal = false
}Mentioned in the previous chapter, the implementation consists in returning the prefixCount member of the root node. How simple is that ? :)
func uniqueWords() -> Int {
return root.prefixCount
}Given a prefix, the function returns how many words in our dictionary have it in common. Take the Trie from chapter 7. If we were to call the function for the prefixes "t", "to", the function would return 2 because both "to" and "tour" share those prefixes. Same logic goes for "r", "ro".
Every word is a prefix of it's own; therefore, calling the function with one of the 4 words in our dictionary( roll, round, to, tour) will return 1. 1 is also returned when called for the prefix "roun" for example.
Here's how we do it:
We iterate the word character by character. If the corresponding TrieNode doesn't exist, we return 0; otherwise we return the value of prefixCount from the last TrieNode.
func wordsSamePrefix(_ word: String) -> Int {
return wordsSamePrefix(characters: Array(word.characters))
}
func wordsSamePrefix(characters: [Character]) -> Int {
var node : TrieNode? = root
for character in characters {
node = node?.children[character]
if node == nil {
return 0
}
}
return node!.prefixCount
}Notice how similiar the function is to query. They both use the last TrieNode of the sequence. In order to avoid repeating code, we might just create a function to return that node, if it exists.
func getNodeFor(_ characters: [Character]) -> TrieNode?
var node: TrieNode? = root
for character in characters {
node = node?.children[character]
}
return node
}And the query and wordsSamePrefix functions will look cleaner:
func query(_ word: String) -> Bool {
return query2(characters: Array(word.characters))
}
func query2(characters: [Character]) -> Bool {
let node = getNodeFor(characters)
if node == nil {
return false
}
return node!.isFinal
}
func wordsSamePrefix(_ word: String) -> Int {
return wordsSamePrefix(characters: Array(word.characters))
}
func wordsSamePrefix(characters: [Character]) -> Int {
let node = getNodeFor(characters)
if node == nil {
return 0
}
return node!.prefixCount
}The function will remove all words having some prefix. The only diference from this and the remove function is that we decrease the prefixCountmember of all TrieNodes with the prefixCount of the last character TrieNode.
To make the example clear, consider adding to our previous Trie the word tea aswell.
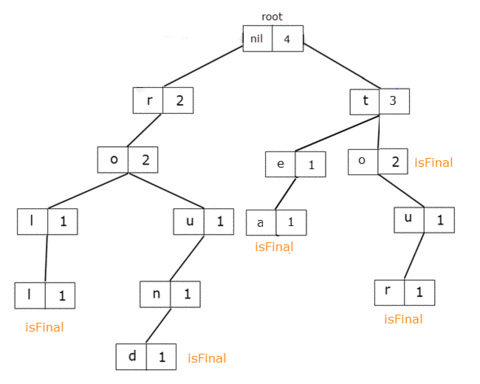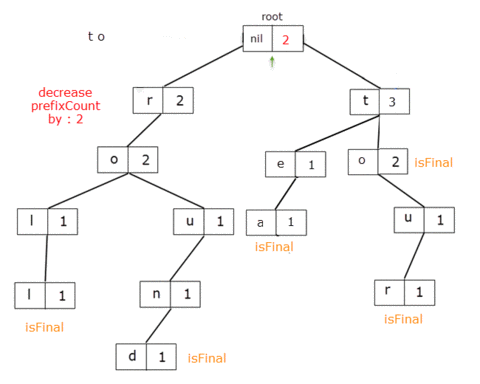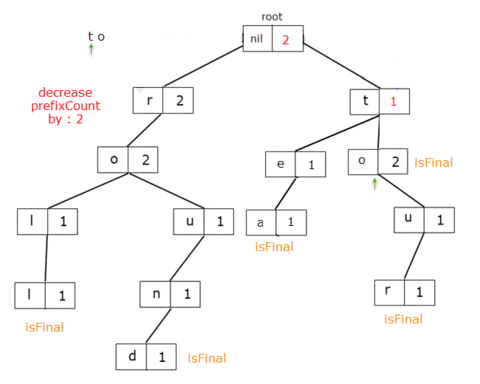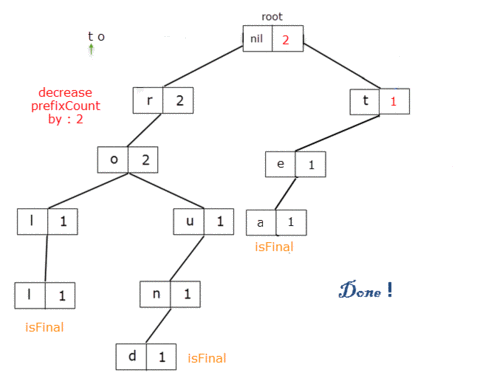
Now, let's say I want to remove all the words with the prefix "to". That means a total of 2 words: to, tour.
When we get to the TrieNode for the letter 'o', we delete the reference from 't' to it. For root, prefixCount = 5and for the letter 't', prefixCount = 3 which, should in fact be 3 and 1 respectively.
It means that for these TrieNodes the prefixCount member should be decreased by 2, the value from the letter 'o'.
Returns the k-th word in our dictionary (k>=0 && k < uniqueWords).
Bellow is a recursive implementation which should be called with one parameter:atIndex(the k value previously mentioned).
func kthword(atIndex index: Int, from node: TrieNode? = nil, characters: [Character] = []) -> String? {
let node = node ?? root
if index >= self.uniqueWords() {
return nil
}
var alphabetString = "abcdefghijklmnopqrstuvxyz"
var alphabetSequence = Array(alphabetString.characters)
if index == 0 && node.isFinal {
return String(characters)
}
var skipped = 0
if node.isFinal {
skipped += 1
}
for char in alphabetSequence {
if let child = node.children[char] {
if skipped + child.prefixCount > index {
// find the word in the current child
return kthword(atIndex: index - skipped, from: child, characters: characters + [char])
} else {
// skip words
skipped += child.prefixCount
}
}
}
return nil
}The line let node = node ?? root uses something called nil- coalescing. Directly from apple developer:
The nil-coalescing operator (a ?? b) unwraps an optional a if it contains a value, or returns a default value b if a is nil. The expression a is always of an optional type. The expression b must match the type that is stored inside a.
Based on the index of the sequence to be followed from that node, we call the function recursively with the proper child and indexas follows:
We iterate through its children. If a child's prefixCount is less or equal than our index value, we add it to skipped, which indicates how many words we are skipping with that child.
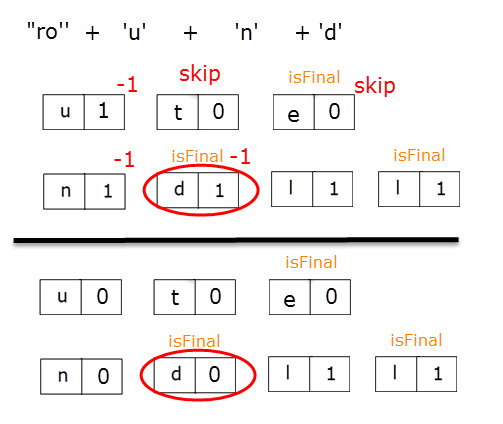
When we get to a node and skipped + child.prefixCount > index it means that our kth word is within that child's reach and we call the function recursively with that child and index = index - skipped. The index is adjusted so that we refer to the sequences starting form that child.
Our goal is to find a node with index == 0 && node.isFinal.
It may not look so efficient to iterate the entire alphabet at each step(for char in alphabetSequence{ }), but it's either that or sorting the dictionary keys:
Bellow is a representation of kthWord(atIndex: 2):
and kthWord(atIndex: 4)
So far, we've assumed that all our input data was valid. We've assumed that all Strings given as parameters for querry,insert, etc. contained lowercase english characters, but what if they didn't ?
The only solution is to check that all Characters in the sequence belong to the given alphabet, one by one...
func validate(characters: [Character]) -> Bool {
var alphabetString = "abcdefghijklmnopqrstuvxyz"
var alphabetSequence = Array(alphabetString.characters)
return characters.reduce(true) { result, char in
return result && alphabetSequence.contains(char)
}
}We use validate as a precondition, indicated by guard:
func insert(_ word: String){
insert(characters: Array(word.characters))
}
func insert(characters: [Character]) {
guard validate(characters: characters) else {
return
}
//...
}
func query(_ word: String) -> Bool {
return query(characters: Array(word.characters))
}
func query(characters: [Character]) -> Bool {
guard validate(characters: characters) else {
return false
}
//...
}
func remove(_ word: String){
remove(characters: Array(word.characters))
}
func remove(characters: [Character]) {
guard validate(characters: characters) else {
return
}
//...Run example:
let myTrie = Trie()
myTrie.insert("to");
myTrie.insert("tO"); // it won't insert the word, because "O" is UPPERCASE
print(myTrie.query("tO")) // false
print(myTrie.query("to")) // true
The complete code for the lowercase alphabet can be found here : http://pastebin.com/dmPdzzkj
We used so far the lowercase english alphabet for our Trie. It's time to generalize the Alphabet.
protocol Alphabet {
associatedtype AlphabetCharacter: Comparable, Hashable
func allCharacters() -> [AlphabetCharacter]
}The AlphabetCharacter needs to be Comparable for the kthWord function and Hashable because it will be used as a key in a dictionary.
lowercase english alphabet:
class LowercaseLetters: Alphabet {
typealias AlphabetCharacter = Character
func allCharacters() -> [AlphabetCharacter] {
return Array("abcdefghijklmnopqrstuvwxyz".characters)
}
required init() {
}
}Bellow is the TrieNode for a generic T which respects the Alphabet protocol:
class TrieNode<T> where T:Alphabet {
typealias character = T.AlphabetCharacter
var children: [character:TrieNode<T>] = [:]
var prefixCount: Int = 0
var isFinal:Bool = false
init() {
}
func createChildFor(_ character: character) -> TrieNode<T> {
let node = TrieNode<T>()
children[character] = node
return node
}
func getOrCreateChildFor(_ character: character) -> TrieNode<T> {
if let child = children[character] {
return child
} else {
return createChildFor(character)
}
}
}All Trie functionalities stay the same:
class Trie<T> where T:Alphabet {
typealias character = T.AlphabetCharacter
typealias Node = TrieNode<T>
var root = Node()
func validate(characters: [character]) -> Bool {
let allCharacters = T().allCharacters()
return characters.reduce(true) { result, char in
return result && allCharacters.contains(char)
}
}
func insert<U:CharacterSequence>(_ word: U) where U.SequenceCharacter == character {
insert(characters: word.toSequence())
}
func insert(characters: [character]) {
guard validate(characters: characters) else {
return
}
var node = root
node.prefixCount += 1
for character in characters {
node = node.getOrCreateChildFor(character)
node.prefixCount += 1
}
node.isFinal = true //
}
//.....
Notice that the new insert function takes a generic U which conforms to the protocol CharacterSequence:
protocol CharacterSequence {
associatedtype SequenceCharacter: Comparable, Hashable
func toSequence() -> [SequenceCharacter]
init(characters: [SequenceCharacter])
}The reasons for making the SequenceCharacter conform to Comparable and Hashable are the same as for the alphabet.
The syntax where U.SequenceCharacter == character is a generic type check, which makes sure that SequenceCharacter == AlphabetCharacter.
All our non-generic functions took a String as parameter and we would call the functions with a Character array. To be able to use String that way with generics, we need to conform it to our protocol:
extension String: CharacterSequence {
typealias SequenceCharacter = Character
func toSequence() -> [SequenceCharacter] {
return Array(characters)
}
init(characters: [SequenceCharacter]) {
self.init(characters)
}
}The need of the constructor is caused by the following non-generic syntax of the kthWord function: return String(characters).
This is how the new function looks like :
func kthword<U:CharacterSequence>(atIndex index: Int, from node: Node? = nil, characters: [character] = []) -> U? where U.SequenceCharacter == character {
let node = node ?? root
if index == 0 && node.isFinal {
return U(characters: characters)
}
var skipped = 0
if node.isFinal {
skipped += 1
}
for char in T().allCharacters() {
if let child = node.children[char] {
if skipped + child.prefixCount > index {
// find the word in the current child
return kthword(atIndex: index - skipped, from: child, characters: characters + [char])
} else {
// skip words
skipped += child.prefixCount
}
}
}
return nil
}Test Run:
let myTrie = Trie<LowercaseLetters>()
myTrie.insert("to");
myTrie.insert("tour");
myTrie.insert("tea");
myTrie.insert("roll");
myTrie.insert("round");
myTrie.remove("roLl")
print (myTrie.query("roll")) // true
myTrie.removeWordsPrefix("r")
print (myTrie.query("roll")) // false
print(myTrie.wordsSamePrefix("t")) // 3
// current words in our dictionary :tea, to, tour
let word: String = myTrie.kthWord(atIndex: 2)!
print(word) // tourThe complete code can be found at: http://pastebin.com/Tm57evsn
How about having a Trie for Integers. Instead of a String, we will have Int and the alphabet will consist of all digits from 0...9. How hard can that be to implement ?
class DigitsAlphabet: Alphabet {
typealias AlphabetCharacter = Int8
func allCharacters() -> [AlphabetCharacter] {
return Array(0...9)
}
required init() {
}
}extension Int: CharacterSequence {
typealias SequenceCharacter = Int8
func toSequence() -> [SequenceCharacter] {
return String(self).characters.map { character in
let asString = "\(character)"
let asInt = Int(asString)!
let asInt8 = Int8(asInt)
return asInt8
}
}
init(characters: [SequenceCharacter]) {
var value = 0
var p = 1
for char in characters.reversed() {
value += p * Int(char)
p *= 10
}
self.init(value)
}
}The constructor takes an array of Int8 and makes an Int out of it, while the toSequence()does the opposite by using a clerver mapping:
the Int is converted to an String then each Character is mapped to an Int8.
Test Run:
let myTrie2 = Trie<DigitsAlphabet>()
myTrie2.insert(12);
myTrie2.insert(123);
myTrie2.insert(13);
myTrie2.insert(133);
myTrie2.insert(134);
myTrie2.insert(211);
myTrie2.remove(12)
print(myTrie2.query(12)) // false
print(myTrie2.query(123)) // true
myTrie2.removeWordsPrefix(12)
print(myTrie2.query(123)) // false
print(myTrie2.wordsSamePrefix(13)) // 3 // 13, 133, 134When you are typing something and a list of words appear, it's our Trie in play!
The function will take a CharacterSequence as prefix and will return [CharacterSequence] containing the suggested words.
func suggestWords<U:CharacterSequence>(_ word: U) -> [U] where U.SequenceCharacter == character {
return suggestWords(characters: word.toSequence())
}
func suggestWords<U:CharacterSequence>(characters: [character]) -> [U] where U.SequenceCharacter == character{
guard validate(characters: characters) else {
return []
}
let lastNodeCharacters = getNodeFor(characters: characters)
if lastNodeCharacters == nil {
return []
//... to be continued
}If given "prefix" is not contained in the Trie, we will return an empty list.
Otherwise, using a DFS, we get all nodes accessible from the prefix.
We need them as tuples of the following form (node, corresponding character, prefixCount).
PrefixCount will dictate how to compute words.
Bellow is a standard DFS.
func DFS(node: Node, char: character ) -> [(node: Node, char: character, counter: Int)] {
let allCharacters = T().allCharacters()
var discoveredNodes:[(node: Node, char: character, counter: Int)] = []
var stackOfNodes = Stack<(node: Node,char: character, counter: Int)>()
stackOfNodes.push((node: node, char: char, counter: node.prefixCount ))
var nodeChar:(node: Node, char: character, counter: Int)
while !stackOfNodes.isEmpty(){
nodeChar = stackOfNodes.pop()
discoveredNodes.append(nodeChar)
for character in allCharacters {
if let inter = nodeChar.node.children[character] {
stackOfNodes.push((node:inter, char:character, counter:inter.prefixCount))
}
}
}
return discoveredNodes
}Our main function will look like this:
func suggestWords<U:CharacterSequence>(characters: [character]) -> [U] where U.SequenceCharacter == character{
guard validate(characters: characters) else {
return []
}
let lastNodeCharacters = getNodeFor(characters: characters)
if lastNodeCharacters == nil {
return []
}
var discoveredNodes:[(node: Node, char: character, counter: Int)] = DFS(node: lastNodeCharacters!, char: characters[characters.count - 1])
// discoveredNodes also includes the last character from characters parameter
// it can easily be removed here, since we know it's the first discovered node
discoveredNodes.remove(at: 0)
return buildWords(characters: characters, discoveredNodes: &discoveredNodes)
}As you can see, buildWords function takes as parameters the prefix and the sequence of discovered nodes from DFS.
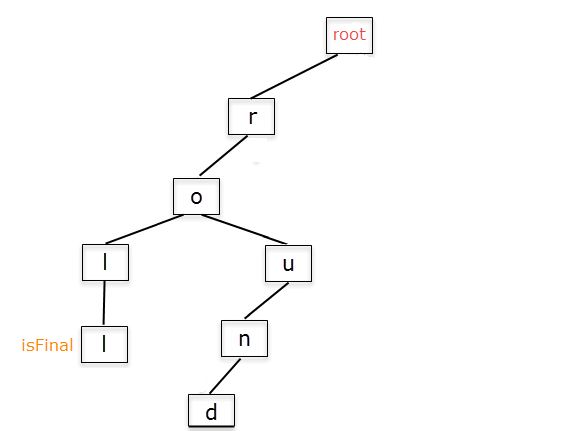
Consider the following Trie:
At a call of suggestWords("ro"), discoveredNodes will contain the following nodes in the order marked with red:
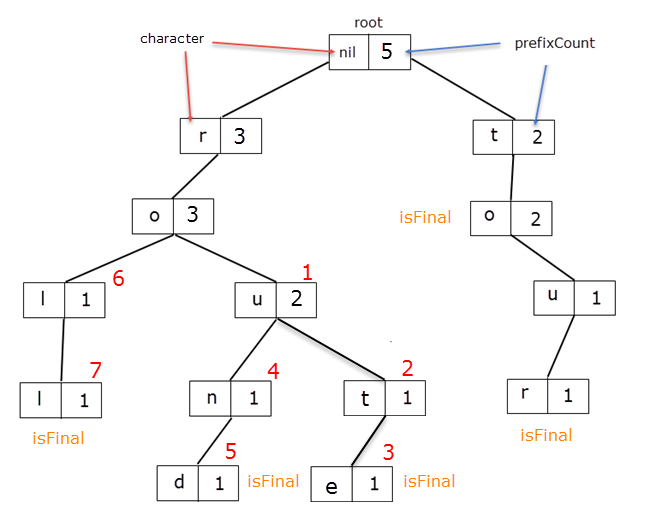
In the buildWords function we iterate discoveredNodes until we find a node for which isFinal is set to true.
When such node is found, we iterate once again from the beginning, but stopping at our initial node. Each node found along the way, having counter > 0, is included in the current word and counter is decremented, in order to indicate the limited number of usages.
Here's how the construction of the words "route" and "round" will go like:
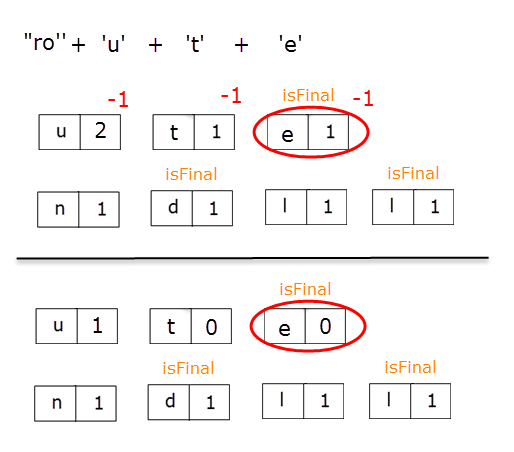
Bellow you have the code:
func buildSeq<U:CharacterSequence>(characters: [character], discoveredNodes: inout [(node: Node, char: character, counter: Int)]) -> [U] where U.SequenceCharacter == character {
var res:[U] = []
for i in 0..<discoveredNodes.count {
if discoveredNodes[i].node.isFinal == true {
var w:[character] = []
// counter tells us which nodes characters are to be included in the sequence
// if counter > 0 then the node's character belongs to the sequence and we decrement the counter
// otherwise, the node was used in other sequences and is now "used up"
print("building seq starting with:",characters)
for j in 0...i{
if discoveredNodes[j].counter > 0 {
print(discoveredNodes[j].char)
w.append(discoveredNodes[j].char)
discoveredNodes[j].counter -= 1
}
}
w = characters + w
res.append(U(characters: w))
}
}
return res
}I left 2 prints there to make clear at runtime how the algorithm works.
Test Run:
print (myTrie.suggestWords("ro"))will print:
building seq starting with: ["r", "o"]
u
t
e
building seq starting with: ["r", "o"]
u
n
d
building seq starting with: ["r", "o"]
l
l
["route", "round", "roll"]That's it :)
Remark: The algorithm does not return the prefix itself if it's a valid word in our dictionary
Code file: http://pastebin.com/Nm5iQMrz
Now, that we reached the ending, I hope the article made you see the importance and usefulness of the Trie data structure .
Practice, practice, practice :)