sile/pfds-ch6.md

## pfds-ch6.md

      
    Raw
  

              pfds-ch6.md
            
          
    6 遅延評価を使った償却と永続性

前章の題材:

償却というアイディアの提示
良い償却計算量を有するいくつかのデータ構造の紹介

償却の問題点:

永続性とは相性が悪い

この章では遅延評価が、どのように償却と永続性の衝突問題を緩和するかを説明する:

銀行員および物理学者の手法は遅延評価を考慮できるように改修
実例として内部で遅延評価を使ったデータ構造をいくつか取り上げる

6.1 実行追跡と論理時間

永続性がある場合の償却の問題点:

償却はユニークな未来を仮定している

想定: 蓄積された貯蓄は、一度だけ消費される
実際: 複数の論理未来が、同じ貯蓄を消費しようとするかもしれない


用語定義:

実行追跡(execution traces):

論理時間の形成要素であり、計算の歴史の抽象的なビューを与える
一つの実行追跡は、一つの有向グラフに対応

ノードは、対象となる操作を表す (ex. 対象データの更新操作)
vからv'への枝は、操作v'がvの結果を利用していることを表す


論理歴史(logical history):

操作vの論理歴史は^vと表記される

! gist上で書きにくいのでhist(v)と表記することもあります


論理歴史は、vの結果が依存するすべての操作の集合(v自身を含む)
言い換え: ^vは、wからvへのパスが存在する全てのノードwの集合


論理未来(logical future):

ノードvの論理未来とは、vから終端ノードへの任意のパスのことを指す
ひとつ以上のパスがある場合は、vは複数の論理未来を有している


便宜上、「オブジェクト」を「そのオブジェクトを生成した操作」の代わりに使用することがある

Exercise 6.1

![Exercise 6.1](http://g.gravizo.com/g?
digraph g {
a [label = "a = snoc<empty, 0>"];
b [label = "b = snoc<a,1>"];
c [label = "c = tail b"];
d [label = "d = snoc<b,2>"];
e [label = "e = c ++ d"];
f [label = "f = tail c"];
g [label = "g = snoc<d,3>"]
g -> d;
f -> c;
e -> c;
e -> d;
d -> b;
c -> b;
b -> a;
}
)

実行追跡は バージョングラフ(version graphs) の一般化:

バージョングラフは、永続データ構造の歴史群をモデリングするためによく使用される

ノード: 単一の永続アイデンティティに対応するバージョン群を表す
エッジ: バージョン間の依存関係を表す


バージョングラフは操作結果のモデル化であり、実行追跡は操作自身のモデル化
実行追跡の方が便利なことが多い:

複数の永続アイデンティティの歴史が結合可能
新しいバージョンを返さない操作(ex. queries)の推論にも使える
複数の結果を返す操作に関しても同様 (ex. splitting a list into two sublists)


実行追跡／バージョングラフにおける制限について:

短命データ構造の場合は、典型的には、ノードの出次数は最大で一つに制限される
多様な種類の永続性をモデル化するために、バージョングラフはノードの出次数に制限を設けない

ただし、以下のような制限がつくことが多い:

ex. グラフは木(森)に制限される: ノードの入次数は最大で一つ
ex. 入次数には制限がないが、循環は禁止される (DAGであることが要求される)


本書の実行追跡には、そのような制限は課さない:

入次数が一以上のノードは、複数の引数を取る操作に対応する
循環は、再帰的に定義されたオブジェクトで発生し得る (遅延評価言語では珍しくない)
一つのノードペアの間に複数のエッジが存在することも許す (ex. a list is catenated with itself)


実行追跡は、6.3.1節で、銀行員の手法を永続性を扱えるように拡張する際に使用される
6.2 償却と永続性を和解させる

節の目的:

銀行員／物理学者の手法が修復可能なことを示す

蓄積貯蓄は蓄積負債に置き換えられる
負債は未評価の遅延計算のコストを計測する
「貯蓄は一回しか消費できないけど、負債を複数回精算しても悪いことはないよ」とか何とか


6.2.1 遅延評価の役割

高価な操作:

償却コストよりも実際のコストの方が高い操作
f(x)が高価だと仮定して、

悪意のある敵対者はf(x)を無限回呼び出すかもしれない
=> 償却ケースではなく、最悪ケースの計算量になってしまう


f(x)の最初の呼び出しが高価なら、後続のf(x)の呼び出しは安価となることが保証されるような方法を見つける必要がある

遅延評価 + メモ化:

副作用がない場合は、以下の評価順序では高価な操作問題を解決できない:

call-by-value: i.e. strict evaluation
call-by-name: i.e. lazy evaluation without memoization
両者共にf(x)の各呼び出しが、完全に同じ時間量を消費するため


call-by-needが必要

i.e. lazy evaluation with memoization
二回目以降のf(x)呼び出しは、メモ化された結果を直接参照するので安価


Remark:

回顧的な観点からすれば、遅延評価と償却の関係は驚くようなものではない

遅延評価は自己書き換えの一種と見做せる
償却もしばしば自己書き換えを伴う


しかし、遅延評価は自己書き換えの、より規律化された形式である

全ての形式の、償却短命データ構造で典型的に使用されている自己書き換えが、遅延評価としてエンコードできる訳ではない
ex. スプレー木


6.2.2 遅延データ構造を解析するためのフレームワーク

解析用フレームワークの導入:

遅延評価は償却データ構造をpurely-functionallyに実装するためには不可欠

不幸なことに遅延評価が関わるプログラムの実行時間を解析することは悪名高いほど難しい
歴史的には、遅延プログラムを解析するための最もよくあるテクニックは、それらを実際には正格であるかのように見做すこと
しかし、このテクニックは遅延償却データ構造を解析するためには全く不適切


この章の残りでは、そういった解析をサポートするための基本的なフレームワークについて述べる

銀行員／物理学者の手法をこのフレームワークに適合させる
"yielding both the first techniques for analyzing persistent amortized data structures and the first practical techniques for analyzing non-trivial lazy programs"


与えられた操作のコストをいくつかのカテゴリに分類する:

非共有コスト(unshared cost):

仮定: 対象操作の開始時には、システム内の全てのサスペンションは既に強制(forced)およびメモ化済みであるものとする

この仮定のもとでは、対象操作内で作成および強制されるサスペンションを除き、強制は常にO(1)時間で行われる


対象操作の実行に要するであろう実際の時間


共有コスト(shared cost):

仮定: 上記のものと同様
対象操作によって作成されたが、評価はされない全てのサスペンションを実行するのに要するであろう時間

! 非共有コストとは異なり(対象操作内で実際に実行される訳ではないの)仮想的な時間


完全コスト(complete cost):

非共有コストと共有コストの合計
完全コストは、遅延評価が正格評価に置き換わった場合の対象操作の実際のコストを表している


さらに一連の操作群の合計共有コストを、以下の２つに分割する:

実現コスト(realized cost):

処理全体の中のどこかで実行されるサスペンション群の共有コスト


未実現コスト(unrealized cost):

決して実行されないサスペンション群の共有コスト


一連の操作群の 合計実際コスト(total actual cost) は「非共有コストと実現共有コスト」の合計となる:

未実現コストは実際のコストには寄与しない
特定の操作が合計実際コストに寄与する値は「非共有コストと完全コストの間のいずれか」となる

実際の値はその操作の共有コストがどの程度実現されたかに左右される


共有コストは 蓄積負債(accumulated debt) として説明される:

初期値はゼロ
サスペンションが生成される度に、蓄積負債を増加させる

増加値はサスペンション(および任意のネストしたサスペンション群)の共有コスト


各操作は蓄積負債の一部を清算する

ある操作の 償却コスト(amortized cost) は「(その操作の)非共有コストと(その操作によって)清算された蓄積負債額」の合計となる:

サスペンションは対応する負債が全て清算されるまで強制することは許可されない


Remark:

蓄積負債は、layaway plan(商品留め置き方式)、と似てるよ、とか
詳細は本を参照


サスペンションの生存期間上には三つの重要な瞬間が存在する:

生成された時、完全に清算された時、実行された時
証明の義務は、二番目の瞬間が三番目に先行することを示すこと
もし全てのサスペンションが強制される前に清算されているとすると

then 清算済み負債の合計額は、実現共有コストの上限であることになる
and therefore 合計償却コストは、合計実際コストの上限であることになる


この辺りのより詳細は6.3.1節で

遅延プログラムの実行時間を解析する際の最も難しい問題の一つは、複数の論理未来間の干渉について推論すること:

本書ではこの問題を、それぞれの論理未来についての推論の際に、そこにただ一つの未来しか存在しないように扱うことで回避する

サスペンションを作成する操作の観点から云えば、サスペンションを強制する論理未来は、自分自身でそのための清算を行わなければならない
もし二つの論理未来が同じサスペンションを強制したいと望んだならば、両方が個々にそれに対して清算を行う必要がある
この制限を別の観点から述べると以下のようになる:

サスペンションは、その負債が、現在の操作の論理歴史内で清算された場合にのみ、強制が許可される


この方法を使うと、時々負債に対して一回以上の清算を行ってしまうことがある

特定の計算を行うために要求される合計時間の過剰見積もりが発生し得る
しかし「特に害はない」かつ「解析のシンプルさのためなら小さな代償」である


6.3 銀行員の手法

銀行員の手法を蓄積貯蓄ではなく蓄積負債を扱えるように修正する:

クレジットをデビットに置き換える
各デビットはサスペンドされた仕事の定数合計量を表す
最初に与えられた計算をサスペンドする時:

その共有コストに比例するだけ多くのデビットを作成する
それぞれのデビットを対象オブジェクトの位置に対応させる


それぞれのデビットのための位置の選択は、その計算の性質(nature)に依存する

もし計算がモノリシックなら、全てのデビットは通常その結果のルートに割り当てられる
逆にもし計算がインクリメンタルなら、デビットはおそらく部分的な結果群の間で分配されるだろう


ある操作の償却コストは「その操作の非共有コスト + その操作によって支払われたデビットの数」となる:

操作によって作成されたデビットの数は、償却コストには含まれない
デビットが支払われるべき順序は、どのようにオブジェクトがアクセスされるかに依存する

すぐにアクセスされそうなノード上のデビットは、最初に支払いが行われるべき


償却境界(amortized bound)を証明するためには:

ある位置にアクセスする時はいつでも、その位置に関連付けられた全てのデビットが支払い済みであることを示さなければならない

デビットが支払い済み = サスペンドされた計算が完全に清算済み


これにより、一連の操作によって支払われたデビットの合計が、その操作群の実現共有コストの上限となることが保証される
従って、合計償却コストは、合計実際コストの上限となる

計算の終わりまで残ったデビットは未実現共有コストに対応し、それは合計実際コストには影響を与えない


インクリメンタルな関数は、銀行員の手法において重要な役割を果たす:

それらはデータ構造の異なる位置にデビットを散らばらせることを許可するため

それぞれはネストしたサスペンションに対応する


そして、各位置は自身のデビットが支払われたらすぐにアクセスを受け入れることができる

他の位置のデビットの支払いを待つ必要はない


実用上これは、インクリメンタルな計算の最初の部分結果は、極めて素早く清算可能であることを意味する

後続の部分結果は、それらの必要に応じて清算される


一方、モノリシックな関数は、より柔軟性が低い

プログラマは高価でモノリシックな計算の結果が必要とされるであろう時を予測する必要がある
そして、その結果が必要とされる時までに、全てのデビットが支払い可能なように、十分に前から計算を組み立てる必要がある


6.3.1 銀行員の手法の正当性を示す

この節では、合計償却コストが合計実際コストの上界であるという主張が正当であることを示す。

合計償却コスト: 合計非共有コスト + 支払済みデビットの合計
合計実際コスト: 合計非共有コスト + 実現共有コスト
=> 支払い済みデビットの合計が、実現共有コストの上限となっていることを示す必要がある

銀行員の手法は、6.1節の実行追跡を使うと、抽象的にはグラフのラベリング問題と見ることができる。
問題: 以下の性質を持つs(v)、a(v)、r(v)の三つのセットを伴う追跡上の全てのノードにラベルを付ける
cond_1(V, V)  -> ok;
cond_1(V, V_) -> [] = s(V) -- s(V_), ok.

cond_2(V) ->
  true =
    ordsets:is_subset(
      ordsets:from_list(a(V)),
      ordsets:from_list(lists:append([s(W) || W <- hist(V)]))),
  ok.

cond_3(V) ->
  true =
    ordsets:is_subset(
      ordsets:from_list(r(V)),
      ordsets:from_list(lists:append([a(W) || W <- hist(V)]))),
  ok.
s(v):

操作vに割り当てられたデビットの集合
条件1は、一つのデビットが複数回割当られることはないことを示している

a(v):

操作vによって支払われたデビットの多重集合
条件2は、以下を主張している

デビットは作成前に支払われることはない
=> ある操作は、自分の論理歴史上に現れるデビットに対してのみ支払いが可能


r(v):

操作vによって実現された(realized. 現金に換えられた？)デビットの多重集合

=> 操作vによって強制されたサスペンション群に対応するデビットの多重集合


条件3は、以下を主張している

デビットは支払い前に reallized されることはない
=> デビットは、現在の操作の論理歴史の中で支払い済みではない場合は、realized されることはない


何故、a(v)とr(v)は多重集合なのか？

一つの操作が同じデビットを複数回支払い(or 実現)することがあるため
望んで複数回支払うことはない

同じオブジェクト同士を結合しようとすると起こり得る
例:

リストの連結関数を解析しているとする
第一引数と第二引数のそれぞれに少数のデビットを支払うとする
仮にリストを自分自身に結合させようとしたら、そのリストのデビットを二回支払うことになる


ここまでの銀行員の手法の抽象的な観点から、計算の多様なコストを簡単に測定することができる:

Vを 実行追跡上の全てのノードの集合とする
合計共有コスト:

lists:sum([length(s(X)) || X <- V])


支払い済みデビットの数の合計:

lists:sum([length(a(X)) || X <- V])


実現共有コスト:

length(lists:usort([r(X) || X <- V]))
メモ化されるので、複数回強制されたサスペンションでも、実コストに寄与するのは一度だけ
メモ化無しなら:

RealizedBag = lists:sum([length(r(X)) || X <- V])


条件3から:

RealizedSet = lists:usort([r(X) || X <- V])はDiscardedSet = lists:usort([a(X) || X <- V])の部分集合
DiscardedBag = lists:sum([length(a(X)) || X <- V])
=> length(RealizedSet) =< length(DiscardedSet) =< length(DiscardedBag)


故に:

実現共有コスト is bounded by 支払い済みデビットの合計
合計実際コスト is bounded by 合計償却コスト
=> 期待通り


Remark:

メモ化は重要
メモ化がない場合は合計実現コストはRealizedBagになり、以下の式が成り立つ保証はない

length(RealizedBag) =< length(DiscardedBag)


6.3.2 例: キュー

効率的な永続キューを開発する:

銀行員の手法を使って、全ての操作がO(1)の償却コストで実行可能なことを証明する

5.2節のキューに対する変更点:

遅延評価を取り入れる必要がある

リストのペアを、ストリームのペアに置き換える
便宜上、それぞれのストリームの長さも保持しておく
type a Queue = int x a Stream x int x a Stream
フロントサイズ x フロントストリーム x リアサイズ x リアストリーム


リバースタイミング

旧: フロントが空になったら
新: 旧の方法だとreverse用のサスペンションを生産する時間がない

代わりに、定期的にキューを回転する
回転: 全てのリアストリームの要素を、フロントストリームの要素の末尾に移動する

fをf ++ reverse rで置換
新しいリアストリームは空に設定


この変更は要素の相対的な順序には影響を与えない


何故、回転しないといけないのか？

リバースはモノリシックな関数

その結果が必要になる十分に前から、全てのデビットを支払えるように計算を組み立てる必要がある


リバース処理は|r|ステップを要する

このコストを考慮して、|r|個のデビットを割当てる (今は++のコストは無視している)
リバースサスペンションが強制されるのは、早くても、|f|回だけtailが適用されてから

|r|≈|f|の時にキューを回転し、tailの度に一つのデビットを支払うなら、リバースの実行時には清算済みとなる


=> キューを回転するのは|f| < |r|になったタイミング

|f| >= |r|という不変項を維持する
付随的に「fが空になるのは、rも空の場合のみ」という保証もつく (5.2節のキューと同様)


実装(図6.1):
structure BankersQueue : QUEUE =
struct
  type a Queue = int x a Stream x int x a Stream

  val empty = (0, $NIL, 0, $NIL)
  fun isEmpty (lenf, _, _, _) = (lenf = 0)

  fun check (q as (lenf, f, lenr, r)) =
      if lenr =< lenf then q else (lenf + lenr, f ++ reverse r, 0, $NIL)

  fun snoc ((lenf, f, lenr, r), x) = check (lenf, f, lenr + 1, $CONS(x, r))

  fun head (lenf, $NIL, lenr, r) = raise EMPTY
    | head (lenf, $CONS(x, f'), lenr, r) = x

  fun tail (lenf, $NIL, lenr, r) = raise EMPTY
    | tail (lenf, $CONS(x, f'), lenr, r) = check(lenf - 1, f', lenr, r)
(歴史が複数ある場合に)リバースがどれだけ実行されるか?

分岐点Kを選択:

Kが回転の後なら:

サスペンションを共有するので強制回数に関係なく一回だけ実行
メモ化が大事だよ、ということの繰り返し


Kが回転の前なら:

それぞれの歴史でサスペンションは異なるので、メモ化は効かず、歴史の数だけリバースが実行される
ただし、回転の前なら、リバースの前に十分な数のtailの適用があり、デビットの支払いは完了しているので問題ない


キー: 仕事を複製するのは、その仕事のコストを償却するのに十分な操作列も同時に複製した場合のみ

永続環境化でもキューの各操作がO(1)の償却時間で実行可能なように見える。
銀行員の手法を使って、ちゃんと証明する。

全てのキュー操作の非共有コストはO(1) (by inspection)
よって、全てのキュー操作の償却コストがO(1)であることを示すためには、以下の証明が必要:

各操作毎のO(1)のデビット支払いは、全てのサスペンションを(強制前に)清算するために十分である


実際に、snocとtailのみがデビット支払いを行う

デビット不変項:

[定義] d(i):フロントストリーム上のi番目のノードのデビットの数
[定義] D(i): lists:sum([d(J) || J <- lists:seq(0, I)])

先頭からi番目のノードまでのデビットの数の累積


不変項:

D(i) =< min(2i, |f| - |r|)
2i部分が担保する保証:

フロントストリームの最初のノード上の全てのデビットは支払い済みである

d(0) = D(0) =< 2 * 0 = 0


=> 先頭に対してはいつでもheadやtailが適用可能


|f| - |r|部分が担保する保証:

二つのストリームの長さが等しいなら、キュー全体のデビットは支払い済みである
次の回転の直前に、この状況になる


定理6.1:

snocとtailは、それぞれ1と2のデビットを支払うことで、デビット不変更を維持する

証明:
ケース毎に分析
回転につながらないsnoc:

単に新しい要素をリアストリームに追加するだけ

|r|が一増加 => |f|-|r|は一減少
これは、もともとD(i) = |f|-|r|であった全てのノードの不変項を破壊する

キューの先頭のデビットを支払うことで、不変項を回復可能
後続の全てのサブシーケンスの累積デビットを一減少させるため


回転につながらないtail:

単にフロントストリームから要素を取り除くだけ

|f|が一減少 => |f|-|r|は一減少
より重要なのは、後続の全ての要素のインデックスが一小さくなること

2iが一つ分小さくなるので、D(i)は二減少する


キューの先頭二つのデビットを支払うことで、不変項は回復する


回転につながるsnocおよびtail:

前提: 回転の直前では、キュー上の全てのデビットが支払い済みであることは保証されている

=> 回転の後で弁済されていない(undischarged)デビットは、回転自体によって生成されたもののみ


回転時に|f| = m and |r| = m + 1とする:

生成されるデビット:

結合用のm個
リバース用にm+1個


結合関数はインクリメンタル:

最初のmノードに、それぞれひとつずつデビットを割当てる


リバース関数はモノリシック:

全てのm + 1デビットを、ノードm(リバース後の先頭ノード)に全て割当てる


まとめると(回転後の)デビットは以下のように分配される:
d(I, M) when I  < M -> 1;
d(I, M) when I == M -> M + 1;
d(I, M) when I  > M -> 0.

large_d(I, M) when I  < M -> I + 1;
large_d(I, M) when I >= M -> 2 * M + 1.
この分配は0とmのノードの不変項を破壊するが、両方共、ノード0のデビットを支払うことで回復する。

この議論(argument)の形式は典型的:

分配方法:

インクリメンタルな関数では、デビットは複数のノードに跨って分配される
モノリシックな関数では、一つのノードにまとめられる


(不変項で考慮される)デビットのカウント方法:

対象ノードだけではなく、ルートから対象ノードに至るパス上の全てのノードのデビットが含められる
あるノードにアクセスするのには、その前に、その祖先全てにアクセスする必要がある、という事実を反映している

経路上の全てのノードのデビットも同様に0である必要がある


このデータ構造は、ネストしたサスペンションの微妙な点も描いている:

ネストしたサスペンション用のデビットは、そのサスペンションが物理的に生成される前に、割当られて支払いまで行われるかもしれない
例:

++がどう動くか
ストリーム内の二番目のノードのサスペンションは、最初のノードのサスペンションが強制されない限りは、物理的には生成されない
しかし、メモ化により、二番目のノードのサスペンションは、最初のノードのサスペンションが共有される時は、いつでも同様に共有される
そのため、(we consider)ネストしたサスペンションは、包含するサスペンションが生成された時に、暗黙的に生成されると考える
さらに、デビット主張(argument)やオブジェクトの形に関する他の推測について考慮する時は、そのノードが既に物理的に生成されているかどうかは無視する
それよりは、全てのノードの形が最終形であるものとして推論を行う

i.e. 対象オブジェクトの全てのサスペンションが強制済みであるかのように


Exercise 6.2

https://github.com/sile/erl_pfds/blob/master/memo/ch06_exercise.md
6.3.3 デビット継承

本体で他の既存のサスペンション群を強制するようなサスペンションを作ることが良くある:

新しいサスペンションは古いサスペンション群に 依存している

キューの例:

reverse rによって作成されたサスペンションはrに依存している
f ++ reverse rによって作成されたサスペンションはfに依存している


サスペンションを強制する時は、自分のものだけではなく、自分が依存するサスペンションも全て支払われているようにしなければならない

キューの例:

デビット不変項は、以下を保証している:

++を使って新しいサスペンションを生成する
既存のサスペンションが完全に清算された時にのみリバースする


However, we will not always be so lucky

未払いのデビットを持つ既存サスペンションに依存する新しいサスペンションを作成したい時はどうするか？

それらのデビットを新しいサスペンションに再割当てする

=> 継承 と呼ぶ


We may not force the new suspension until we have discharged both the new suspensiton's own debits and the debits in inherited from the older suspension
銀行員の手法は、両者のデビットに特に違いを設けてはいない (両方共新しいサスペンションに属するものとして扱う)
9,10,11章では、デビット継承をデータ構造解析のために用いる

Remark:

デビット継承は、古いサスペンション群へのアクセス方法が、新しいサスペンションを通してしか行えないことを想定している
次の例ではデビット継承は解析のために使えない: fun reverseSnd(xs, ys) = {reverse ys, ys}

次のいずれかの方法を取る:

a. ysのサスペンションを複製して、新しい方にはそれを割当てる
b. 一つのデビットを共有して、明示的に依存性を追跡する


6.4 物理学者の手法


復習:
val s = $primes 10000 (* create suspention *)
val $x = s (* force *)

(* 以下の二つの式は等価 *)
fun lazy f p = e
fun f x = $case x of p => force e

accumulated savingsではなく、accumulated debtを使う:

何が違うか？

後者はpay off済みのサスペンションしかforceできない (永続性との兼ね合い)
重い処理を実行したい場合は、以下の二つが満たされている必要がある

重い処理の前に、それを償却するに足るだけの十分な数の軽い処理を挟めるようにする
重い処理のサスペンションを以降の全ての歴史の枝で共有するようにする


償却コスト:

Ψで表す
ある操作の償却コスト:

complete_cost - change_in_potential

complete_cost: unshared_cost + shared_cost


ある時点でのポテンシャルとは「オブジェクト全体をforceした場合に掛かる(未清算)コストの総計」と考えることができる
参照系操作: クエリのような返り値にオブジェクト自身が含まれない操作

「償却コスト == ポテンシャル + unshared_cost」となる
オブジェクトの情報を取得するのでforceは必要 (原則として)
物理学者の手法はmonolithicなので、forceの際には常に全体に適用される
! このため(何も工夫をしないと)参照系のコストが高くなりがち


更新系操作:

オブジェクトの情報取得は不要(と仮定)なので、ポテンシャルの差分についてだけ考慮すれば良い
ポテンシャルに変化がない場合: 「shared costを全部即座に清算した」ことを意味する (ex. その関数内でforce)
ポテンシャルが増加した場合: 「shared costの清算を(増加分だけ)ペンディングした」ことを意味する
ポテンシャルが減少した場合: 「現在分 + 過去にペンディングされたshared costを(減少分だけ)清算した」ことを意味する


物理学者の手法はmonolithicなデータ構造しか扱えない:

銀行員の手法のようなlocationの概念がないため

less powerful (but much simpler)


6.4.3節では「以降の章では物理学者の手法はほとんど使わない」的なことが書かれている

6.4.1 例: 二項ヒープ

ポテンシャル関数に関しては省略。本を参照。
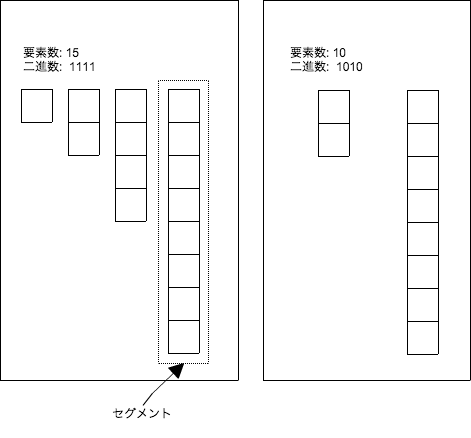
insert関数がちゃんと永続環境でも上手く定数償却コストで動作するのかを見てみる。
上手くいかなそうなケース:


二進数表現が「0111111111」になるようなヒープを作る


ここで歴史を分岐し、それぞれで以下を実行する


要素を追加する => 二進数表現は「1111111111」になる


さらに要素を追加する => 二進数表現は「00000000001」になる


各歴史で、link操作がlog(N)回実行されるのでO(1)ではなくO(log(N))にならないか？


(* insert関数の定義(二番目) *)
fun insert(x, ts) = $insTree (Node (0, x, []), force ts)
重要なのは「insert関数を何回呼び出してもサスペンションが蓄積されるだけで評価はされない」ということ:

一つの歴史のinsert関数列だけを見れば、一時的にポテンシャルが高くなる(最大でO(log(N)))ことはあっても、長期的に見れば償却されている
途中で参照系の関数が混ざったら、それはポテンシャル分の対価を払う必要があるので、参照系は軒並みO(log(N))に

関連: Exercise 6.5 (empty関数の償却コストがO(log(N))になった)


つまり以前の実装と本質的にことなるのは「insert関数が丸ごとlazyになっている」という点だけ:

insertだけを呼ぶ分には、forceされる可能性がないので、永続性時の歴史分岐の問題を気にする必要がない
(forceを実行する)参照系の操作が償却コストの悪化を肩代わり

Exercise 6.3

本質的に処理内容は変わっていないので、以前と同じ証明で十分
Exercise 6.4

lazyを外すことで、deelteMinやmergeも、insertのコストを肩代わりしなければならなくなるが、
もともとこれらの関数はO(log(N))の償却コストなので、結果に変わりはない。
Exercise 6.5

自明なので省略
6.4.2 例: キュー

要点:

type a Queue = a list(* front cache *) x int(* front size *)x a list susp x int(* rear size *) x a list
サスペンションするのはフロントリストだけ
リバースタイミングはフロント >= リアーが崩れた時

ポテンシャル関数に関しては省略。本を参照。
永続環境でも上手く行く(全操作がO(1)償却コスト)理由:

フロントキャッシュを用意しているので、二項ヒープのように参照系が重くなることがない
フロントのリバースはサスペンション内で行っているので、歴史間で共有可能

サスペンションの作成直前に歴史が分岐した場合は、共有不可能
ただし、その場合は、そのサスペンションがforceされるまでに十分償却可能 (銀行員の手法の場合と同様)


Exercise 6.6

何故、以下の最適化がO(1)の償却コストを壊してしまうのかを述べよ。
(a)


リバースサスペンション作成時にフロントをforceして、結果をキャッシュに格納しているけど、
キャッシュが空になった場合にだけforceするようにした方が遅延度が上がってより良いのでは？

このように変えた場合「リバースサスペンションがforceされるのがlength(f)回のtail関数適用後」という条件がなくなり、コストを償却できないケースが生まれる:

キャッシュサイズ=5, フロントサイズ=5、リアサイズ=0、の状況があるとする
snocを100回呼び出す => キャッシュサイズ=5, フロントサイズ=沢山(100くらい)、リアサイズ=少し、になる
tailを5回呼び出す => 償却できていないのに、フロントサイズ分のリーバス(+結合)が一気に走る

(b)


tail関数の中で $tl(force f) を毎回呼び出しているけど無駄では？
(create/force suspentionはO(1)だけど、馬鹿にできない定数項)
fは変えないで、lenf を減らすことで要素の減少を表すのが良さそう。

suspentionを作らないと shared_cost にできないのが問題:

フロントサイズ=10、リアサイズ=0、とする
tailを9回呼び出す
ここで歴史が分岐する
各歴史でtailを呼び出す

それぞれで drop 10 (force f) の呼び出しが発生するがdrop 10の部分は共有されていない
償却コストがO(N)になる


6.4.3 例: 共有付きのボトムアップマージソート

マージソートの例:

後続の章では銀行員の手法を使うことがほとんどなので、物理学者の手法の例をもう一つ載せておく

動機:

xsが既にどこかの歴史でソート済みなら、x :: xsをソートする際に、xsの部分を重複して処理したくはない

xの追加コストはO(log(N))にしたい
xs @ zsとys @ zsのような場合も同様
共有されている末尾部分は効率的に処理したい


ソート可能コレクションのシグネチャ:
signature SORTABLE =
sig
  structure Elem : ORDERED

  type Sortable

  val empty : Sortable
  val add   : Elem.T x Sortable -> Sortable
  val sort  : Sortable -> Elem.T list
end
ソート可能コレクションは平衡二分探索木で実装可能:

addはO(log(N))、sortはO(N)、の最悪時間で実行可能
今回はボトムアップマージソートを使って実装し、同様の(償却時間)オーダーを実現する

ボトムアップマージソートの図: 


ボトムアップマージソートを使ったソート可能コレクションの構造について:

二項ヒープと同様に、要素数の二進数表現とデータ構造が対応している


実装:
functor BottomUpMergeSort (Element: ORDERED): SORTABLE =
struct
  structure Elem = Element

  (* 一番目のフィールドには要素数を保持する *)
  type Sortable = int * Elem.T list list susp

  (* 何の変哲もない二つのリストのマージ処理 *)
  fun mrg ([], ys) = ys
    | mrg (xs, []) = xs
    | mrg (xs as x :: xs', ys as y :: ys') =
       if Elem.leq (x, y) then x :: mrg (xs', ys) else y :: mrg (xs, ys')

  val empty = (0, $[])

  (*
    二項ヒープのマージとほぼ同じ構造:
    - 要素数のニ進数表現で考える (数値のインクリメントに等しい)
    - 下位ビットから初めて、値が1の間はマージを行い、0ビットに到達するまで続ける
    - 0ビットに到達したら、そこの値を1に変更して終了
  *)
  fun add (x, (size, segs)) =
       let fun addSeg (seg, segs, size) =
                if size mod 2 = 0 then seg :: segs
                else addSeg (mrg (seg, hd segs), tl segs, size div 2)
       in (size+1, $addSeg ([x], force segs, size)) end (* 最初のaddSeg呼び出しはlazy *)

  (* foldlを使ったコードの方が簡潔なので、そちらを掲載 *)
  fun sort (size, segs) = foldl (mrg, [], force segs)
end

償却時間の話


addがO(log n)、sortがO(n)、であることを示したい

ポテンシャル関数:
Ψ(n) = 2 * n - 2 * sum([(n mod 2^i)) + 1 || i <- 0..bit_length(n), bit(n,i)==1])

性質:
- 上限: 2n
- `n = 2^k - 1`なら`Ψ(n) = 0`(kは任意の整数)

ポテンシャル関数の意味:

! 前回分からの引用: ある時点でのポテンシャルとは「オブジェクト全体をforceした場合に掛かる(未清算)コストの総計」と考えることができる

ポテンシャルが大きいということは、未清算のサスペンションが溜まっている、ということを表す


それぞれのセグメントが「自分自身のサイズ - より小さい全てのセグメントのサイズ合計」に比例するポテンシャルを保持することを反映

sort関数内で実行されるマージ処理のコストを反映している

各段階でのmrg(a, b)の:

a: その段階以前の全てのセグメントがマージされたリスト: size = n mod 2^i
b: その段階のセグメント: size = 2^i


! 詳しくはsort関数の償却コストのところで


直感的には、


セグメントのポテンシャルは大きな値から始まる


コレクションに要素が追加されていくに従い小さくなっていく (少しずつ清算されていく)


そのセグメントが別のセグメントとマージされる直前に、ポテンシャルはゼロに到達する


"you do not need to understand the origins of a potential function to be able to calculate with it"

addの場合

complete-cost:

unshared-costは1
shared-costはaddSegでのマージのコスト

k個の下位ビットが1なら、k回のマージが実行される
最初は1要素のリスト同士をマージ、次は2要素のリスト同士を...、次は4要素...
一回のマージのコストは2m (mは対象となるリストの片方の要素数)
shared-cost: (1 + 1) + (2 + 2) + ... + (2^(k-1) + 2^(k-1)) = ..略.. = 2 * 2^(k-1)
complete-cost: 2 * 2^(k-1) + 1 = 2^(K+1) - 1


償却コスト:

物理学者の手法における償却コストはcomplete_cost - change_in_potential
change-in-potential(途中):

nは追加の要素数、n'は追加後の要素数(= n+1)
Ψ(n') - Ψ(n)
...本の通りに展開/変換...
= 2 + 2 * sum([δ(i) || i <- 0..bit_length(n')])


δ(i):

定義: bit(n,i)*((n mod 2^i + 1) - bit(n',i)*(n' mod 2^i + 1)
三つのケースを考える:

i < k:

定義上bit(n,i) == 1,  bit(n',1) == 0が成り立つ
δ(i)= (n mod 2^i) + 1

(n mod 2^i) = 2^i - 1


= (2^i - 1) + 1 = 2^i


i = k:

定義上bit(n,i) == 0, bit(n',1) == 1が成り立つ
δ(i)= -(n' mod 2^k) - 1

(n' mod 2^k) = 0


= -1 = -bit(n', i)


i > k:

定義上bit(n,i) == bit(n',i)が成り立つ
δ(i)= bit(n',i) * (n mod 2^i - n' mod 2^i)

n' mod 2^i = (n+1) mod 2^i = n mod 2^i + 1


= bit(n',1) * ((n mod 2^i) - (n mod 2^i + 1))
= -bit(n',i)


change-in-potential(完成):

= 2 + 2 * sum([δ(i) || i <- 0..bit_length(n')])
= 2 + 2 * sum([2^i || i <- 0..(k-1)]) + 2 * sum([-bit(n',i) || i <- k..bit_length(n')]
= 2 + 2 * (2^k - 1) - 2 * sum([bit(n',i) || i <- k..bit_length(n')]
= 2^(k+1) - 2*number_of_one_bits(n')


償却コスト:

= complete_cost - change_in_potential
= (2^(K+1) - 1) - (2^(k+1) - 2*number_of_one_bits(n'))
= 2 * number_of_one_bits(n') - 1
number_of_one_bits(n')はO(log(n))なので、add関数の償却コストもO(log(n))


sortの場合

! 最初のforceを除いて、あまり遅延や償却云々は関係ない
以下の二つを考慮する:


最初のforce segsのコスト


このソート関数はquery系であり、ポテンシャル分をコストに加算する必要がある
Ψ(n)の最大値は2nなので、O(n)上界となる


segsのマージに要するコスト


最悪ケースを考える
n = 2^k - 1の場合 (二進数表現の場合は、全てのビットが1)
合計k回のmrg呼び出しがあり、小さい方から順番に隣接するセグメントをマージしていく
マージコスト:

(0 + 1) + (1 + 2) + (1 + 2 + 4) + (1 + 2 + 4 + 8) + ... + (1 + 2 + ... + 2^(k-1))
...省略...
= 2n - k - 1
= = O(n)


両方のコストを考慮するとO(n) + Ψn)であり、全体もO(n)となる

Exercise 6.7: ストリームのリストに内部表現を変更してみよう

functor BottomUpMergeSort (Element: ORDERED): SORTABLE =
struct
  structure Elem = Element

  type Sortable = int * Elem.T Stream list

  val empty = (0, [])

  fun mrg ($NIL, ys) = ys
    | mrg (xs, $NIL) = xs
    | mrg (xs as $CONS(x, xs'), ys as $CONS(y, ys')) =
       if Elem.leq (x, y) then $CONS(x, mrg (xs', ys)) else $CONS(y, mrg (xs, ys'))

  fun add (x, (size, segs)) =
       let fun addSeg (seg, segs, size) =
                if size mod 2 = 0 then seg :: segs
                else addSeg (mrg (seg, hd segs), tl segs, size div 2)
       in (size+1, addSeg ($CONS(x, $NIL), segs, size)) end

  fun sort (size, segs) = foldl (mrg, $NIL, segs)

  fun take_smallest (k, segs) = take(sort segs, k)
end
(a) 銀行員の手法を使って、addとsortの償却コストを証明せよ

! 以下、境界的な数値の扱いは怪しい (だいたいの雰囲気で)
add


unshared_cost: O(log(n))
一つのセグメントに関するデビット分配:

二つのセグメントをマージのマージ時に、2 * segment_sizeだけのデビットを分配して遅延させる

2 * segment_sizeの(遅延された)新しいセグメントができる
実際には、新しいセグメントの各要素に1つずつデビットを分配する


新しいセグメントのマージが次の行われるのは、2 * segment_size回だけadd関数が呼ばれた後

add関数呼び出し毎に、1つのデビットを精算する


これを全てのセグメントに適用する

add関数呼び出し毎にnumber_of_one_bits(n)のデビットが清算される
number_of_one_bits(n) = O(log(n))


償却コスト: O(log(n)) + number_of_one_bits(n) = O(log(n))

※ mrg関数呼び出し毎に二つのデビットを支払うようにする、とした方が分かりやすいかも？ (よりインクリメンタル)
sort


unshared_cost: O(n)
デビット清算:

残っている全デビットを精算する
各要素には最大で1つのデビットが割り当てられている
そのため清算コストはO(n)となる


償却コスト: O(n) + O(n) = O(n)

(b) take_smallest(k,segs)の償却コストがO(k log n)であることを証明せよ


各セグメントは(遅延的に)先頭要素が一番小さい値を保持している


全体で一番小さい要素を決定するのは、全てのセグメントを(遅延的に)マージして先頭要素を取得する必要がある


ストリーム全体のマージ処理は遅延されるので、各セグメントの先頭要素のマージ処理だけを考えれば良い
先頭だけで良いのでnumber_of_one_bits(n)のmrg呼び出しが実際に行われることになる
= O(log(n))


同じことを(各セグメントでの対象要素を一つずつシフトさせながら)k回繰り返す


= O(log(n)) * k = o(k log n)


※ sort時のように全体のデビットを最初に精算することはできないため、各mrg関数呼び出し毎に二つのデビットを支払うようにする
※ 全体の償却計算量には影響なし
6.5 遅延ペアリングヒープ

5.5節のペアリングヒープを永続化に対応させた:

不運なことに、永続版もオリジナルと同様に解析が困難なことは変わらない
元のものと（漸近的に)同じくらい効率的であると推測する

変更点:

以前は子ヒープをリストで保持していた

これだと(下記掲載の)マージ関数が永続化に対応できない
(mergePairsを使っている)deleteMin関数が複数回呼ばれると期待した償却効率を達成できない


遅延評価を活用するために、子の保持方式を以下のように変更する

新: Elem.T x Heap x Heap susp
旧: Elem.T x Heap list
明示的なconsに分解して、cdr部分を遅延させた感じ


(* old version *)
fun mergePairs [] = E
  | mergePairs [h] = h
  | mergePairs (h1 :: h2 :: hs) = merge (merge (h1, h2), mergePairs h2)
実装:
functor LaxyPairingHeap (Element: ORDERED): HEAP =
struct
  structure Elem = Element

  datatype Heap = E | T of Elem.T x Heap x Heap susp

  val empty = E

  fun isEmpty E = true
    | isEmpty _ = false

  (* 以下の二つは以前とほぼ同様 *)
  fun insert (x, a) = merge (T (x, E, $E), a)

  fun findMin E = raise EMPTY
    | findMin (T (x, a, m)) = x

  (* 以前はdeleteMin関数が複雑だったが、今回はmerge関数に複雑さが移った *)
  fun deleteMin E = raise EMPTY
      deleteMin (T (x, a, $b)) = merge (a, b)

  (*
    suspentionを制御するlink関数呼び出しが入ったことを除けば、以前とほぼ同様
    要素を比較して、小さい方をルートに設定する
   *)
  fun merge (a, E) = a
    | merge (E, b) = b
    | merge (a as T (x, _, _), b as T (y, _, _)) =
         if Elem.leq (x, y) then link (a, b) else link (b, a)
(* 以前: if Elem.leq (x, y) then T(x,h2::hs1) else T(y,h1::hs2) *)


  fun link (T (x, E, m), a) = T (x, a, m)  (* Eがあるなら、mをforceしないで持ち回す *)
      link (T (x, b, m), a) = T (x, E, $mergePairs(a, b, m))

  fun mergePairs(a, b, m) = merge (merge (a, b), force m) (* force m は、前回遅延されたmergePairs処理を強制する (lazy/forceによる再帰の模倣) *)
end
実践者へのヒント:

償却コストは同じだけど、遅延評価のオーバヘッドがあるから、実際には以前のものより遅い
しかし

永続化をヘビーに活用しているような用途では、メモ化の恩恵は大きい
遅延評価しかない言語でも有用

"where all data structures pay the overheads of lazy evaluation regardless of whether they actually gain any benefit"


6.6 チャプターノート

省略