memo: スケジューリングの役割
- イメージ的には銀行員の手法での__支払い__を実装に反映した感じ
- 後ろに重いサスペンションが控えている場合の挙動の違い:
- 6章(償却):「軽い操作で__仮想的に__その内のN個のデビットを払ったことにしておこう」
- 7章(最悪):「軽い操作で__実際に__その内のN個の(小さな)サスペンションを事前に評価しておこう」
- 支払い(or 評価)が終わっていないオブジェクト(サスペンション)に対するアクセスは許可されない
省略
省略
目的:
- 遅延二項ヒープ(6.4.1)では挿入コストが__償却__で
O(1)だったのを、__最悪__でO(1)にする
基本的な流れ(他の箇所と同様):
- モノリシックなデータ構造(list)から、インクリメンタルなデータ構造(stream)への変換
- スケジュールの導入
変更内容:
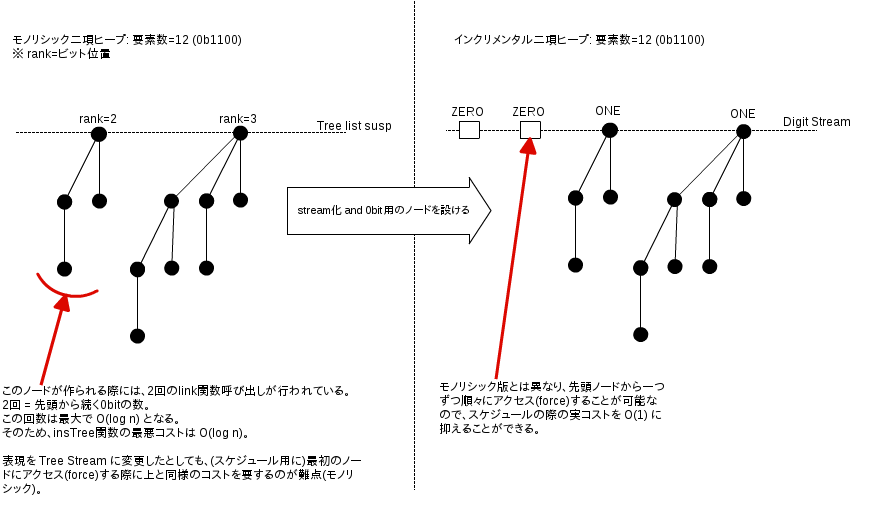
- 一番上の遅延リストをストリームに変更 (ノード単位で遅延可能)
- 0bitを表すノードの導入
- 旧版で仮想的な接頭0bitをスキップするために必要だった
O(log n)の再帰(モノリシック)部分が除去可能となった
- 旧版で仮想的な接頭0bitをスキップするために必要だった
もともと(6.4.1)のモノリシックな実装:
(* データ定義: Heapは一番外側のsusp以外は非遅延かつモノリシック *)
datatype Tree = NODE of int x Elem.T x Tree list (* rank(ビット位置) x elem x children *)
type Heap = Tree list susp (* 数値表現の1bitに対応するツリーだけを保持する *)
(* insTree関数: 遅延を含まないので log(N) の実コストが掛かる *)
fun insTree (t, []) = [t]
| insTree (t, ts as t' :: ts') =
if rank t < rank t' then t :: ts else insTree (link (t, t'), ts') (* この再帰で O(log n) 必要 *)本節でのインクリメンタルな実装:
(* データ定義 *)
datatype Tree = NODE of Elem.T x Tree list (* ビット位置の情報が不要となった *)
datatype Digit = ZERO | ONE of Tree (* 0bitの概念を導入するために一階層増えた *)
type Heap = Digit Stream
(* insTree関数: インクリメンタル版 *)
fun lazy insTree (t, $NIL) = $CONS (ONE t, $NIL)
| insTree (t, $CONS (ZERO, ds)) = $CONS (ONE t, ds)
| insTree (t, $CONS (ONE t', ds)) =
$CONS (ZERO, insTree (link (t, t'), ds)) (* 全ての関数節が再帰を挟まずに遅延可能になった *)データ定義の修正およびinsert関数にスケジュール管理を追加:
- スケジュールはジョブのリスト
- 各ジョブの型は
Digit Streamで、これは「insTree呼び出しの未実行部分」を表す
- 各ジョブの型は
- insert関数の償却コストは
2だった(6.4.1)ので、各呼び出しに付き二回のスケジュール実行を行えば良い
(* データ定義 *)
type Schedule = Digit Stream list
type Heap = Digit Stream x Schedule
(* スケジュール実行関数 *)
fun exec [] = [
| exec (($CONS (ONE t, _)) :: sched) = sched (* 1bit部分に達したので遅延されたinsTree呼び出しは実行完了 *)
| exec (($CONS (ZERO, job)) :: sched) = job :: sched (* 先頭一つ分の0bitをスキップ *)
(* memo: `job`は、insTree内の`insTree(link(t,t'), ds)`(の結果)に対応し、このパターンマッチはこの(遅延されていた)式を実行するに等しい *)
(* insert関数 *)
fun insert (x, (ds, sched)) =
let val ds' = insTree (NODE (x, []), ds) (* 通常通りinsTreeを呼び出して、遅延ストリームを取得する *)
in (ds', exec (exec (ds' :: sched))) end (* 二回分スケジュールを実行する *)実装変更は完了。
insert関数の最悪コストがO(1)であることを示すために必要なことは?
- 内部で呼んでいる
insTreeとexecの両方がO(1)であることを示す必要がある insTreeのunshared-costはO(1)であることが自明 (lazy付きで宣言されているため)execは常に二回呼びだされる:- 各呼び出しのコストが
O(1)なら全体もO(1) execのパターンマッチでforceされるサスペンションの依存先が既にforce済みなら、execの実行コストはO(1)- 依存先:
- 各サスペンションは、同じインデックス(ビット位置)の以前のサスペンションに依存している
- 依存先が常に評価済みであることの証明は定理7.1で行う
- 各呼び出しのコストが
# サスペンションの依存の例
init : 0
add-1: 1
add-2: 0 1
add-3: 1 1
add-4: 0 0 1
add-5: 1 0 1
add-6: 0 1 1
add-7: 1 1 1
add-8: 0 0 0 1
↑
例えばスケジュールを使わずに、連続して8要素を(遅延)追加後に、先頭要素を取得しようとすると、
その依存先(同じビット位置 = 0bit目)の遅延されていた処理が一度に実行されてしまう。
(この例だとforceが7回再帰的に呼ばれ、その中でlinkが四回実行される)
用語定義:
- 範囲(range):
- ジョブに対応するdigit列
- 各__範囲__は
ZERO*ONEのdigit列を含む (! 正規表現) - 評価済みのdigitはスケジュール(ジョブ)からは抜けるので__範囲__には含まれない
- 例:
- 一度も
execが適用されていないジョブの__範囲__に含まれるインデックス0..mとなる (m = ONEのインデックス) - 二回
execが適用された後のジョブの__範囲__に含まれるインデックスは2..mとなる (m >= 2 が前提)
- 一度も
- オーバーラップ:
- 二つのジョブの__範囲__内のdigit列のインデックスに重複がある状態を表す呼称
- __オーバーラップ__が存在するということは、依存先が未評価のサスペンションが存在する、ということ
- そのため__オーバーラップ__が存在しないことを証明する必要がある (定理7.1)
- 定義上、__オーバーラップ__が存在しないのであれば、ヒープ全体での未評価のサスペンションは最大で
O(log n)となる
- 完了ZERO(completed zero):
- ストリーム内の対応するセルが既に評価(and メモ)されているZEROのこと
全ての有効なヒープは、以下の条件を満たしている:
- スケジュール上での最初の__範囲__の前方に、少なくとも二つの__完了ZERO__を有している
- スケジュール上で隣接する二つの__範囲__の間に、少なくとも一つの__完了ZERO__を有してる
- ! これが__オーバーラップ__がないことを保証している
定義:
- r1とr2: スケジュール内の最初の二つの__範囲__
- z1とz2: r1より前の二つの__完了ZERO__
- z3: r1とr2の間の__完了ZERO__
- r0: これから追加される新しい__範囲__
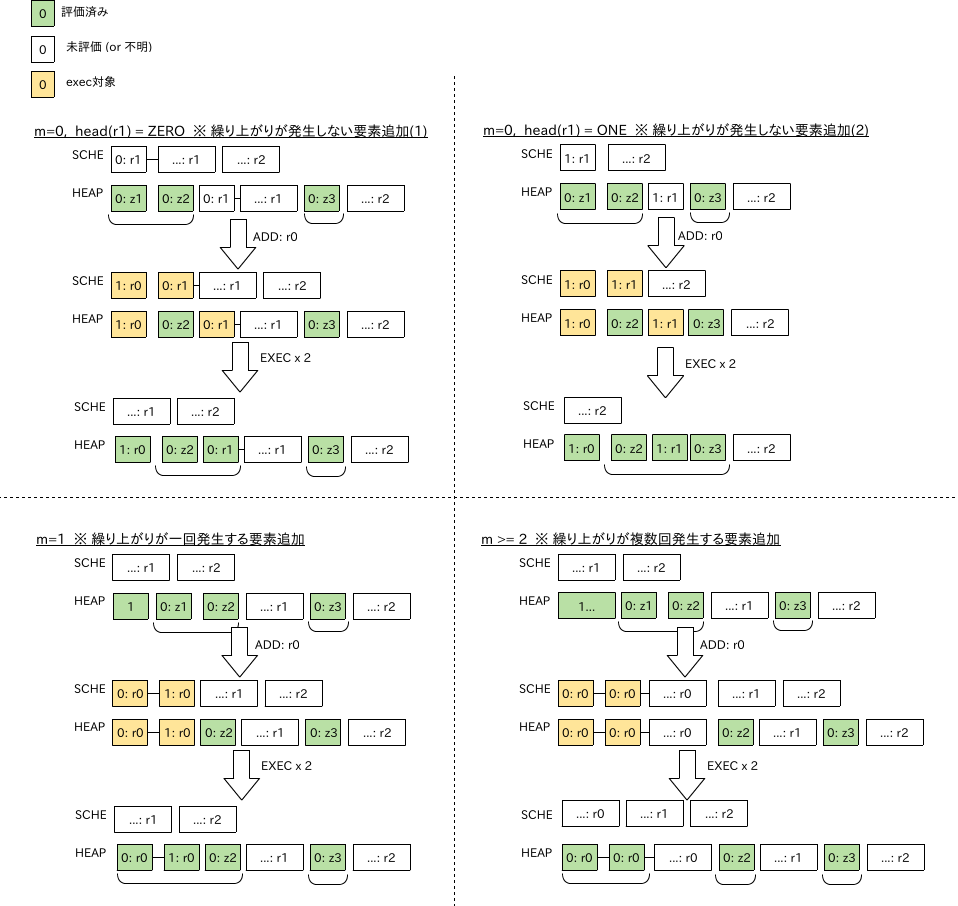
- insert関数は、スケジュールの先頭にr0を追加し、すぐに
execを二回呼び出す - NOTE: r0の終端のONEは、z1を置換する
- insert関数は、スケジュールの先頭にr0を追加し、すぐに
- m: r0内のZEROの数
ケース分析:
- ケース1: m = 0
- r0内の唯一のdigitはONE
- r0は最初の
execで除去される - 次の
execはr1の最初のdigitをforceする - もしそれがZEROなら、それは最初の__範囲__より前の二番目の__完了ZERO__となる (一番目はz2)
- もしそれがONEなら、r1は除去されてr2が最初の__範囲__となる
- r2に先行する二つの__完了ZERO__はz2とz3
- ケース2: m = 1
- r0内の二つのdigitはZEROとONE
- 二回の
execによってr0は除去される - 先頭のZEROはz1の代わりに、r1の前の二つの__完了ZERO__の一つとなる
- ケース3: m >= 2
- r0の最初の二つのdigitはZERO
- 二回の
execの後に、それらは(新しい__範囲__であるr0の残り部分の前方の)二つの__完了ZERO__となる - z2はr0とr1の間の単一の__完了ZERO__となる
! __範囲__がスケジュール上に存在しない場合のケースが記述されていないのは、そもそも__範囲__が二つ未満なら__オーバーラップ__が発生し得ないため
問: insTree関数から
lazy宣言を外しても実行時間には悪影響を与えないことを示せ
lazyの有無で実装を比較してみる:
(* lazy有り版の展開形 *)
fun insTree (t, ds) =
$case ds of
$NIL => CONS (ONE t, $NIL)
| $CONS (ZERO, ds') => CONS (ONE t, ds')
| $CONS (ONE t', ds') => CONS (ZERO, insTree (link (t, t'), ds'))
(* lazy無し版 *)
fun insTree (t, $NIL) = $CONS (ONE t, $NIL)
| insTree (t, $CONS (ZERO, ds)) = $CONS (ONE t, ds)
| insTree (t, $CONS (ONE t', ds)) =
$CONS (ZERO, insTree (link (t, t'), ds)) (* 全ての関数節が再帰無しに遅延されるようになった *)差異はinsTree関数呼び出し時にdsにパターンマッチ(force)するかどうかだけ:
- dsは一つ前のinsTree呼び出しの結果(r0だったもの)
- そしてr0には必ず二回
execが適用されているので、先頭要素が既にforce済みであることは確実 - そのためここで先頭要素にパターンマッチ(force)しても評価が始まることはないので、実行コストには影響を与えない
! 以降は本筋とはあまり関係がないので、省略予定 (時間に余裕がありそうなら含める)
insert以外の関数を新しいデータ構造に合わせて修正するのは難しくない。
四つの有用なコメントを書いておく:
-
mergeとdeleteMinは全てのサスペンションを評価している
-
- 定理7.1からヒープは最大で
O(log n)個の未評価サスペンションしか保持していない
- そのため全てのサスペンションを評価しても
merge,findMin,deleteMinの最悪コストのオーダは変わらない
- 定理7.1からヒープは最大で
-
removeMinTreeは時々ZEROで終わるストリームを生成するが、以下のいずれかなので問題ない:
findMinによって捨てられるdeleteMin内で全要素がONEのリストによってマージされる
-
deleteMinは以前よりも仕事している
- 子供のリストを有効なヒープに変換する仕事が増えた
listToStream (map ONE (rev children))
問: 特定用途向けの最適化されたmrg関数(mrgWithList)を実装せよ。
mrgWithList(rev c, ds') = mrg (listToStream (map ONE (rev c)), ds')
fun mrgWithList(cs, $NIL) = listToStream(map ONE cs)
| mrgWithList([], ds) = ds
| mrgWithList((c :: cs), $CONS(ZERO, ds)) = $CONS(c, mrgWithList(cs, ds))
| mrgWithList((c :: cs), $CONS(ONE t, ds)) =
$CONS(ZERO, insTree (link(c, t), mrgWithList(cs, ds)))目的:
- 6.4.3のマージソートのコストを償却から最悪に変換する
- add関数:
O(log n) - sort関数:
O(n)
- add関数:
add関数:
- もともとはaddSeg関数だけがモノリシックな遅延評価関数だった (全体で)
- インクリメンタルにする必要がある
- ただし
mrgだけをインクリメンタルすれば十分 mrgを除けば、addSegはO(log n)ステップなので、正格に実行するだけ要求を満たせる
- ただし
mrgfun lazyを付与 + 対象をstreamにすることでインクリメンタル(各ステップをO(1))に実行可能にしたsort実行時に未評価サスペンションがO(n)に収まるように、addの各呼び出しでスケジュールを実行する必要がある
sort関数:
- ソート自体のunshared-costは(以前と変わらず)
O(n)- 今回は最後に
streamToListの呼び出しが増えたが、それもO(n)
- 今回は最後に
- shared-costに関しては、add関数が適切にスケジュールを実行してくれれば
O(n)に収まる
セグメントの表現は変更する:
listからstreamに変更- また各セグメントにスケジュールを持たせる
- 償却解析では、
addの償却コストはおおよそ2B'であったB'は、n' = n + 1内の1bitの数- つまり、セグメント(数値表現なら1bit)毎に二つのサスペンションを実行すれば良い
- セグメントの型は
Elem.T Stream list - 各ストリームは遅延された
mrg呼び出しに対応する
- 償却解析では、
最終的なデータ型定義とスケジュール実行関数:
(* データ型定義 *)
type Schedule = Elem.T Stream list
type Sortable = int x (Elem.T Stream x Schedule) list
(* スケジュール実行: mrg関数の遅延された各ステップを実行する *)
fun exec1 [] = []
| exec1 (($NIL) :: sched) = exec1 sched (* ストリーム一つ分のマージが完了した *)
| exec1 (($CONS (x, xs)) :: sched) = xs :: sched
(* exec1関数を二回呼び出すだけ *)
(* add関数は、exec2関数を、各セグメントに対して呼び出す *)
fun exec2 (xs, sched) = (xs, exec1 (exec1 sched))add関数の定義:
(* add関数: 基本的な処理の流れは以前と同様 *)
fun add (x, (size, segs)) =
let fun addSet (xs, segs, size, rsched) =
if size mod 2 = 0 then (xs, rev rsched) :: segs (* マージ時の依存関係を考慮してスケジュールは要素数が少ないストリーム順にスケジュールに格納する *)
else let val ((xs', []) :: segs') = segs (* []は未評価の古いセグメントが残っていないことのアサート *)
val xs'' = mrg (xs, xs') (* mrgはインクリメンタル *)
in addSet (xs'', segs', size div 2, xs'' :: rsched) end
val segs' = addSeg ($CONS (x, $NIL), segs, size, []) (* addSegは正格になった *)
in (size+1, map exec2 segs') end (* 各セグメントにexec2を適用 *)- add関数のunshared-costは
O(log n)- =>
O(log n)回のexec2呼び出しがO(1)で終わることが証明できればOK
- =>
- sort関数のunshared-costは
O(n)- => 未評価のサスペンションが
O(n)であることが証明できればOK
- => 未評価のサスペンションが
マージの各ステップは他の二つのストリームに依存している:
- 現在のストリームは
S'[i] - 依存のストリームは
S'[i-1]とS[i]S'[i] = merge(S'[i-1], S[i])
S'[i-1]は、S'[i]の前にスケジュールされているので、S'[i]の実行前に完全に評価されているS[i]は、S'[i]を生成するadd呼び出しの前に、完全に評価されているはず- 補助定理 7.2で証明
- 上の二つにより、
exec2の各呼び出しの最悪コストはO(1)
サイズnの任意のソート可能コレクションに関しては、サイズが
m=2^kのセグメント用のスケジュールは、最大で2*m - 2*(n mod m + 1)要素を含んでいる
この補助定理により、次の二つが成立する:
addSegでのマージ対象となるストリームは全て完全に評価済みである- 全体の未評価サスペンションは最大でも
O(n)である
2*m - 2*(n mod m + 1)に関する補足:
- 最大値: (数値表現で)下位kビットが全て0
- セグメントができた直後
2*m - 2
- 最小値: (数値表現で)下位kビットが全て1
- セグメントがマージされる直前 (後一つでも要素が増えたらマージされる)
2*m - 2*m = 0
状況:
- サイズnのソート可能コレクション
- nの下位kビットが1
- nは
c * 2^(k+1) + (2^k - 1)と書ける (cは適切な整数値)
- nは
addはサイズがm = 2^kの新しいセグメントを生産する (! 新セグメントができたケース)- スケジュールは
2,4,8,...,2^kのストリーム群を含んでいる - スケジュールの合計サイズは
2^(k+1) - 2 = 2*m - 2 exec2実行後に、スケジュールのサイズは2*m - 4になる- 新しいコレクションのサイズは
n' = n + 1 = c*2^(k+1) + 2^k 2*m - 4 < 2*m - 2*(n' mod m + 1) = 2*m - 2なので、このセグメント関しては補助定理が成立する
- スケジュールは
- mより大きいサイズm'のセグメントは、原則
addによる影響は受けない (! 小さいセグメントへの要素追加があったケース)exec2の実行だけは例外- スケジュールのサイズが2減る
- 新しい上界:
2*m' - 2*(n mod m' + 1) - 2 = 2*m' - 2*(n' mod m' + 1) - => 条件を満たしている
- 新しい上界:
- nの下位kビットが1だとする (! セグメントがマージされたケース)
m = 2^i where i < kが成り立つ任意のセグメントに関して、スケジュール内の要素数は最大でも、2*m - 2*(n mod m + 1) = 2*m - 2*((m - 1) + 1) = 0- 完全に評価済み
コレクション内のスケジュール群の要素数合計は最大でも:
- 式は本を参照
- 直感的には、セグメント作成後に要素が追加(1bit部分)が追加される度にスケジュールは減っていくので、一番最上位のセグメントの生成直後が最も要素数が多い (きっと...)
- 上限: 2n
- => sort関数の最悪コストは
O(n)
- 6.4.3の物理学者の手法のポテンシャル関数に似てるね
省略