minglejingle.md

Minglejingle: Scalable blockchain with non-interactive transactions

This article describes the Minglejingle (MJ) protocol: a redesign of Mimblewimble (MW) for non-interactive transactions. It preserves the security and privacy properties, supports payment proofs, non-interactive coinjoin and secure pruning of spent outputs.

1. Introduction

Blockchains are distributed ledgers that preserve the transaction history so that new network participants can, at any point in the future, verify these two security properties:

1. Supply security: No counterfeit coins have been created.
2. Ownership security: No coins have been moved without the authorization by the owner of the associated private keys.

Bitcoin achieves unconditional supply security as a result of transparent transaction amounts. Ownership security is achieved by storing all historical transactions forever, which allows the signatures authorizing the transfer of coins to be verified at any time.

The Mimblewimble protocol, proposed in 2016 by an anonymous researcher [1], makes blockchains much more efficient, while still providing both of the security properties. MW replaces output values with homomorphic Pedersen commitments, which allows both the supply security and the ownership security to simplify to a single signature verification per transaction while removing the need to keep all historical ouputs in the blockchain.

However, the efficiency and elegance of MW comes at a cost. All transactions must be constructed interactively by the sender and all the receivers. This has both usability and security implications:

1. The sender and the receivers must typically be online at the same time and be able to communicate. Since most users connected to the Internet don't have a public IP address, the interaction is usually done via Tor or using a third party service.
2. The private keys are needed in order to receive funds. This means that the recipient must typically keep their private keys in a hot wallet connected to the internet. This poses an additional security risk.

There have been many proposals how to alleviate these issues and enable non-interactive/one-sided transactons in the MW protocol. However, these proposals either don't support payment proofs [2] or don't provide ownership security [3, 4, 5].

1.1 Contribution

This article presents Minglejingle, a redesign of the MW protocol with the following features:

1. Transactions are fully non-interactive. The sender only needs to know the recipient's address, which consists of 2 public keys.
2. Addresses are not linkable to wallets.
3. Transactions outputs are not linkable to addresses.
4. Blocks don't link transaction inputs to outputs.
5. The protocol provides both supply security and ownership security.
6. Prunable data from spent outputs are not needed for chain verification.
7. The protocol provides unconditional payment proofs.

As MJ represents a compromise between efficiency and usability, there are some drawbacks:

8. The protocol requires more complex consensus rules than MW.
9. The amount of data that new nodes need to download in order to verify the full transaction history is 2-4 times larger than in MW, depending on the fraction of spent outputs. However, this is still several times less than other non-interactive protocols with similar privacy properties (details in §7.1).

2. Cryptographic primitives

2.1 Notation

We assume that 𝔾 is a cyclic group of prime order q ≈ 22*λ, where λ is the security level in bits. Uppercase letters usually refer to group elements (public keys, commitments) and lowercase letters usually refer to numbers in Zq (scalars, private keys). We will use the additive notation for group operations.

Let G be the generator of 𝔾 and H be another element of 𝔾 with unknown discrete logarithm relationship to G.

2.2 Hash functions

We assume the existence of the following hash functions:

• Hb is a hash function {0,1}* -> {0,1}b. For preimage resistance, b = λ. For collision resistance, b = 2*λ.
• Hq is a hash function {0,1}* -> Zq

These hash functions are modeled as random oracles with uniform outputs over their domains.

2.2.1 Tagging

Tags are used to prevent the outputs of hash functions from being misused in a different context than intended. Tags will be denoted by capital letter T with a lower index specifying the name of the tag. Tags are passed to hash functions alongside other input fields. For example, Tsend is a tag specifies that the input is used in the context of sending funds.

2.3 Pedersen commitments

Pedersen commitment C is an element of 𝔾 constructed as:

C = r * G + v * H

where r is the blinding factor and v is the value of the commitment. Pedersen commitments are homomorphic, which means that adding two commitments C1 and C2 to values v1 and v2 produces a commitment to (v1 + v2) mod q

2.4 Range proofs

When adding Pedersen commitments, their values are added modulo q. To prevent overflow, we need to restrict the possible values of v to a range much smaller than q. Range proofs are a special kind of zero-knowledge proofs that prove a commitment C is of the form r*G + v*H where 0 <= v < 2n and n is the required precision in bits, without revealing the values r or v. For monetary operations, 64-bit precision is more than enough to represent the possible range of values.

This article assumes the use of Bulletproofs++, a short and efficient range proof that requires 10 group elements and 3 scalars to prove that v is a 64-bit value. [6]. The proofs for several different commitments can be aggregated with a logarithmic increase in proof size.

2.5 Diffie-Hellman key exchange

If Alice owns a keypair (xa, Pa) and Bob owns a key pair (xb, Pb), then xa* Pb = xb* Pa is a secret that only Alice and Bob can compute after sharing their public keys Pa and Pb. This is called the Diffie-Helmann (DH) key exchange protocol. [7]

2.6 Schnorr signatures

Schnorr signatures are a family of digital signatures based on the discrete logarithm problem (DLP). We consider 3 variants of the signature scheme with different sizes and features. All variants provide λ bits of security against forgery.

signature	size	batch	adaptor	security proof
Standard Schnorr	4*λ	✓	✓	GGM+ROM [8]
Short Schnorr	3*λ		✓	GGM+ROM [9]
Half-aggregated Schnorr	2*λ	✓		AGM+ROM [10]

• batch = supports batch verification (several signatures can be verified with a single multiexponentiation operation)

• adaptor = supports adaptor signatures ("scriptless scripts")

2.6.1 Standard Schnorr

To sign a message m using the private key x (corresponding to the public key P), the signer selects a random nonce value r and calculates R = r*G. The signature then consists of the pair (R,s), where s = r + e*x with e = Hq(R, P, m).

A signature (R,s) of the message m can be verified with the public key P by checking s*G ?= R + Hq(R, P, m)*P.

2.6.2 Short Schnorr

To sign a message m using the private key x (corresponding to the public key P), the signer selects a random nonce value r and calculates R = r*G. The signature then consists of the pair (e,s), where s = r - e*x and e = Hλ(R, P, m).

A signature (e,s) of the message m can be verified with the public key P by checking e ?= Hλ(e*P + s*G, P, m).

2.6.3 Half-aggregated Schnorr

Given N standard Schnorr signatures σ1 = (R1, s1), σ2 = (R2, s2), ..., σN = (RN, sN) for public key-message pairs (P1, m1), (P2, m2), ..., (PN, mN), they can be aggregated into a single signature σaggN = (R1, R2, ..., RN, sagg) of size 2*λ*(N+1) bits.

This aggregation does not require interaction with the original signers and can be done incrementally, i.e. given σaggN and a new signature σN+1, it is possible to calculate σaggN+1 (IASchnorr scheme in [10]). This has advantages for blockchain applications, allowing miners to collect transactions and incrementally aggregate them into a block.

It should be noted that the security proof for Half Schnorr requires a slightly stronger assumption (the algebraic group model) compared to Standard and Short Schnorr, which have been proven in the generic group model. However, this assumption seems sensible for practical use with elliptic-curve groups.

2.6.4 Interactive multi-signatures

Standard Schnorr signatures of the same message with two or more private keys can be aggregated into one multi-signature (R,s) if the signers cooperate. This interactive protocol is described in §3.2.2 as part of the MW protocol.

2.7 Elliptic curve choice

For the 128-bit security level, a good choice to represent the group 𝔾 is the ed25519 elliptic curve. It is a twisted Edwards curve that has complete point addition formulas, allowing fast and secure constant-time implementations. Although this curve has a cofactor of 8, this can be eliminated by using the Ristretto abstraction for group elements, which produces a prime-order group and protects from small-subgroup attacks [11].

2.7.1 Sizes

The table below lists the serialized sizes of the cryptographic primitives when using the ed25519 elliptic curve.

primitive	elements	size (bytes)
private key, scalar	Zq	32
public key, commitment	𝔾	32
range proof (BP++)	10x 𝔾, 3x Zq	416
2x aggregated BP++	10x 𝔾, 5x Zq	480
Standard Schnorr	1x 𝔾, 1x Zq	64
Short Schnorr	1.5x Zq	48
Half-aggregated Schnorr	1x 𝔾	32

3. Baseline protocols

3.1 Bitcoin with CT (BCT)

For comparison, we show what a simplified Bitcoin protocol might look like with Confidential Transactions (CT), i.e. output amounts hidden with Pedersen commitments.

3.1.1 Transaction inputs

In order to spend an output, the sender must add the following data to the blockchain:

• The ID of the transaction and the index of the output that's being spent
• A Schnorr signature (R, s) showing the possesion of the private key for the output
• The difference d between the blinding factors of the outputs and the blinding factors of the inputs.

If multiple inputs are spent at once, the signatures become multi-signatures (§2.6.4), so two inputs require 168 bytes of data.

3.1.2 Transaction outputs

The following data needs to be stored in the BCT blockchain for each output:

• The output commitment C = r*G + v*H
• A range proof showing that 0 <= v < 264
• The receiver's public key Kr
• The sender's emphemeral public key Ke for DH key exchange
• The value v encrypted with the shared key between the sender and the receiver. The blinding factor r can be derived deterministically from the shared secret.

If multiple outputs are created at once, the range proofs can be aggregated.

3.1.3 Verification

Each BCT transaction can be verified in 2 steps:

1. Checking that the difference between the output commitments and the input commitments is equal to d*G. This proves that the transaction values balance out.
2. Checking that (R, s) is a valid Schnorr multi-signature with the input public keys.

3.1.4 Privacy

The only privacy feature provided by BCT is that the transaction amounts are hidden.

3.1.5 Payment proofs

Since transactions are stored on the blockchain forever, payment proofs are easy. The sender only needs to point to a transaction output and provide the private key for Ke to reveal the value of the output.

3.2 Mimblewimble

Our main baseline is the interactive MW protocol.

3.2.1 Transactions

Each MW transaction consists of:

• One or more inputs, which are just Pedersen commitments and refer to unspent outputs of previous transactions.
• One or more outputs, each consisting of a Pedersen commitment and a range proof.
• A transaction kernel, which consists of a public key K and an associated Schnorr signature (R, s).
• An offset o, which can be aggregated.

3.2.2 Interactive protocol

If Carol, who owns an unspent output Ci = ki*G + vi*H wants to send vo coins to Dave, the following interactive protocol must be executed:

1. Carol calculates the change output value vc = vi - vo, constructs the change output Cc = kc*G + vc*H, selects a nonce rc and offset oc, then sends Ci, Cc, vo, oc and Rc = rc*G to Dave.
2. Dave constructs his output Co = ko*G + vo*H, constructs a range proof for Co, selects a nonce rd and offset od, calculates the kernel public key K = Co + Cc - Ci - (oc + od)*G, calculates the aggregated nonce R = Rc + rd*G and constructs a partial signature sd = rd + (ko-od)*Hq(R,K), then sends Co, the range proof, Rd = rd*G, od and sd back to Carol.
3. Carol completes the signature as s = sd + rc + (kc-ki-oc)*Hq(R,K) and can finally construct the transaction consisting of the input Ci, the outputs Co and Cc with the associated range proofs, the kernel K, kernel signature (R,s) and the offset o = oc + od.

3.2.3 Verification

The resulting transaction can be easily validated by checking:

1. Co + Cc - Ci ?= K + o*G
2. s*G ?= R + K*Hq(R,K)

The signature verification in step 2 serves both as a balance proof (K doesn't contain any coins) and the proof of ownership.

3.2.4 Pruning

The MW protocol allows for the removal of spent outputs and the inputs of all transactions while preserving the security properties. Each historical transaction only leaves behind the kernel, which is about 96 bytes at the 128-bit securit level.

3.2.5 Efficiency analysis

The main points that make MW so efficient are the following:

• The use of the blinding factor to both obscure the values of the outputs and to authorize the spending.
• Unspent outputs consisting of the absolute minimum amount of data (only a commitment + range proof).
• The removal of spent outputs.
• The kernel signature being an aggregated signature over all of the involved private keys.

3.2.6 Privacy

MW is more private than BCT. Since transaction inputs and outputs are only linked indirectly via the kernel public key and the kernel signature doesn't sign any output data, MW provides "accidental" privacy by enabling non-interactive coinjoin.

3.2.7 Payment proof

The MW blockchain doesn't include any provisions for payment proofs. If the Carol requires a payment proof, it must be provided by Dave in step 2 of the interactive protocol. The validity of the payment proof must be bound to the existence of the transaction kernel on the blockchain to resolve disputes in the case Carol doesn't complete step 3 or if Dave spends the output.

4. Towards a non-interactive protocol

4.1 Goals

The main design goals are the following:

1. Fully non-interactive transactions.
2. Both supply security and ownership security .
3. Unconditional payment proofs.
4. Privacy equivalent to the interactive MW protocol.
5. Smallest possible blockchain.
6. Fastest possible verification.

4.2 Simulating the receiver

For Carol to be able to construct a MW-like transaction non-interactively, she must be able to derive all values from step 2 of §3.2.2 that are provided by Dave in the interactive protocol. This can be achieved using the DH key exchange. The shared DH key can be used for the following:

1. Generating the blinding factor rd for Dave's output commitment. The blinding factor must be known to Carol to enable her to construct the required range proofs.
2. Encrypting the value vo and other data associated with the payment.

Observation 1
Because the blinding factor is known by both Carol and Dave, it is no longer sufficient as a proof of ownership of the output.

In order to restrict the ability to spend the output to Dave, the transaction output needs to include an output key that only Dave knows the private key for.

4.3 Balance equation

Since the blinding factors cannot be used to prove output ownership, we can safely drop the kernel commitment K from the balance verification equation §3.2.3.1, which then becomes simply:

Co + Cc - Ci ?= o$*G

This proves that no new coins were created in the transaction and it doesn't require a signature. The offset o$ ensures that coinjoins cannot be undone. This also means that MJ doesn't have transaction kernels and transaction balances are verified the same way as for Bitcoin with CT.

4.4 Addresses

To enable non-interactive transactions, we need to introduce addresses. For privacy reasons, Dave's output received from Carol should be bound to a unique one-time public key that is cryptographically unlinkable to Dave's public address.

Additionally, we want to enable Dave to generate a virtually unlimited number of different unlinkable addresses so that noone can trace his online activities.

We can achieve both of these properties with a variant of the subaddress scheme used by Monero. [12]

4.4.1 Address generation

Dave can generate a pair of private keys a and b (in practice, both keys can be derived from the same secret seed). a is called the private view key and can be used to recognize payments. b is the private spend key and is needed to spend outputs. Separating the viewing and spending ability allows the private view key to be revealed to an auditor without risking a loss of funds.

Whenever Dave needs an address, he can select an integer index i and generate the associated public address (Ai, Bi) as:

m_i = H_q(T_addr, a, i)

A_i = a*(m_i + b)*G

B_i = (m_i + b)*G

Notice that Ai = a*Bi for any index i. This allows Dave to calculate a DH shared secret using the same private key a for all his addresses.

4.4.2 Diffie-Hellman key exchange

Carol can construct a shared secret with Dave based on his public address (A, B) constructed according to §4.4.1 for some index i unknown to Carol.

1. Carol can generate a random scalar s.
2. The secret shared between Carol and Dave is Q = s*A = s*a*(mi + b)*G.
3. Carol will include the ephemeral public key Ke = s*B with the transaction data.
4. Dave can derive the shared secret using his private key a as Q = a*Ke = a*s*(mi + b)*G.

4.4.3 One-time key construction

Using the shared secret Q, Carol can derive a private key x, which will allow her to construct a unique one-time public key for Dave: Ko = x*G + B. Only Dave knows the corresponding private key.

Dave can later recognize the key by calculating B = Ko - x*G.

4.4.4 View tags

To make it faster for Dave to recognize that a particular output key Ko is his, Carol can include a 1-byte value t = H8(Ttag, Q) with the transaction data. This will allow Dave to eliminate 99.6% (=255/256) of non-owned outputs after deriving the shared secret. This idea was first proposed for Monero and can reduce the time to test output ownership by at least 15% [13].

4.5 Ownership security after pruning

To achieve an efficient blockchain, we'd like to prune spent outputs. However, since we don't have transaction kernels, we need to retain some other witness data for each spent output so that:

1. Ownership security can be retrospectively verified.
2. A payment proof can be provided even after the recipient spends the output.

Observation 2
For each spent output, the output key Ko and the associated signature must be kept in the blockchain forever.

It would be nice to save blockchain space and include just one multi-signature for all the spent output keys in each transaction. Unfortunately, this is not possible to do securely without explicitly linking inputs together (and thus revealing common input ownership). Since any of the Ko values may be rogue keys, the keys and signatures would have to be aggregated in a way that commits to all of the keys in advance. The reader should refer to the Bellare-Neven multisignature scheme for details [14]. Note that MW doesn't have this problem because the range proofs show that none of the output commitments is a rogue key, but this cannot be done non-interactively.

The best we can do is to keep Ko and a half-aggregated Schnorr signature separately for each transaction input.

However, this still has 2 problems:

1. What message should the inputs sign? We cannot sign the outputs, since that would create an explicit link we want to avoid. If we sign a message independent of the outputs, this makes the transaction malleable and any malicious network participant can swap the transaction outputs for their own.
2. How can future verifiers be convinced that the key Ko in the list of spent outputs is indeed the key that was in the pruned output?

This leads to the following observations:

Observation 3
The signatures with the input keys Ko must be cryptographically bound to the newly created outputs.

The solution is two-fold:

1. The sender must sign each output with an ad-hoc key ks and include Ks = ks*G with the output data. This ensures that the output data cannot be tampered with.
2. If the nonce of the half-Schnorr signature of a transaction input is Ro, the sender must provide a scalar o# such that: ΣTXIN Ro + ΣTXOUT Ks = o#*G. This homomorphically binds the inputs to the outputs in a similar way to MW.

Observation 4
To enable pruning, the signatures with the input keys Ko must be verifiable without access to the pruned data.

The way to solve this problem is to split the output data into two parts: unprunable data to be kept in the blockchain forever and prunable data not needed for future verification. The prunable data will be linked to the output by a signed hash.

5. Protocol description

5.1 Transaction outputs

Each MJ transaction output consists of prunable data (PD) and unprunable data (UD).

The prunable data has fields that are no longer needed if the output is spent:

field	description	size
Co	amount commitment	32
RP	range proof for Co	416
Ke	key exchange public key	32
t	view tag	1
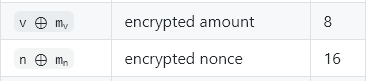
v	amount	0/8 (hidden in the range proof)
n	nonce	0/16 (hidden in the range proof)
	total	481

The unprunable data has fields necessary for future blockchain verifiers:

field	description	size
Ks	sender public key	32
PID	prunable ID	16
Ko	one-time output key	32
σs	short Schnorr signature	48
	total	128

The total size of each output is 609 bytes.

5.1.1 Output construction

Let's suppose that Carol and Dave have agreed in advance on an amount v to be sent and Dave has provided his public address (A, B).

1. Carol can begin constructing the output for Dave by selecting a 128-bit nonce n uniformly at random. We will later explain how this nonce can be used for payment proof.
2. Carol calculates a unique sending key s = Hq(Tsend, A, B, v, n)
3. Carol calculates the DH exchange public key as Ke = s*B.
4. Carol derives a DH shared secret as Q = s*A.
5. Carol calculates the view-tag t = H8(Ttag, Q).
6. Carol derives a shared secret key u = H256(Tderive, Q)
7. Carol feeds the shared key u into a stream cipher to derive a key extension x, a blinding factor c and the secret scalars needed for the range proof.
8. Carol constructs a one-time public key for Dave: Ko = x*G + B.
9. Carol calculates the amount commitment Co = c*G + v*H.
10. Carol constructs a range proof RP for Co in such a way that Dave can later replay the proof to recover the output amount v and the nonce n from the proof data.
11. Carol calculates PID = H128(Tprunable, PD)
12. Carol generates a private key ks uniformly at random and derives a unique sender public key Ks = ks*G.
13. Carol signs the tuple (PID, Ko) using her private key ks. The result is a short Schnorr signature (es, ss).

5.1.2 Output recognition

Dave can do the following for each unspent output in the blockchain:

1. Derive the nominal shared secret Q' = a*Ke.
2. Derive the nominal view tag t' = H8(Ttag, Q')
3. If t != t', this output is not owned by Dave.
4. Derive a shared key u = H256(Tderive, Q).
5. Dave feeds the shared key u into a stream cipher to derive a key extension x, a blinding factor c and the secret scalars needed for the range proof.
6. Calculate the nominal spend key B = Ko - x*G
7. If B is not equal to any of Dave's generated spend keys, this output is not his.
8. Replay the range proof to recover the amount v and nonce n.
9. Check that Co ?= c*G + v*H
10. Look up the public view key A associated with B.
11. Calculate Carol's sending key: s = Hq(Tsend, A, B, v, n)
12. Check that s*B ?= Ke

Note that none of these steps requires the private spend key b, so they can be done by an auditor on behalf of Dave. 99.6% of non-owned outputs will abort early in step 3 thanks to the view tag. Steps 11-12 are needed in order to prevent the Janus attack that can be used to link addresses that have the same private view key [15]. If the final check fails, Dave should not confirm the receipt of the payment and should not spend the output.

5.2 Tranaction inputs

Each transaction input consists of the following two fields:

field	description	size
OID	previous output ID	32
Ro	Half-aggregated Schnorr signature	32
	total	64

To spend a previously received output with an output key Ko, Dave must provide OID = H256(Toutput, UD) as the ID of the output being spent and a signature (Ro, so) of the empty string that can be verified with Ko, i.e.:

1. Generating a random nonce ro and calculating Ro = ro*G
2. Calculating a challenge e = Hq(Tschnorr, Ro, Ko)
3. Calculating so = ro + e * ko

We can notice that besides authenticating Dave as the legitimate owner of the spent output, each input signature also implies that Dave knows the private key of Ro.

The signature field so can be aggregated by miners for all inputs spent in the block (see §2.6.3).

5.3 Transaction offsets

After constructing one or more outputs according to §5.1.1, Dave can complete the transaction by calculating the two transaction offsets:

o$ = ΣTXOUT cj - ΣTXIN cj

o# = ΣTXIN roj + ΣTXOUT ksj

Here TXIN is a sum over the transaction inputs, TXOUT the sum over the transaction outputs, c are the amount blinding factors, ro the input signature nonces and ks the sender private keys.

When two or more transactions are non-interactively aggregated, the offsets o$ and o# are added together and it's no longer possible to reverse the aggregation to find out which inputs belong to which outputs.

5.3 Minglejingle transaction

An MJ transaction consists of:

• One or more inputs. The input format is described in §5.2.
• One or more outputs. The output format is described in §5.1.
• Two offsets o$ and o# described in §5.3.
• The values of so for each input.

The scalars o$, o# and so can be aggregated for the whole block, so the size of a 2-in 2-out transaction is 1346 bytes. A spent transaction will leave 384 bytes in the blockchain (64 bytes per input and 128 bytes per output).

5.4 Validation rules

In order to verify the whole transaction history, a node needs:

• All block headers.
• The total money supply μ. This can be implicit from the block height or derived from the block headers.
• The list of all input tuples (OID, Ro).
• The list of all unprunable output tuples (Ks, PID, Ko, σs).
• Prunable data of all unspent outputs.

Compared to Bitcoin, prunable data is not needed for validation.

The six validation rules are the following:

1. The aggregated signature soagg in each block is valid for all the spent inputs in that block.
2. The signatures σs are valid for all outputs.
3. The supply balance holds: ΣUTXO Coj ?= μ*H + o$*G
4. The input-output balance holds: ΣTXIN Roj + ΣTXOUT Ksj ?= o#*G
5. All unspent outputs have valid range proofs.
6. The PID of all unspent outputs matches the prunable data.

Similar rules apply for mempool transaction validation except the input signatures are not aggregated yet and the μ*H term is replaced with the sum of the spent input commitments ΣTXIN Coj.

5.5 Payment proof

To prove that she sent money to Dave, Carol can provide an arbiter with:

• Dave's address (A, B)
• The transaction amount v
• The one-time nonce n

The arbiter can verify Carol's claim by:

1. Calculating the sending key s = Hq(Tsend, A, B, v, n)
2. Deriving the shared secret u = H256(Tderive, s*A).
3. Deriving the key extension x from u.
4. Constructing the corresponding one-time public key for Dave: Ko = x*G + B

The arbiter can then check if an input or an output exists in the blockchain with the key Ko.

5.5.1 A spent input exists

If a spent input exists with this key, the arbiter is convinced that the payment has taken place. Dave's signature with the key Ko indisputably proves that Carol's output was correctly formed.

5.5.2 An unspent output exists

If an unspent output exists with the output key Ko, additional checks are needed to ensure that the prunable data is correctly formed. The arbiter can follow the output construction procedure from §5.1.1 and validate the output. If the output is malformed (e.g. the amount commitment doesn't have the correct value, the view tag or the hidden nonce are invalid etc.), blame can be assigned to Carol.

6. Security analysis

6.1 Linking addresses to a wallet

Given two addresses (Ai, Bi), (Aj, Bj) generated according to §4.4.1, deciding whether they belong to the same wallet requires solving the decisional Diffie-Hellman problem in 𝔾 [16]. This problem is considered intractable if the used elliptic curve has a large embedding degree, as is the case for most non-pairing-friendly curves such as ed25519.

An active attack may be attempted by Mallory if she suspects that (Ai, Bi), (Aj, Bj) are both owned by Dave. This requires her to deviate from the output construction process described in §4.3.2 by calculating the shared secret as u = H256(Tderive, s*Ai), setting the key exchange public key to Ke=s*Bi and the output key to Ko = x*G + Bj. However, Mallory won't be able to provide a nonce value n that passes the check in step 12 of §5.1.2, so Dave will be able to detect this attack and won't confirm the payment to Mallory. Mallory will not be able to provide a payment proof because in fact, she created an invalid output to address (Ai, Bj).

6.2 Linking outputs to an address

Linking an output to an address requires either solving the discrete logarithm problem by calculating the receiver's private view key a or by guessing the sender's nonce value n (assuming the amount is known to the attacker). Both of these problems are intractable.

6.3 Breaking supply security

There are two approaches to breaking the balance equation §5.4.3:

1. Calculating the discrete logarithm of the generator H.
2. Creating a valid range proof for a negative value.

The first approach requires solving the DLP in 𝔾, which is intractable. The second approach is intractable if the range proof is sound.

6.4 Breaking ownership security

Stealing an unspent output with N confirmations requires either forging a signature with the output key Ko or a chain reorganization at least N blocks deep (assuming the attacker is the original sender).

Stealing an unconfirmed output requires the knowledge of the private key ks, so it can only be done by the original sender (this is called a double-spend attack).

These are the same security properties that Bitcoin has.

6.5 Replay attacks

MJ is susceptible to the following replay attack:

1. Mallory sends an output (OID1, Ko1) to Dave.
2. Some time later, Dave spends the output in transaction TX2.
3. Mallory again sends an identical output (OID1, Ko1) to Dave. This requires Mallory to use the same sender nonce and amount as before.
4. Anyone can replay the transaction TX2 to spend this output the same way Dave spent the first copy of the output.

A similar attack applies to Mimblewimble [17]. Solving this attack may not require consensus changes because Dave will be able to detect the duplicate output and won't provide any goods or services to Mallory for the payment. If Mallory tries to dispute the payment, the arbiter will clearly see the duplicate output keys in the blockchain, which can only occur in one of two cases (besides a negligible chance of a collision):

1. Mallory deliberately sent the duplicate payment.
2. Mallory is a victim of a longer chain of replayed transactions.

In the first case, the fault lies with Mallory. In the second case, someone else caused the replay attack, in which case Mallory actually didn't make the payment. In both cases, the arbiter may conclude that Dave is not obligated to provide any goods or services to Mallory.

6.6 Forging payment proofs

Given an output key Ko in the blockchain, Mallory can try to forge a payment proof with a value of v to the address (A,B):

1. If Mallory knows the private keys for Ko and B, she can forge the proof by calculating x = ko - b, inverting the stream cipher to calculate u, calculating a hash preimage to get the shared secret Q, solving for the discrete logarithm of the Diffie-Hellman point with respect to A and finally, the last hash preimage to get the sending nonce n.
2. If Mallory doesn't know the private key for Ko or B, forging the proof additionally requires the calculation of the discrete logarithm of Ko - B.

In both cases, forging the proof involves solving intractable problems.

7. Efficiency and usability analysis

7.1 Initial blockchain download size

The table below lists the initial blockchain download (IBD) size of MJ in comparison with other protocols at the 128-bit security level. This comparison assumes a blockchain with 750 million transactions with 2 inputs and 2 outputs each and 85 million unspent transaction outputs. For simplicity, we only count bare transaction sizes without block headers, transaction headers, explicit fees, lock times and aggregatable fields.

protocol	2-2 TX size	STXO size	IBD size (GB)	IBD size (visual)
Mimblewimble	1056	-480	110	*
Bitcoin	280		210	**
Minglejingle	1346	-481	329	***
Bitcoin with CT	824		618	******
Monero	2000		1500	**************

7.2 Verification performance

The following table lists the number of Schnorr signatures and BP++ range proofs (in millions) that need to be verified for full IBD validation. Note that performance-wise, a range proof verification is equivalent to about 100 signatures. Protocols are ordered in ascending order of computational requirements.

protocol	signatures	rangeproofs	total CPU (visual)
Bitcoin	750	0	*
Bitcoin with CT	750	<851	**********
Mimblewimble	750	85	************
Minglejingle	3000	85	****************
Monero	900002	750	***************************************************...*************

¹ Range proofs are aggregated and it's only necessary to verify the range proof of transactions with at least one unspent output.

² Assuming CLSAG with a ring size of 16 counting as 60 Schnorr signatures based on available benchmarks.

7.3 Usability and privacy

protocol	NITX	NICJ	CT	BLINK	TLINK
Bitcoin	✓
Mimblewimble		✓	✓	✓
Minglejingle	✓	✓	✓	✓
Bitcoin with CT	✓		✓
Monero	✓		✓	✓	✓

• NITX: non-interactive transactions
• NICJ: non-interactive coinjoin
• CT: hidden transaction amounts
• BLINK: blocks don't link inputs to outputs
• TLINK: transactions don't link inputs to outputs

References

[1] Mimblewimble: https://github.com/mimblewimble/docs/wiki/MimbleWimble-Origin

[2] MW one-sided transactions: https://github.com/mimblewimble/grin-rfcs/blob/a2d9f25cdccf29904ef241df5b608ca3fd16ed61/text/0000-onesided.md

[3] One-sided transactions in MW: https://github.com/DavidBurkett/lips/blob/master/lip-0004.mediawiki

[4] MW non-interactive transactions: https://eprint.iacr.org/2020/1064

[5] Tari one-sided payment: https://rfc.tari.com/RFC-0201_TariScript.html#one-sided-payment

[6] Bulletproofs++: https://eprint.iacr.org/2022/510.pdf

[7] Diffie-Hellman: https://www.cs.utexas.edu/~shmat/courses/cs380s/dh.pdf

[8] Schnorr signatures: https://eprint.iacr.org/2012/029.pdf

[9] Short Schnorr signatures: https://eprint.iacr.org/2019/1105.pdf

[10] Half-Aggregation of Schnorr Signatures: https://eprint.iacr.org/2022/222.pdf

[11] Ristretto: https://ristretto.group/what_is_ristretto.html

[12] Monero subaddresses: https://monerodocs.org/public-address/subaddress/

[13] Monero view tags: monero-project/research-lab#73

[14] Multisignatures: https://cseweb.ucsd.edu/~mihir/papers/multisignatures-ccs.pdf

[15] Janus attack: https://web.getmonero.org/2019/10/18/subaddress-janus.html

[16] Decisional Diffie-Hellman: https://en.wikipedia.org/wiki/Decisional_Diffie%E2%80%93Hellman_assumption

[17] Grin replay attack: https://forum.grin.mw/t/enforcing-that-all-kernels-are-different-at-consensus-level/7368

Commitments and public keys are usually represented with 33 bytes, not 32.

That's true for the secp256k1 curve used by bitcoin. It uses a 256-bit field, so 257 bits are need to store a compressed point (256 bits for the x coordinate and 1-bit parity of the y coordinate). That requires 33 bytes as you mentioned.

However, the ed25519 elliptic curve uses a 255-bit field, so compressed points fit into 256 bits. See for example: RFC 8032.

You're right, I forgot we were dealing in ed25519. False alarm :)

In section 4.3.2, Carol derives the shared secret by calculating t = Hd(Tderive, s*A). You indicate that Carol should include Ke=s*B in the output. Then in section 4.3.3, for Dave to derive the nominal shared secret, you have: t' = Hd(Tderive, a*Ke).

But that doesn't line up. t' would be Hd(Tderive, a*Ke) == Hd(Tderive, a*s*B), whereas t was Hd(Tderive, s*A) == Hd(Tderive, s*a*G).

t != t', because Hd(Tderive, a*s*B) != Hd(Tderive, s*a*G). So did you mean for the key exchange public key to be Ke=s*G instead?

Thanks for the review.

As per §4.3.1, Dave's address (A,B) consists of the following 2 public keys:

A = a*(mi + b)*G

B = (mi + b)*G


where a, b are Dave's private keys, mi = Hs(Taddr, a, i) and i is the index of the address in Dave's wallet.

Note that Carol doesn't know the values of i, mi, a*G or b*G. This is the trick that makes different Dave's addresses unlinkable to him off-chain, which is the same property that Mimblewimble has due to not having addresses. Dave can use the private view key a to recognize payments for all his addresses.

So the shared secret calculated by Carol is s*A = s*a*(mi + b)*G and Dave calculates a*Ke = a*s*B = a*s*(mi + b)*G. These elements are equal.

Do you plan to do a reference implementation?

Do you plan to do a reference implementation?

The protocol needs to be peer-reviewed first. But I think anyone should be able to implement it based on the specification.

As per §4.3.1, Dave's address (A,B) consists of the following 2 public keys:

A = a*(mi + b)*G
B = (mi + b)*G

Indeed it does. I'm sorry, I was skipping around a bit when reviewing, and made faulty assumptions about what A and B were (I assumed each were just a public key generated from the seed with no other relationship between the two).

This is actually really clever since it eliminates the need to check all outputs once for each stealth address you've used. Is this how Monero implements stealth addresses?

Is this how Monero implements stealth addresses?

Yes. Monero calls them "subaddresses" (they start with 8 in base58) and they are used together with the standard "main" address (a*G, b*G), which starts with 4 in base58. However, Monero's implementation is vulnerable to the Janus attack (ref. 11), so using subaddresses may affect privacy in some situations.

The difference is that Minglejingle is not vulnerable to the Janus attack and it doesn't use the "main" address (a*G, b*G) at all, which simplifies the implementation (avoids having to signal to the sender whether to use G or B as the base point for the key exchange) and is also better for UX (only one address type).

A nice write-up! 👍 Here

Here is part of my comments/questions :-)

• In "6.1 Initial blockchain download size", you count a 2-2 TX size of MW as 1376, and MJ as 1714.
  But actually a MW 2-2 TX at least has: 2*33+2*(33+675)+105=1587 bytes, and plus 32 bytes if counting the offset, and plus 3*8=24 bytes if counting the vector size field, and plus several additional bytes if counting some type flags. How do you count this 1376?

• And for your MJ, if I understand correctly, you add Z(33 bytes) in Kernel, add K(33 bytes) in each Output, add signature(64 bytes) in each Input, add K(33 bytes) (duplicated to spending Output K) in each Input, and add O_z (32 bytes) for each transaction. So, a 2-2 TX in MJ add total 33+2*(64+33)+2*33 = 293 bytes, plus 32 bytes if counting the additional offset O_z. How do you count the 1714? (1714-1376=338).

• And regarding the "A spent transaction will leave 320 bytes in the blockchain (128 bytes for the kernel and 96 bytes per input)." in "4.5 Minglejingle transaction", 128 looks missing the count of transaction fee element?

• About the "2.6.4 Non-interactive half-aggregation" and "The two offsets and the values of s_i can be aggregated for the whole block", Does the "half-aggregation" and the "aggregation" have the same security assumption? It's appreciated to give the reference if the half-aggregation has the related paper or proofs.

• About the STXO size. You list -640 for MW and -697 for MJ. But in my view, it should be 708=33+675 for MW and 33 more for MJ. Could you please clarify these numbers?

Thanks for the comments!

1

In "6.1 Initial blockchain download size", you count a 2-2 TX size of MW as 1376, and MJ as 1714.

1376 for MW consists of 2 inputs (2*32 bytes), 1 kernel (96 bytes) and 2 outputs (2*608 bytes). Note that I'm assuming the use of the ed25519 elliptic curve (see this comment), so group elements are serialized as 32 bytes. For the range proof, I'm assming the use of Bulletproofs+, which require 576 bytes for a single proof (see ref. 5).

As for fees, offsets, flags etc., these are not counted in the IBD calculations as mentioned in §6.1:

For simplicity, we only count bare transaction sizes without block headers, transaction headers, explicit fees, lock times and aggregatable fields.

The reason I'm not counting fees and headers is because the sizes can vary considerably depending on the implementation. For example, Grin currently encodes the transaction fee with 8 bytes in the kernel, but that could be reduced to just 2-4 bytes with a more efficient encoding since the fee value doesn't need to support all possible monetary values. In fact, allowing too many choices for the plaintext fee value can be detrimental for privacy.

In other words, the sizes in this article are the theoretical protocol-level minimums.

2

And for your MJ, if I understand correctly, you add Z(33 bytes) in Kernel, add K(33 bytes) in each Output, add signature(64 bytes) in each Input, add K(33 bytes) (duplicated to spending Output K) in each Input, and add O_z (32 bytes) for each transaction. So, a 2-2 TX in MJ add total 33+2*(64+33)+2*33 = 293 bytes, plus 32 bytes if counting the additional offset O_z. How do you count the 1714? (1714-1376=338).

1714 for MJ consists of 2 inputs (2*96 bytes), 1 kernel (128 bytes) and 2 outputs (2*697 bytes). The output fields are described in §4.3.2, which explains the size of 697 bytes. Offsets are not counted in the IBD size as they can be aggregated per block.

3

And regarding the "A spent transaction will leave 320 bytes in the blockchain (128 bytes for the kernel and 96 bytes per input)." in "4.5 Minglejingle transaction", 128 looks missing the count of transaction fee element?

Fees are excluded from the calculation (explained above). In practice, it would probably be around 330 bytes with fees and the support for time-locked outputs.

4

About the "2.6.4 Non-interactive half-aggregation" and "The two offsets and the values of s_i can be aggregated for the whole block", Does the "half-aggregation" and the "aggregation" have the same security assumption? It's appreciated to give the reference if the half-aggregation has the related paper or proofs.

I couldn't find a formal proof, but it's not a new idea. I'm fairly sure it can be proven secure in the random oracle model.

5

About the STXO size. You list -640 for MW and -697 for MJ. But in my view, it should be 708=33+675 for MW and 33 more for MJ. Could you please clarify these numbers?

640 for MW refers to the removal of the input (32 bytes) and the spent output (608 bytes). For MJ, only the output can be removed at 697 bytes. See above for the explanation of the sizes.

I don't know if bulletproofs+ supports this, but for classic bulletproofs over secp256k1, we have the ability to hide some additional data (about 31 bytes) into the bulletproof[1][2]. Perhaps you could use that to hide the amount and nonce and save these 24 bytes:

Instead of generating the nonce mask and value mask with the stream cipher, you could use the cipher to generate the secret key used to hide the bulletproof data.

[1] https://github.com/mimblewimble/secp256k1-zkp/blob/5b39fbf7f1e16e126404791923511723c4c0876d/include/secp256k1_bulletproofs.h#L181
[2] https://github.com/mimblewimble/secp256k1-zkp/blob/5b39fbf7f1e16e126404791923511723c4c0876d/include/secp256k1_bulletproofs.h#L134

wow，cool idea。Is there any new development？

Hi Tevador,

It's been a while since the proposal has been posted, sorry to bump this a bit late - I noticed that the homomorphic hash commitments do not correctly bind the outputs to their kernel. The DLP hardness assumption prevents from directly replacing an output of a transaction in isolation, as mentioned in the description, but does not prevent to replace an output by using another transaction that you aggregate together with the original one.

For example, suppose that Alice creates a transaction with 2 outputs Out1 and Out2. As per the consensus, Alice should compute an offset oZ and a curve point Z (committed to the kernel) that verify
Z = Hp(ID1, K1) + Hp(ID2, K2) + oZ*G.
Suppose that Alice broadcasts this (valid) transaction. A miner can now steal any of the two above outputs, say Out2, by doing the following steps:

1. The miner creates a new transaction that generates a new output Out3 (of their ownership) and chooses some offset oZ'. However, instead of computing the curve point Z'of the kernel with the formula
   Z' = Hp(ID3, K3) + oZ'*G,
   (as it would be expected from an honest user), the miner rather uses the relation
   Z' = Hp(ID3, K3) + Hp(IDM, KM) - Hp(ID2, K2) + oZ'*G,
   where OutM is, similarly to Out3, an output of the miner's ownership (constructed by the miner). OutM should have the same number of coins as Out2.
2. The miner includes in the block Alice's transaction along with their transaction but replaces Out2 with OutM (in particular, Out2 is not included in the block).
3. The miner manages to mine the block.

We see that Z + Z' = Hp(ID1, K1) + Hp(IDM, KM) + Hp(ID3, K3) + (oZ + oZ')*G,
(the two Hp(ID2, K2) cancel out) making the dishonest aggregated transaction (which creates Out1, OutM and Out3) valid and hence the whole block valid, and the miner has in effect stolen the coins that were contained in Out2.

Thanks for reviewing the protocol!

OutM should have the same number of coins as Out2.

The miner would actually need to know the blinding factor of Alice's output commitment. If the blinding factor is not known, the miner would need to copy the commitment and the range proof verbatim from Out2, which can be fixed by signing the output with the range proof (this is not mentioned in the proposal).

Since the blinding factor is shared between the sender and the recipient, this means that when Alice is sending money to Bob, Bob can deny Alice the ability to provide a payment proof by replacing her output Out2 with another output OutBob. This basically makes the output keys KO redundant and degrades the protocol to "Mimblewimble with a shared blinding factor".

Do you think there is a way to fix the protocol while retaining the property that blocks don't link inputs to outputs?

I think it seems hard to fix keeping the idea of the homomorphic hash commitments or similar. You always can cancel out the contribution of an output by replacing it with another one and adjusting the "binding" equation by aggregating another transaction.
You would probably need to also have output binding keys as it is the case for the inputs.

Here is a possible way to fix the protocol:

1. When creating an output, the sender generates a random private key kS, signs the output key KO with it and includes the tuple (kS*G, RS, sS) in the output data. This would increase the size of each output by 96 bytes.
2. The kernel commitment Z would be replaced by a public key KZ = Σ KS + oZ*G, which equals the sum of the sender public keys of the transaction outputs plus the offset. The kernel signature (R, s) would be a proper aggregated signature with both kernel public keys (the sender knows both private keys).
3. Spent outputs would be redefined as tuples (KS, RS, sS, KO, RO, sO), where (RS, sS) is the sender's signature copied from the output and (RO, sO) is the recipient's signature authorizing the spend. Both signatures can be half-aggregated per block, so the asymptotic size per spent output would be 128 bytes (32 bytes more than the original proposal).

The following equation then verifies that no funds have been stolen:

ΣKERN KZ ?= ΣTXI KS + ΣUTXO KS + oZ*G

AFAICS the above attack doesn't apply here because all public keys in this sum must have valid signatures attached to them, proving they are not rogue keys.

This new protocol is slightly less efficient, but I don't see a way to get rid of the double signature for spent outputs without opening rogue key attacks.

The above protocol is vulnerable to an edge-case attack that works as follows:

1. Carol sends an output OutC to Dave. The output is correctly constructed according to the protocol rules.
2. Dave can intercept OutC and collude with a miner to replace it with another output OutD, which contains the same keys KS and KO, but the recipient-only fields are malformed (e.g. the encrypted amount, view tag or the shared secret are wrong). The output otherwise passes all consensus rules.
3. Dave claims that he didn't receive the payment.
4. Carol goes to an arbiter and provides the payment proof.
5. The arbiter reconstructs the output key KO from the payment proof and finds the unspent output OutD in the blockchain. He finds that the output is malformed, assigning blame to Carol.
6. Carol has effectively lost the funds. (Note that Dave cannot spend the output OutD because that would make Carol's payment proof valid).

To fix this problem, the sender must not only sign the output key KO but also a 16-byte hash of the whole output. This hash must then be included for all spent outputs.

The spent-output tuple would become (KS, RS, sS, H16(out), KO, RO, sO), where (RS, sS) = Sign(kS, H16(out) || KO). The asymptotic size per spent output is increased to 144 bytes.

The hash of the output can be truncated to 16 bytes because it only needs to be preimage-resistant (Carol has nothing to gain from constructing two outputs with the same hash). Dave cannot replace OutC with OutD unless H16(OutC) = H16(OutD) (second preimage attack).

I updated the protocol description. The new protocol is slightly less efficient in terms of blockchain size and the number of signatures, but should be secure against the attack described by @kurt256 and is still a lot more efficient than other non-interactive privacy protocols.

Additional changes:

• A more comprehensive description of Schnorr signatures, including security proof references for half-aggregation that were missing in the original write-up.
• Bulletproofs+ replaced with the recently introduced Bulletproofs++, which are much smaller (416 bytes instead of 576 bytes).
• v and n encoded in the range proof as suggested by @DavidBurkett
• Removed transaction kernels, since they are redundant. The balance equation of Minglejingle is therefore simpler than in Mimblewimble.