tkersey/algebra-to-co-monads.md

## algebra-to-co-monads.md

      
                Raw

        
              algebra-to-co-monads.md
            
          
    [fit] Algebra to
[fit] (Co)monads


$$Cᴮᴬ = (Cᴮ)ᴬ$$


$$Cᴮᴬ = (Cᴮ)ᴬ$$


$$Pair&lt;A,B&gt; → C ≅ A → B → C$$


## algebraic-structures.md

      
                Raw

        
              algebraic-structures.md
            
          
    [fit] Algebraic
[fit] Structures

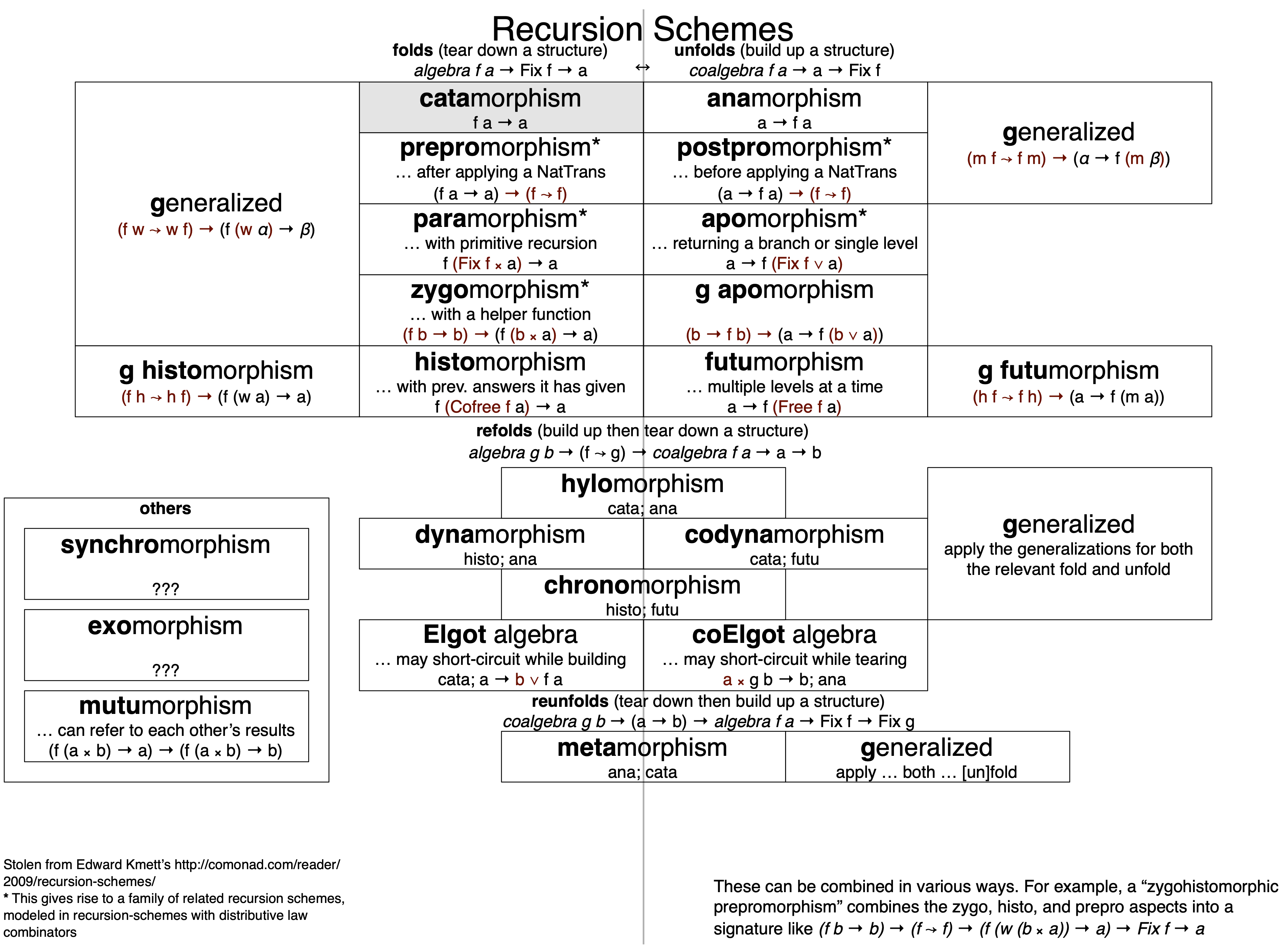
[fit] Group-like
[fit] Ring-like
[fit] Lattice-like
[fit] Module-like
[fit] Algebra-like
[fit] structures

[fit] Group-like
[fit] one binary operation

[fit] Ring-like
[fit] two binary operations,
[fit] often called addition and multiplication,
[fit] with multiplication distributing over addition.

[fit] Lattice-like
[fit] two or more binary operations,
[fit] including operations called meet and join,
[fit] connected by the absorption law

[fit] Module-like
[fit] composite systems involving two sets
[fit] and employing at least two binary operations

[fit] Algebra-like
[fit] composite system defined over two sets,
[fit] a ring R and an R-module M equipped with
[fit] an operation called multiplication

[fit] Group-like
[fit] structures


[fit] Magma

Magma
A type with a (closed) binary operation


$$A × A → A$$

protocol Magma {
  static func <> (lhs: Self, rhs: Self) -> Self
}


$$A × A → A$$

interface Magma<A> {
  readonly concat: (x: A, y: A) => A
}

[fit] Semigroup

[fit] Semigroup
A magma where the operation is associative


$$A × A → A$$

protocol Semigroup: Magma {}


$$A × A → A$$

interface Semigroup<A> extends Magma<A> {}

[fit] Semigroup Law
[fit] Associativity

[fit] Associativity
$$a <> (b <> c) ≅ (a <> b) <> c$$
$$a + (b + c) ≅ (a + b) + c$$
$$a × (b × c) ≅ (a × b) × c$$
$$a → (b → c) ≅ (a → b) → c$$

[fit] Monoid

[fit] Monoid
A semigroup with an identity element


$$A × A + 1 → A$$

protocol Monoid: Semigroup {
  static var empty: Self { get }
}


$$A × A + 1 → A$$

interface Monoid<A> extends Semigroup<A> {
  readonly empty: A
}

[fit] Monoid Law
[fit] Identity

[fit] Identity
$$a <> empty = empty <> a = a$$
$$a + empty = empty + a = a$$
$$a × empty = empty × a = a$$

[fit] Monoid
[fit] Examples

Sum
struct Sum<A: Numeric>: Monoid {
 let sum: A

  init(_ sum: A) {
    self.sum = sum
  }
  
  static func <> (lhs: Sum, rhs: Sum) -> Sum {
    self.init(lhs.sum + rhs.sum)
  }
  
  static var empty: Sum {
    0
  }
}

Sum
const Sum: monoid<number> = {
  empty: 0,
  concat: (u: number, v: number) => u + v
}

Product
struct Product<A: Numeric>: Monoid {
 let product: A

  init(_ product: A) {
    self.product = product
  }
  
  static func <> (lhs: Product, rhs: Product) -> Product {
    self.init(lhs.product * rhs.product)
  }
  
  static var empty: Product {
    1
  }
}

Product
const Product: monoid<number> = {
  empty: 1,
  concat: (u: number, v: number) => u * v
}

Endo
struct Endo<A>: Monoid {
  let call: (A) -> A

  init(_ call: @escaping (A) -> A) {
    self.call = call
  }
  
  static func <> (lhs: Endo<A>, rhs: Endo<A>) -> Endo<A> {
    .init { rhs.call(lhs.call($0)) }
  }
  
  static var empty: Endo<A> {
    .init { $0 }
  }
}

Endo
const Endo = <A>(): Monoid<Endo<A>> => ({
  empty: (a) => a,
  concat: (lhs: Endo<A>, rhs: Endo<A>) => rhs(lhs())
})

All
struct All: Monoid {
  let bool: Bool

  init(_ bool: Bool) {
    self.bool = bool
  }

  static func <> (lhs: Bool, rhs: Bool) -> Bool {
    .init(lhs.bool && rhs.bool)
  }

  static var empty: Bool {
    .init(true)
  }
}

All
const All: monoid<boolean> = {
  empty: true,
  concat: (x, y) => x && y
}

Any
struct Any: Monoid {
  let bool: Bool

  init(_ bool: Bool) {
    self.bool = bool
  }

  static func <> (lhs: Bool, rhs: Bool) -> Bool {
    .init(lhs.bool || rhs.bool)
  }

  static var empty: Bool {
    .init(false)
  }
}

Any
const Any: monoid<boolean> = {
  empty: false,
  concat: (x, y) => x || y
}

Array
extension Array: Monoid {
  static func <> (lhs: Array, rhs: Array) -> Array {
    lhs + rhs
  }

  static var empty: Array {
    []
  }
}

List
const List: monoid<Array<A>> = {
  empty: [],
  concat: (x, y) => x.concat(y)
}

String
extension String: Monoid {
  static func <> (lhs: String, rhs: String) -> String {
    lhs + rhs
  }

  static var empty: String {
    ""
  }
}

String
const String: monoid<string> = {
  empty: '',
  concat: (x, y) => x + y
}

Maybe
extension Optional: Monoid where Wrapped: Monoid {
  static func <> (lhs: Optioanl, rhs: Optional) -> Optional {
    switch (lhs, rhs) {
    case (.none, _):
      return rhs
    case (_, .none):
      return lhs
    case let (.some(l), some(r)):
      return .some(l <> r)
    }
  }

  static var empty: Optional {
    .none
  }
}

Maybe
export interface None {
  readonly _tag: 'None'
}

export interface Some<A> {
  readonly _tag: 'Some'
  readonly value: A
}

export type Option<A> = None | Some<A>

export const isSome: <A>(fa: Option<A>) => fa is Some<A> = _.isSome
export const isNone = (fa: Option<unknown>): fa is None => fa._tag === 'None'

export const Maybe = <A>(S: Semigroup<A>): Monoid<Option<A>> => ({
  empty: none,
  concat: (x, y) => (isNone(x) ? y : isNone(y) ? x : some(S.concat(x.value, y.value)))
})

use cases

performance optimization

reversing a list

O(N²)
reverse :: [a] -> [a]
reverse [] = []
reverse (a : as) = reverse as ++ [a]

List monoid
instance Monoid [a] where
  mempty = []
  mappend as bs = as ++ bs

[fit] Cayley theorem

[fit] Cayley theorem
Every monoid can be represented by a set of endo-functions.

type DList a = [a] -> [a]
rep :: [a] -> DList a
rep as = \xs -> as ++ xs
unRep :: DList a -> [a]
unRep f = f []
rep [] = id
rep (xs ++ ys) = rep xs . rep ys
rev :: [a] -> DList a
rev [] = rep []
rev (a : as) = rev as . rep [a]

O(N)
fastReverse :: [a] -> [a]
fastReverse = unRep . rev

Foldable
protocol Foldable {
  associatedtype A
  associatedtype B

  func foldr(_ folder : (A) -> (B) -> B, _ initial : B) -> B

  func foldl(_ folder : (B) -> (A) -> B, _ initial : B) -> B

  func foldMap<M : Monoid>(_ map : (A) -> M) -> M
}
https://github.com/alskipp/Monoid/commit/86b6f0f85e85f0eec5a005f092501f8dc8f2da80

Recursion schemes


[fit] How abstract algebra
[fit] solves data engineering (Podcast)

How the abstract algebra and probabilistic data structures help solve fast versus big data issues that many are struggling with.


## algebraic-types.md

      
                Raw

        
              algebraic-types.md
            
          
    autoscale: true
[fit] Algebraic
[fit] Types

Algebra


Symbols
Operations
Laws


0, 1, 2, x, y, z
+, –, ×, %
0 + x = x


Algebra


Symbols
Operations
Laws


Types
Type constructors
?


(Void, Int, Bool)
(Optional, Either)
?


Algebra


Symbols
Operations
Laws


Things
Ways to make
new things
Rules the
things follow


[fit] Zero


$$0$$

enum Never {}


$$0$$

type Void = never

[fit] One


$$1$$

struct Unit {}


$$1$$

type Unit = void

[fit] Two


$$2$$

enum Bool {
  case true
  case false
}


$$2$$

type Bool = False | True

[fit] Three


$$3$$

enum Three {
  case one
  case two
  case three
}


$$3$$

type Three = One | Two | Three

[fit] Addition


[fit] $$L + R$$


$$+$$

enum Either<L, R> {
  case left(L)
  case right(R)
}


$$+$$

type Either<L, R> = Left<L> | Right<R>

[fit] How many values of type
[fit] Either<Bool, Three>
[fit] are there?


$$+$$

Either<Bool, Three>
.left(.false)
.left(.true)
.right(.one)
.right(.two)
.right(.three)


$$+$$

Either<Bool, Three>
Left<False>
Left<True>
Right<One>
Right<Two>
Right<Three>


[fit] $$+$$ Laws


$$0 + X = X$$

Either<Never,X> ≅ X


$$X + Y = Y + X$$

Either<X,Y> ≅ Either<Y,X>

[fit] Multiplication


$$×$$

struct Pair<First, Second> {
  let first: First
  let second: Second
}


$$×$$

type Pair<First, Second> = [First, Second]

[fit] How many values of type
[fit] Pair<Bool, Three>
[fit] are there?


$$×$$

Pair<Bool, Three>
Pair(.false, .one)
Pair(.false, .two)
Pair(.false, .three)
Pair(.true, .one)
Pair(.true, .two)
Pair(.true, .three)


$$×$$

Pair<False,One>
Pair<False,Two>
Pair<False,Three>
Pair<True,One>
Pair<True,Two>
Pair<True,Three>


[fit] $$×$$ Laws


$$0 × X = 0$$


$$Pair&lt;Never,X&gt; ≅ Never$$


$$1 × X = X$$


$$Pair&lt;Unit,X&gt; ≅ X$$


$$X × Y = Y × X$$


$$Pair&lt;X,Y&gt; ≅ Pair&lt;Y,X&gt;$$


[fit] Exponentiation

A^R
struct Reader<R, A> {
  let run: (R) -> A
}

A^R
interface Reader<R, A> {
  (r: R): A
}

[fit] How many values of type
[fit] Bool^Three
[fit] are there?

A^R
Set<(Three) -> Bool>
(.false, .false, .false),
(.false, .false, .true),  
(.false, .true,  .true),  
(.false, .true,  .false), 
(.true,  .true,  .true), 
(.true,  .true,  .false), 
(.true,  .false, .false), 
(.true,  .false, .true),

[fit] A^R Laws

1^A = 1

$$A → Unit ≅ Unit$$


A¹ = 1

$$Unit → A ≅ A$$


$$(B × C)ᴬ = Bᴬ × Cᴬ$$


$$A → Pair&lt;B,C&gt; ≅ Pair&lt;A → B, A → C&gt;$$


$$Cᴮᴬ = (Cᴮ)ᴬ$$


$$Pair&lt;A,B&gt; → C ≅ A → B → C$$


[fit] Types
[fit] Algebraically

[fit] Partiality


$$1 + A$$


$$1 + A$$

struct Optional<A> {
  case none
  case some(A)
}


$$1 + A$$

type Option<A> = None | Some<A>

[fit] Recursive
[fit] Types

[fit] Lists


$$1 + A × List$$


$$1 + A × List$$

enum List<A> {
  case empty
  indirect case cons(A, List<A>)
}


$$1 + A × List$$

type List<A> = Nil | Cons<Pair<A, List<A>>>


$$List = 1 + A × List$$


$$List = 1 + A × List$$


$$List = 1 + A × (1 + A × List)$$


$$List = 1 + A × List$$


$$List = 1 + A × (1 + A × List)$$


$$List = 1 + A + (A×A) × List$$


$$List = 1 + A × List$$


$$List = 1 + A × (1 + A × List)$$


$$List = 1 + A + (A×A) × List$$


$$List = 1 + A + (A×A) × (1 + A × List)$$


$$List = 1 + A × List$$


$$List = 1 + A × (1 + A × List)$$


$$List = 1 + A + (A×A) × List$$


$$List = 1 + A + (A×A) × (1 + A × List)$$


$$List = 1 + A + (A×A) + (A×A×A) × List$$


$$List = 1 + A × List$$


$$List = 1 + A × (1 + A × List)$$


$$List = 1 + A + (A×A) × List$$


$$List = 1 + A + (A×A) × (1 + A × List)$$


$$List = 1 + A + (A×A) + (A×A×A)× List$$


$$List = 1 + A + (A×A) + (A×A×A) × (1 + A × List)$$


$$List = 1 + A × List$$


$$List = 1 + A × (1 + A × List)$$


$$List = 1 + A + (A×A) × List$$


$$List = 1 + A + (A×A) × (1 + A × List)$$


$$List = 1 + A + (A×A) + (A×A×A)× List$$


$$List = 1 + A + (A×A) + (A×A×A) × (1 + A × List)$$


$$List = 1 + A + (A×A) + (A×A×A) + (A×A×A×A) × List$$


$$...$$


$$List = 1 + A × List$$


$$List = 1 + A × List$$


$$List - A × List = 1$$


$$List = 1 + A × LiSt$$


$$List - A × List = 1$$


$$List × (1 - A) = 1$$


$$List = 1 + A × LiSt$$


$$List - A × List = 1$$


$$List × (1 - A) = 1$$


$$List = 1 / (1 - A)$$


$$List = 1 / (1 - A)$$

List<A> = 1 / (1 - A)
        = 1 + A + A×A + A×A×A + A×A×A×A + ...
        = 1 + A + A² + A³ + A⁴ + ...


[fit] Trees


$$T = 1 + A × T²$$


$$T = 1 + A × T²$$

enum Tree<A> {
  case empty
  indirect case node(A, Pair<Tree<A>, Tree<A>>)
}


$$T = 1 + A × T²$$

type Tree<A> = Empty | Node<A, Pair<Tree<A>, Tree<A>>>


$$T = 1 + A × T²$$


$$A × T² - T + 1 = 0$$


[fit] Quadratic equation
T<A> = (1 - √1-4A) % 2A


$$T = 1 + A × T²$$


$$A × T² - T + 1 = 0$$


$$1 + A + 2A² + 5A³ + 14A⁴ + ...$$


[fit] Algebraic
[fit] Structures


## process.md

      
                Raw

        
              process.md
            
          
    autoscale: true
[fit] Speed

[fit] Iteration
[fit] Deliver working software in
[fit] small batches of user value

[fit] Quality

[fit] Code Review

[fit] Code Review¹
[fit] Pairing

[fit] Sustainable Pace

[fit] Sustainable Pace²
[fit] An unstressed, well rested, not overworked
[fit] team that is happy with its job
[fit] will produce orders of magnitude better quality

[fit] Improvement

[fit] Reflection

[fit] Reflection
[fit] The team will regularly reflect
[fit] on how to become more effective,
[fit] then tune and adjust behavior accordingly
Footnotes


[Intro to Empirical Software Engineering: What We Know We Don't Know]((https://youtu.be/WELBnE33dpY?t=1698) ↩


Intro to Empirical Software Engineering: What We Know We Don't Know ↩


## tdd.md

      
                Raw

        
              tdd.md
            
          
    autoscale: true
[fit] TDD


[fit] $$λ$$-calculus


$$λ$$-calculus


Syntax
Name
Description


x
Variable
A character or string representing a parameter or mathematical/logical value


(λx.M)
Abstraction
Function definition (M is a lambda term). The variable x becomes bound in the expression


(M N)
Application
Applying a function to an argument. M and N are lambda terms


[fit] Let's think of a unit test
[fit] like function application

[fit] we'll vary our inputs
[fit] while asserting on our outputs

[fit] Unit test
[fit] Input → Output

[fit] Local reasoning
the idea that the reader can make sense of the code directly in front of them, without going on a journey discovering how the code works.

[fit] Pure
[fit] Functions

[fit] Pure Functions
The function return values are identical for identical arguments
The function application has no side effects

[fit] Curry-Howard-Lambek
[fit] correspondence

[fit] Intuitionistic Logic
[fit] ≅
[fit] Typed Lambda Calculus
[fit] ≅
[fit] Cartesian Closed Categories

[fit] Logic
[fit] ≅
[fit] Types
[fit] ≅
[fit] Categories

[fit] Curry-Howard-Lambek


Logic
Types
Categories


propositions
types
objects


proofs
terms
arrows


proof of proposition A
inhabitation of type A
arrow f: t → A


implication
function type
exponential


conjunction
product type
product


disjunction
sum type
coproduct


falsity
void type (empty)
initial object


truth
unit type (singleton)
terminal object T


[fit] Propositions
[fit] as types

[fit] proofs
[fit] as programs

[fit] normalization of proofs
[fit] as evaluation of programs

[fit] Curry-Howard-Lambek


Logic
Types
Categories


propositions
types
objects


proofs
terms
arrows


proof of proposition A
inhabitation of type A
arrow f: t → A


implication
function type
exponential


conjunction
product type
product


disjunction
sum type
coproduct


falsity
void type (empty)
initial object


truth
unit type (singleton)
terminal object T


[fit] implication
[fit] a → b
[fit] if a then b

[fit] Tagged


type Dollars = number & { readonly __tag: unique symbol };

[fit] Scoping
[fit] The extent of the area or subject matter
[fit] that something deals with or to which it is relevant.

[fit] Total Functions

Just another name for a regular function to make it clear that it is defined for all elements of its input.

head :: [a] -> a

safehead :: [a] -> Maybe a

type NonEmptyArray<T> = [T, ...T[]];

[fit] Parse don't validate

[fit] Make impossible
[fit] states impossible

[fit] Functions with side effects

A function that has an observable effect besides returning a value.

interface Writer<W, A> {
  (): [A, W]
}

[fit] Architecture

[fit] UI is a function of state

UI = fn(state)

[fit] Model–view–viewmodel (MVVM)

[fit] Moore machine

a finite-state machine whose output values are determined only by its current state.

[fit] elm

[fit] Redux

[fit] Janus

[fit] The Composable
[fit] Architecture

[fit] Property tests

[fit] Galaxy brain


[fit] Dependent types


[fit] Systems as Wiring Diagram Algebras


[fit] Fabulous Fortunes, Fewer Failures, and Faster Fixes from Functional Fundamentals

  
## txxxs.md

      
                Raw

        
              txxxs.md
            
          
    [fit] Write tests

[fit] Thank you for
[fit] attending my Tim Talk

[fit] Write txxxs

[fit] Feed
[fit] back

[fit] Write fewer
[fit] Runtime tests
^ Possibly fewer tests
^ Will show techniques to reduce the scope of what needs to be runtime tested
^ In some cases for things are hard to or nearly impossible to test otherwise

[fit] Write more
[fit] Compile-time
[fit] types
^ Types can be a form of testing, proving that the code does what you think it does

[fit] Rule of least power
[fit]
[fit]
[fit]
[fit] Parse, don't validate
[fit]
[fit]
[fit]
[fit] Make impossible
[fit] states impossible

[fit] Curry-Howard
[fit] Correspondence
^ A direct relationship between computer programs and mathematical proofs
^ Pictures and bios of Curry and Howard
^ Give a little explaination of your passion for mathematical thinking

[fit] Intuitionistic Logic
[fit] ≅
[fit] Typed Lambda Calculus

[fit] Logic
[fit] ≅
[fit] Types

[fit] Curry-Howard


Logic
Types


propositions
types


proofs
terms


proof of proposition A
inhabitation of type A


implication
function type


conjunction
product type


disjunction
sum type


falsity
void type (empty)


truth
unit type (singleton)


[fit] Propositions
[fit] as types

[fit] proofs
[fit] as programs

[fit] normalization of proofs
[fit] as evaluation of programs

[fit] Curry-Howard


Logic
Types


propositions
types


proofs
terms


proof of proposition A
inhabitation of type A


implication
function type


conjunction
product type


disjunction
sum type


falsity
void type (empty)


truth
unit type (singleton)


^ It's enough to have an instance (inhabitant) of a type to prove it


[fit] Curry-Howard


Logic
Types


propositions
types


proofs
terms


proof of proposition A
inhabitation of type A


implication
function type


conjunction
product type


disjunction
sum type


falsity
void type (empty)


truth
unit type (singleton)


[fit] implication
[fit] a → b
[fit] if a then b

[fit] Rule of least power

[fit] Parse, don't validate

[fit] Make impossible states impossible

[fit] Rule of least power

[fit] Parse, don't validate

[fit] Parsing?

[fit] Turning nebulous data
[fit] into structured data

const head = (i: Array<a>): a = {...}

const head = (i: Array<a>): Maybe<a> = {...}

export interface None {
  readonly _tag: 'None'
}

export interface Some<A> {
  readonly _tag: 'Some'
  readonly value: A
}

export type Maybe<A> = None | Some<A>

[fit] Make impossible states impossible

[fit] Red, Green, Refactor

[fit] Red, Green, Refactor
| Red | Green | Refactor |
| Types | Implementation | Refactor |
[fit] Type Driven Development?

[fit] Pragmatism

[fit] Notes

Ideally all examples are real code examples from GitHub
Names are not type safety examples?

https://github.com/chaturangalagama/clinic-manager/blob/b650ebb50ac3f4e467c578f5ba28fb9cf545a3d7/src/app/objects/response/PatientRegistryListResponse.ts


Impossible states examples?
*
Symbols	Operations	Laws
Types	Type constructors	?
(Void, Int, Bool)	(Optional, Either)	?
Syntax	Name	Description
x	Variable	A character or string representing a parameter or mathematical/logical value
(λx.M)	Abstraction	Function definition (M is a lambda term). The variable x becomes bound in the expression
(M N)	Application	Applying a function to an argument. M and N are lambda terms
Logic	Types	Categories
propositions	types	objects
proofs	terms	arrows
proof of proposition A	inhabitation of type A	arrow f: t → A
implication	function type	exponential
conjunction	product type	product
disjunction	sum type	coproduct
falsity	void type (empty)	initial object
truth	unit type (singleton)	terminal object T