- 簡介
- 陣列 Array
- 連結串列 Linked List & 雙向連結串列 Double Linked List
- 堆疊 Stack
- 佇列 Queue
- 二元搜尋樹 Binary Search Tree
- 平衡二元搜尋樹 Balancing Binary Search Tree, AVL Tree
- 紅黑樹 Red-Black Tree
- 二元堆積 Binary Heap
- 關聯陣列/對映/字典 Associative Array/ Map/ Dictionary
- 三元搜尋樹 Ternary Search Tree
- 互斥集Disjoint Set
是電腦中儲存、組織資料的方式,可以讓我們有效地儲存資料,並讓所有運算能最有效率地完成
演算法的運行時間是根據資料結構決定的,所以使用適當的資料結構來降低演算法的時間複雜度,如:
- 最短路徑演算法若無適當的資料結構,運行時間是O(N^2),使用(heap/priority queue)可以大幅降低運行時間至O(N*logN)
簡單而言,ADT是針對資料結構的「規範」或「描述」,像是物件導向語言裡面的interface,但不會實作細節
舉例堆疊的ADT描述:
- push(): 插入元素 item 至堆疊頂端
- pop(): 移除並回傳堆疊頂端的元素
- peek(): 看堆疊頂端的資料而不取出
- size(): 看堆疊的長度
每個ADT在底層都有相對應的資料結構去實作ADT裡定義過的行為(method)
| ADT | Data Structures |
|---|---|
| Stack | array, linked list |
| Queue | array, linked list |
| Priority Queue | heap |
| Dictionary/Hashmap | array |
描述演算法的效率(複雜度),舉例來說,A宅想要分享他的D槽給B宅,有以下幾種做法:
- 從台北騎車到屏東B宅家
- 用網路傳輸,不考慮被FBI攔截的情況
| 1GB | 1TB | 500TB | |
|---|---|---|---|
| 騎車運送硬碟 | 600 min | 600 min | 600 min |
| 網路傳輸 | 3 min | 3072 min | 1536000 min |
從上表來看,騎車這個選項雖然聽起來很蠢,但不管硬碟有多大,都能確保10個小時內可以送達—— O(1);至於網路傳輸隨著檔案越大,所需的時間也越長 —— O(N);從這裡就可以看出常數時間(constant time)和線性時間(linear time)的差別對效率的影響有多大了
在表現複雜度函數的時候,有幾個通用的規則:
- 多個步驟用加法: O(a+b)
def func():
# step a
# step b- 省略常數:
O(3n)O(n)
def func(lst):
for i in lst: # O(n)
# do something ...
for i in lst: # O(n)
# do something ...
for i in lst: # O(n)
# do something ...- 不同的input用不同的變數表示:
O(N^2)O(a*b)
def func(la, lb):
for a in la:
for b in lb:
# do something ...- 省略影響不大的變數:
O(n+n^2)O(n^2)
O(n^2) <= O(n+n^2) <= O(n^2 + n^2)
# n^2是主導的變項,所以省略n
def func(la):
for a in la: # O(n)
# do something ...
for a in la: # O(n^2)
for b in la:
# do something物件或值的集合,每個物件或值可以被陣列的索引(index, key)識別
- 索引從0開始
- 因為有索引,我們可以對陣列做隨機存取(Random Access)
優點:
- 隨機存取不用搜尋就能訪問陣列當中所有值,執行速度快O(1)
- 不會因為鏈結斷裂而遺失資料
- 循序存取快
缺點:
- 重建或插入陣列須要逐一複製裏頭的值,時間複雜度是O(N)
- 編譯的時候必須事先知道陣列的大小,這讓陣列這個資料結構不夠動態(dynamic)
- 通常陣列只能存同一種型別
- 不支援連結串列的共享
| 行為 | big O | |
|---|---|---|
| search | 搜尋 | O(1) |
| insert | 插入第一項 | O(N) |
| append | 插入最後一項 | O(1) |
| remove | 移除第一項 | O(N) |
| removeLast | 移除最後一項 | O(1) |
random indexing: O(1)
arr = [1, 2, 3]
arr[0]linear search: O(n)
max = arr[0]
for i in arr:
if i > max:
max = i- 節點包含
data和referenced object - 連結的方式是節點(node)記住其他節點的參考(reference)
- 最後一個節點的參考是NULL
優點
- 各節點型態、記憶體大小不用相同
- 動態佔用的記憶體,不須事先宣告大小
- 插入、刪除快O(1)
缺點
- 不支援隨機存取,只能循序存取(sequencial access),時間複雜度為O(N)
- 須額外空間儲存其他節點的參考
- 可靠性較差,連結斷裂容易遺失資料
- 難以向前(backward)訪問,可以用雙向連結串列來處理,不過會多佔用記憶體空間
| 行為 | big O | |
|---|---|---|
| search | 搜尋 | O(N) |
| insert | 插入第一項 | O(1) |
| append | 插入最後一項 | O(N) |
| remove | 移除第一項 | O(1) |
| removeLast | 移除最後一項 | O(N) |
註:連結串列沒有index,處理插入或移除第N項會需要先循序找到插入/移除位置,因此會需要O(N)的時間
以下的代碼是我實作的範例,有錯誤煩請指正。
主要概念是實作__getitem__來循序存取(indexing),另外Double Linked List支援反向存取,故訪問lst[0]和lst[-1]皆可以達成O(1)的時間複雜度
執行結果請參考travishen/gist/linked-list.md
from collections import Iterable
class Node:
def __init__(self, data=None, next_node=None):
self.data = data
self.next_node = next_node
def __repr__(self):
return 'Node(data={!r}, next_node={!r})'.format(self.data, self.next_node)
class LinkedList(object):
def __init__(self, inital_nodes=None):
self.head = None
self.inital_nodes = inital_nodes
# garbage collect
for node in self:
del node
if isinstance(inital_nodes, Iterable):
for node in reversed(list(inital_nodes)):
self.insert(node) # insert to head
elif inital_nodes:
raise NotImplementedError('Inital with not iterable object')
def __repr__(self):
return 'LinkedList(inital_nodes={!r})'.format(self.inital_nodes)
def __len__(self):
count = 0
for node in self:
count += 1
return count
def __setitem__(self, index, data):
self.insert(data, index)
def __delitem__(self, index):
self.remove(index, by='index')
def __getitem__(self, index):
count = 0
current = self.head
index = self.positive_index(index)
while count < index and current is not None:
current = current.next_node
count += 1
if current:
return current
else:
raise IndexError
def positive_index(self, index): # inplement negative indexing
"""
Use nagative indexing will increase O(N) time complexity
We can improve it with double linded list
"""
if index < 0:
index = len(self) + index
return index
def insert(self, data, index=0):
index = self.positive_index(index)
if self.head is None: # initial
self.head = Node(data, None)
elif index == 0: # insert to head
new_node = Node(data, self.head)
self.head = new_node
else: # insert to lst[index]
last_node = self[index]
last_node.next_node = Node(data, last_node.next_node)
return None # this instance has changed and didn't create instance
def search(self, data):
for node in self:
if node.data == data:
return node
return None
def remove(self, data_or_index, by='data'):
for i, node in enumerate(self):
if (by == 'data' and node.data == data_or_index) or (by == 'index' and i == data_or_index):
if i == 0:
self.head = node.next_node
node.next_node = None
else:
prev_node.next_node = node.next_node
break
prev_node = node
return None # this instance has changed and didn't create instance
class DoubleLinkedNode(Node):
def __init__(self, data=None, last_node=None, next_node=None):
self.data = data
self.next_node = next_node
self.last_node = last_node
if next_node:
next_node.last_node = self
class DoubleLinkedList(LinkedList):
def __init__(self, *args, **kwargs):
self.foot = None
super(DoubleLinkedList, self).__init__(*args, **kwargs)
def __repr__(self):
return 'DoubleLinkedList(inital_nodes={})'.format(self.inital_nodes)
def __getitem__(self, index):
"""
Support negative indexing in O(N) by setting footer
"""
count = 0
if index >= 0:
current = self.head
while count < index and current is not None:
current = current.next_node
count += 1
else:
current = self.foot
while count > (index + 1) and current is not None:
current = current.last_node
count -= 1
if current:
return current
else:
raise IndexError
def insert(self, data, index=0):
if self.head is None: # initial
self.head = self.foot = DoubleLinkedNode(data, None, None)
elif index == 0: # insert to head
new_node = DoubleLinkedNode(data, None, self.head)
self.head = new_node
else: # insert to lst[index]
last_node = self[index]
last_node.next_node = DoubleLinkedNode(data, last_node, last_node.next_node)
if last_node.next_node.next_node is None: # set foot
self.foot = last_node.next_node
return None # this instance has changed and didn't create instance - 低級別的內存管理(Low Level Memory Management),以C語言為例:
malloc()、free(): 見Heap Managementchart * chart_ptr = (chart*)malloc(30);: 取得30byte的heap memory
-
許多Windows的應用程式:工具列視窗切換、PhotoViewer
-
區塊鏈技術
- 推疊是一種抽象資料型態,特性是先進後出(LIFO, last in first out)
- 在高階程式語言,容易用array、linked list來實作
- 大部分的程式語言都是Stack-Oriented,因為仰賴堆疊來處理method call(呼叫堆疊, Call Stack)。可參考Call Stack, Scope & Lifetime of Variables,以及Python Function Calls and the Stack
| 行為 | big O | |
|---|---|---|
| push | 將資料放入堆疊的頂端 | O(1) |
| pop | 回傳堆疊頂端資料 | O(1) |
| peek | 看堆疊頂端的資料而不取出 | O(1) |
- call stack + stack memory
- 深度優先搜尋演算法(Depth-First-Search)
- 尤拉迴路(Eulerian Circuit)
- 瀏覽器回上一頁
- PhotoShop上一步(undo)
註:任何遞迴(recursion)形式的演算法,都可以用Stack改寫,例如DFS。不過就算我們使用遞迴寫法,程式最終被parsing還是Stack
def factorial(n, cache={}):
if n == 0: # declare base case to prevent stack overflow
return 1
return n * factorial(n-1)| stack memory | heap memory |
|---|---|
| 有限的記憶體配置空間 | 記憶體配置空間較大 |
| 存活時間規律可預測的 | 存活時間不規律不可預測的 |
| CPU自動管理空間(GC) | 使用者自主管理空間 |
| 區域變數宣告的空間不能更動 | 物件的值可以變動,如realloc() |
另外ptt有針對兩者佔用記憶體大小的討論stack v.s. heap sizes
class Stack(object):
def __init__(self, initial_data):
self.stack = []
self.initial_data = initial_data
if isinstance(initial_data, Iterable):
self.stack = list(initial_data)
else:
raise NotImplementedError('Inital with not iterable object')
def __repr__(self):
return 'Stack(initial_data={!r})'.format(self.initial_data)
def __len__(self):
return len(self.stack)
def __getitem__(self, i):
return self.stack[i]
@property
def is_empty(self):
return len(self.stack) == 0
def push(self, data):
self.stack.append(data)
def pop(self):
if not self.is_empty:
return self.stack.pop()
def peek(self):
return self.stack[-1]Using Lists as Stacks
>>> stack = [3, 4, 5]
>>> stack.append(6)
>>> stack.append(7)
>>> stack
[3, 4, 5, 6, 7]
>>> stack.pop()
7
>>> stack
[3, 4, 5, 6]
>>> stack.pop()
6
>>> stack.pop()
5
>>> stack
[3, 4]
- 佇列是一種抽象資料型態,特性是先進先出(FIFO, first in first out)
- 在高階程式語言,容易用array、linked list來實作
- 多個程序的資源共享,例如CPU排程
- 非同步任務佇列,例如I/O Buffer
- 廣度優先搜尋演算法(Depth-First-Search)
class Queue(object):
def __init__(self, initial_data):
self.queue = []
self.initial_data = initial_data
if isinstance(initial_data, Iterable):
self.queue = list(initial_data)
else:
raise NotImplementedError('Inital with not iterable object')
def __repr__(self):
return 'Queue(initial_data={!r})'.format(self.initial_data)
def __len__(self):
return len(self.queue)
def __getitem__(self, i):
return self.queue[i]
@property
def is_empty(self):
return len(self.queue) == 0
def enqueue(self, data):
return self.queue.append(data)
def dequeue(self):
return self.queue.pop(0)
def peek(self):
return self.queue[0]參考
- multiprocessing實作的的Queue
- Using Lists as Queues
>>> from collections import deque
>>> queue = deque(["Eric", "John", "Michael"])
>>> queue.append("Terry") # Terry arrives
>>> queue.append("Graham") # Graham arrives
>>> queue.popleft() # The first to arrive now leaves
'Eric'
>>> queue.popleft() # The second to arrive now leaves
'John'
>>> queue # Remaining queue in order of arrival
deque(['Michael', 'Terry', 'Graham'])主要的優點就是時間複雜度能優化至O(logN)
- 每個節點最多有兩個子節點
- 子節點有左右之分
- 左子樹的節點小於根節點、右子樹的節點大於根節點
- 節點值不重複
| Average case | Worst case | |
|---|---|---|
| insert | O(logN) | O(N) |
| delete | O(logN) | O(N) |
| search | O(logN) | O(N) |
以Python實作insert, remove, search,執行結果請參考gist
class Node(object):
def __init__(self, data):
self._left, self._right = None, None
self.data = int(data)
def __repr__(self):
return 'Node({})'.format(self.data)
@property
def left(self):
return self._left
@left.setter
def left(self, node):
self._left = node
@property
def right(self):
return self._right
@right.setter
def right(self, node):
self._right = node
class BinarySearchTree(object):
def __init__(self, root=None):
self.root = root
self.search_mode = 'in_order'
# O(logN) time complexity if balanced, it could reduce to O(N)
def insert(self, data, **kwargs):
"""Insert from root"""
BinarySearchTree.insert_node(self.root, data, **kwargs)
# O(logN) time complexity if balanced, it could reduce to O(N)
def remove(self, data):
"""Insert from root"""
BinarySearchTree.remove_node(self.root, data)
@staticmethod
def insert_node(node, data, **kwargs):
node_consturctor = kwargs.get('node_constructor', None) or Node
if node:
if data < node.data:
if node.left is None:
node.left = node_consturctor(data)
else:
BinarySearchTree.insert_node(node.left, data, **kwargs)
elif data > node.data:
if node.right is None:
node.right = node_consturctor(data)
else:
BinarySearchTree.insert_node(node.right, data, **kwargs)
else:
node.data = data
return node
@staticmethod
def remove_node(node, data):
if not node:
return None
if data < node.data:
node.left = BinarySearchTree.remove_node(node.left, data)
elif data > node.data:
node.right = BinarySearchTree.remove_node(node.right, data)
else:
if not (node.left and node.right): # leaf
del node
return None
if not node.left:
tmp = node.right
del node
return tmp
if not node.right:
tmp = node.left
del node
return tmp
predeccessor = BinarySearchTree.get_max_node(node.left)
node.data = predeccessor.data
node.left = BinarySearchTree.remove_node(node.left, predeccessor.data)
return node
def get_min(self):
return self.get_min_node(self.root)
@staticmethod
def get_min_node(node):
if node.left:
return BinarySearchTree.get_max_node(node.left)
return node
def get_max(self):
return self.get_max_node(self.root)
@staticmethod
def get_max_node(node):
if node.right:
return BinarySearchTree.get_max_node(node.right)
return node
def search_decorator(func):
def interface(*args, **kwargs):
res = func(*args, **kwargs)
if isinstance(res, Node):
return res
elif 'data' in kwargs:
for node in res:
if node.data == kwargs['data']:
return node
return res
return interface
@staticmethod
@search_decorator
def in_order(root, **kwargs):
"""left -> root -> right"""
f = BinarySearchTree.in_order
res = []
if root:
left = f(root.left, **kwargs)
if isinstance(left, Node):
return left
right = f(root.right, **kwargs)
if isinstance(right, Node):
return right
res = left + [root] + right
return res
@staticmethod
@search_decorator
def pre_order(root, **kwargs):
"""root -> left -> right"""
f = BinarySearchTree.pre_order
res = []
if root:
left = f(root.left, **kwargs)
if isinstance(left, Node):
return left
right = f(root.right, **kwargs)
if isinstance(right, Node):
return right
res = [root] + left + right
return res
@staticmethod
@search_decorator
def post_order(root, **kwargs):
"""root -> right -> root"""
f = BinarySearchTree.post_order
res = []
if root:
left = f(root.left, **kwargs)
if isinstance(left, Node):
return left
right = f(root.right, **kwargs)
if isinstance(right, Node):
return right
res = left + right + [root]
return res
def traversal(self,
order:"in_order|post_order|post_order"=None,
data=None):
order = order or self.search_mode
if order == 'in_order':
return BinarySearchTree.in_order(self.root, data=data)
elif order == 'pre_order':
return BinarySearchTree.pre_order(self.root, data=data)
elif order == 'post_order':
return BinarySearchTree.post_order(self.root, data=data)
else:
raise NotImplementedError()
def search(self, data, *args, **kwargs):
return self.traversal(*args, data=data, **kwargs)- OS file system
- 機器學習:決策樹
- 能保證O(logN)的時間複雜度
- 每次insert, delete都要檢查平衡,非平衡需要額外做rotation
- 判斷是否平衡:
| Average case | Worst case | |
|---|---|---|
| insert | O(logN) | O(logN) |
| delete | O(logN) | O(logN) |
| search | O(logN) | O(logN) |
不適合用在排序,時間複雜度為O(N*logN)
- 插入n個:O(N*logN)
- in-order迭代:O(N)
繼承上面BST繼續往下實作,有bug請協助指正,執行結果請參考gist
- 任一節點設定完left或right,更新該節點height
- 每個insert的call stack檢查檢查節點是否平衡,不平衡則rotate
class HNode(Node):
def __init__(self, *args, **kwargs):
super(HNode, self).__init__(*args, **kwargs)
self._height = 0
def __repr__(self):
return 'HNode({})'.format(self.data)
@property
def height(self):
return self._height
def set_height(self):
if self.left is None and self.right is None:
self._height = 0
else:
self._height = max(self.left_height, self.right_height) + 1
return self._height
@Node.left.setter
def left(self, node):
self._left = node
self.set_height()
@Node.right.setter
def right(self, node):
self._right = node
self.set_height()
@property
def sub_diff(self):
return self.left_height - self.right_height
@property
def left_height(self):
if self.left:
return self.left.height
return -1
@property
def right_height(self):
if self.right:
return self.right.height
return -1
@property
def is_balance(self):
return abs(self.sub_diff) <= 1
def balance(self, data):
if self.sub_diff > 1:
if data < self.left.data: # left left heavy
return self.rotate('right')
if data > self.left.data: # left right heavy
self.left = self.left.rotate('left')
return self.rotate('right')
if self.sub_diff < -1:
if data > self.right.data:
return self.rotate('left') # right right heavy
if data < self.right.data: # right left heavy
self.right = self.right.rotate('right')
return self.rotate('left')
return self
def rotate(self, to:"left|right"):
if to == 'right':
tmp = self.left
tmp_right = tmp.right
# update
tmp.right = self
self.left = tmp_right
print('Node {} right rotate to {}!'.format(self, tmp))
return tmp # return new root
if to == 'left':
tmp = self.right
tmp_left = tmp.left
# update
tmp.left = self
self.right = tmp_left
print('Node {} left rotate to {}!'.format(self, tmp))
return tmp # return new root
raise NotImplementedError()
class AVLTree(BinarySearchTree):
def __init__(self, *args, **kwargs):
super(AVLTree, self).__init__(*args, **kwargs)
def insert(self, data):
AVLTree.insert_node(self.root, data, tree=self) # pass self as keyword argument to update self.root
self.update_height()
def remove(self, data):
AVLTree.remove_node(self.root, data, tree=self) # pass self as keyword argument to update self.root
self.update_height()
def rotate_decorator(func):
def interface(*args, **kwargs):
node = func(*args, **kwargs)
data = args[1]
tree = kwargs.get('tree')
new_root = node.balance(data)
if node == tree.root:
tree.root = new_root
return interface
def update_height(self):
for n in self.traversal(order='in_order'):
n.set_height()
@property
def is_balance(self):
return self.root.is_balance
@rotate_decorator
def insert_node(*args, **kwargs):
return BinarySearchTree.insert_node(*args, node_constructor=HNode, **kwargs)
@rotate_decorator
def remove_node(*args, **kwargs):
return BinarySearchTree.remove_node(*args, **kwargs) - 相較於AVL樹,紅黑樹犧牲了部分平衡性換取插入/刪除操作時更少的翻轉操作,整體效能較佳(插入、刪除快)
- 不像AVL樹的節點屬性用height來判斷是否須翻轉,而是用紅色/黑色來判斷
- 根節點、末端節點(NULL)是黑色
- 紅色節點的父節點和子節點是黑色
- 每條路徑上黑色節點的數量相同
- 每個新節點預設是紅色,若違反以上規則:
- 翻轉,或
- 更新節點顏色
| Average case | Worst case | |
|---|---|---|
| insert | O(logN) | O(logN) |
| delete | O(logN) | O(logN) |
| search | O(logN) | O(logN) |
github上用python實作的範例:Red-Black-Tree
- 相較於Stack或Queue,對資料項目的取出順序是以權重(priority)來決定
- 常用heap來實作
- 是一種二元樹資料結構,通常透過一維陣列(one dimension array)
- 根據排序行為分成
min及max:- max heap: 父節點的值(value)或權重(key)大於子節點
- min heap: 父節點的值(value)或權重(key)小於子節點
- 必須是完全(compelete)二元樹或近似完全二元樹
註:
- heap資料結構跟heap memory沒有關聯
- 優勢在於取得最大權重或最小權重項目(root),時間複雜度為O(1)
| time complexity | |
|---|---|
| insert | O(N) + O(logN) reconsturct times |
| delete | O(N) + O(logN) reconsturct times |
- 堆積排序法(Heap Sort)
- 普林演算法(Prim's Algorithm)
- 戴克斯特拉演算法(Dijkstra's Algorithm)
- 是一種比較排序法(Comparision Sort)
- 主要優勢在於能確保O(NlogN)的時間複雜度
- 屬於原地演算法(in-place algorithm),缺點是每次排序都須重建heap——增加O(N)時間複雜度
- 在一維陣列起始位置為0的indexing:
操作可參考這篇文章:Comparison Sort: Heap Sort(堆積排序法)
用Python實作Max Binary Heap,請參考gist
class Heap(object):
"""Max Binary Heap"""
def __init__(self, capacity=10):
self._default = object()
self.capacity = capacity
self.heap = [self._default] * self.capacity
def __len__(self):
return len(self.heap) - self.heap.count(self._default)
def __getitem__(self, i):
return self.heap[i]
def insert(self, item):
"""O(1) + O(logN) time complexity"""
if self.capacity == len(self): # full
return
self.heap[len(self)] = item
self.fix_up(self.heap.index(item)) # check item's validation
def fix_up(self, index):
"""
O(logN) time complexity
Violate:
1. child value > parent value
"""
parent_index = (index-1)//2
if index > 0 and self.heap[index] > self.heap[parent_index]:
# swap
self.swap(index, parent_index)
self.fix_up(parent_index) # recursive
def fix_down(self, index):
"""
O(logN) time complexity
Violate:
1. child value > parent value
"""
parent = self.heap[index]
left_child_index = 2 * index + 1
right_child_index = 2 * index + 2
largest_index = index
if left_child_index < len(self) and self.heap[left_child_index] > parent:
largest_index = left_child_index
if right_child_index < len(self) and self.heap[right_child_index] > self.heap[largest_index]:
largest_index = right_child_index
if index != largest_index:
self.swap(index, largest_index)
self.fix_down(largest_index) # recursive
def heap_sort(self):
"""
O(NlogN) time complixity
"""
for i in range(0, len(self)):
self.poll()
def swap(self, i1, i2):
self.heap[i1], self.heap[i2] = self.heap[i2], self.heap[i1]
def poll(self):
max_ = self.max_
self.swap(0, len(self) - 1) # swap first and last
self.heap[len(self) - 1] = self._default
self.fix_down(0)
return max_
@property
def max_(self):
return self.heap[0]- 鍵、值的配對(key-value)
- 相較於樹狀資料結構,劣勢在於排序困難
- 主要操作:
- 新增、刪除、修改值
- 搜尋已知的鍵
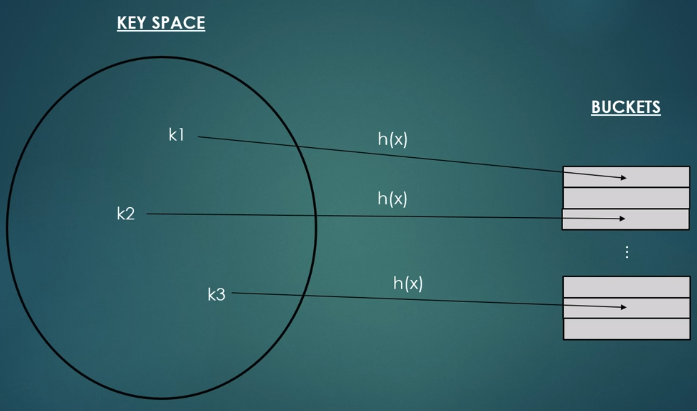
- division method: modulo operator
h(x) = n % m
n: number of keys, m: number of buckets
當多個key存取同一個bucket(slot),解決collision會導致時間複雜度提高
h(26) = 26 mod 6 = 2
h(50) = 50 mod 6 = 2
解法:
- chaining: 在同一個slot用linked list存放多個關聯
- open addressing: 分配另一個空的slot
- linear probing: 線性探測
- quadratic probing: 二次方探測,如1, 2, 4, 8...
- rehashing
Second Round皆有詳盡解說:
load factor(佔用率): n / m
- load factor會影響到存取的效能,因此須要根據使用率動態變更陣列大小;
- 舉例來說,Java觸發resize的時機點大約是佔用超過75%時、Python則約是66%
- 資料庫
- Network Routing
- Rabin-Karp演算法
- Hashing廣泛用於資料加密
參考:
- http://www.globalsoftwaresupport.com/use-prime-numbers-hash-functions/
- http://alrightchiu.github.io/SecondRound/hash-tableintrojian-jie.html#collision
以Python實作,請參考gist
from collections import Iterable
from functools import reduce
class HashTable(object):
def __init__(self, size=10):
self.size = 10
self.keys = [None] * self.size
self.values = [None] * self.size
def __repr__(self):
return 'HashTable(size={})'.format(self.size)
def put(self, key, value):
index = self.hash(key)
while self.keys[index] is not None: # collision
if self.keys[index] == key: # update
self.values[index] = value
return
index = (index + 1) % self.size # rehash
self.keys[index] = key
self.values[index] = value
def get(self, key):
if key in self.keys:
return self.values[self.hash(key)]
return None
def hash(self, key):
if isinstance(key, Iterable):
sum = reduce(lambda prev, n: prev + ord(n), key, 0)
else:
sum = key
return sum % self.size| Average case | Worst case | |
|---|---|---|
| insert | O(1) | O(N) |
| delete | O(1) | O(N) |
| search | O(1) | O(N) |
- 相較其他樹狀資料結構而言,佔用記憶體空間較小
- 只儲存string,不存NULL或其他物件
- 父節點可以有3個子節點:
left(less)、middle(equal)、right(greater) - 可以同時用來當作hashmap使用,也可以做排序
- 效能上比hashmap更佳,在解析key時是漸進式的(如
cat若root沒有c就不用繼續找了)
- autocompelete
- 拼字檢查
- 最近鄰居搜尋(Near-neighbor)
- WWW package routing
- 最長前綴匹配(perfix matching)
- Google Search
以Python實作,請參考gist
class Node(object):
def __init__(self, char):
self.char = char
self.left = self.middle = self.right = None
self.value = None
class TernarySearchTree(object):
def __init__(self):
self.root = None
def __repr__(self):
return 'TernarySearchTree()'
def put(self, key, value):
self.root = self.recursive(key, value)(self.root, 0)
def get(self, key):
node = self.recursive(key)(self.root, 0)
if node:
return node.value
return -1
def recursive(self, key, value=None):
def putter(node, index):
char = key[index]
if node is None:
node = Node(char)
if char < node.char:
node.left = putter(node.left, index)
elif char > node.char:
node.right = putter(node.right, index)
elif index < len(key) - 1:
node.middle = putter(node.middle, index+1)
else:
node.value = value
return node
def getter(node, index):
char = key[index]
if node is None:
return None
if char < node.char:
return getter(node.left, index)
elif char > node.char:
return getter(node.right, index)
elif index < len(key) - 1:
return getter(node.middle, index+1)
else:
return node
if value:
return putter
else:
return getter- 一堆沒有交集的集合,如10個學生分成4組
- 主要操作:
union、find、makeSet - 通常以linked list或tree來實作
- 訪問disjoint set中的任何節點都回傳同一個root value
set在union過程中會遇到不平衡的問題,有兩種最佳化方法:
- union by rank: 讓小的樹接到較大的樹
- path compression: 訪問節點時調整樹的結構,直接與root連結
- Kruskal: 檢查圖中是否有cycle
以Python實作,輸出請參考gist
class Edge:
"""Sortable edge in the graph"""
def __init__(self, weight, start, target):
self.weight = weight
self.start = start # Node
self.target = target # Node
def __repr__(self):
return 'Edge(weight={}, start={}, target={})'.format(self.weight,
self.start,
self.target)
def __cmp__(self, other):
return self.cmp(self.weight, other.weight)
def __lt__(self, other):
return self.weight < other.weight
class Node:
"""Node live in a graph / disjoint set"""
def __init__(self, name):
self.name = name
self.parent = None
self.set_ = None
def __repr__(self):
return self.name
parent = None
if self.parent:
parent = self.parent.name
return 'Node(name={}, parent={})'.format(self.name, parent)
class DisjointSet:
"""Represent a disjoint set"""
def __init__(self, node):
"""make set"""
self.nodes = set([node])
self.root = node
self.root.set_ = self
def __str__(self):
if not self.nodes:
return 'Empty'
return str(self.nodes)
def __len__(self):
return len(self.nodes)
@staticmethod
def find(node):
"""Find root node in nodes and do path compression"""
root = node
while root.parent is not None:
root = root.parent
# path compression
while node is not root:
temp = node.parent
node.parent = root
node = temp
return root
@staticmethod
def merge(s1, s2):
"""Merge two set base on """
if s1 is s2: # is equal
return
if len(s1) < len(s2): # s1 --> s2
s1.root.parent = s2.root
for n in s1.nodes: # point all node to new set
n.set_ = s2
s2.nodes.update(s1.nodes)
s1.nodes = set()
else: # s2 --> s1
s2.root.parent = s1.root
for n in s2.nodes: # point all node to new set
n.set_ = s1
s1.nodes.update(s2.nodes)
s2.nodes = set()