Keywords, topics: approximation, relative error, inverse, Chebyshev polynomial, Krylov, python
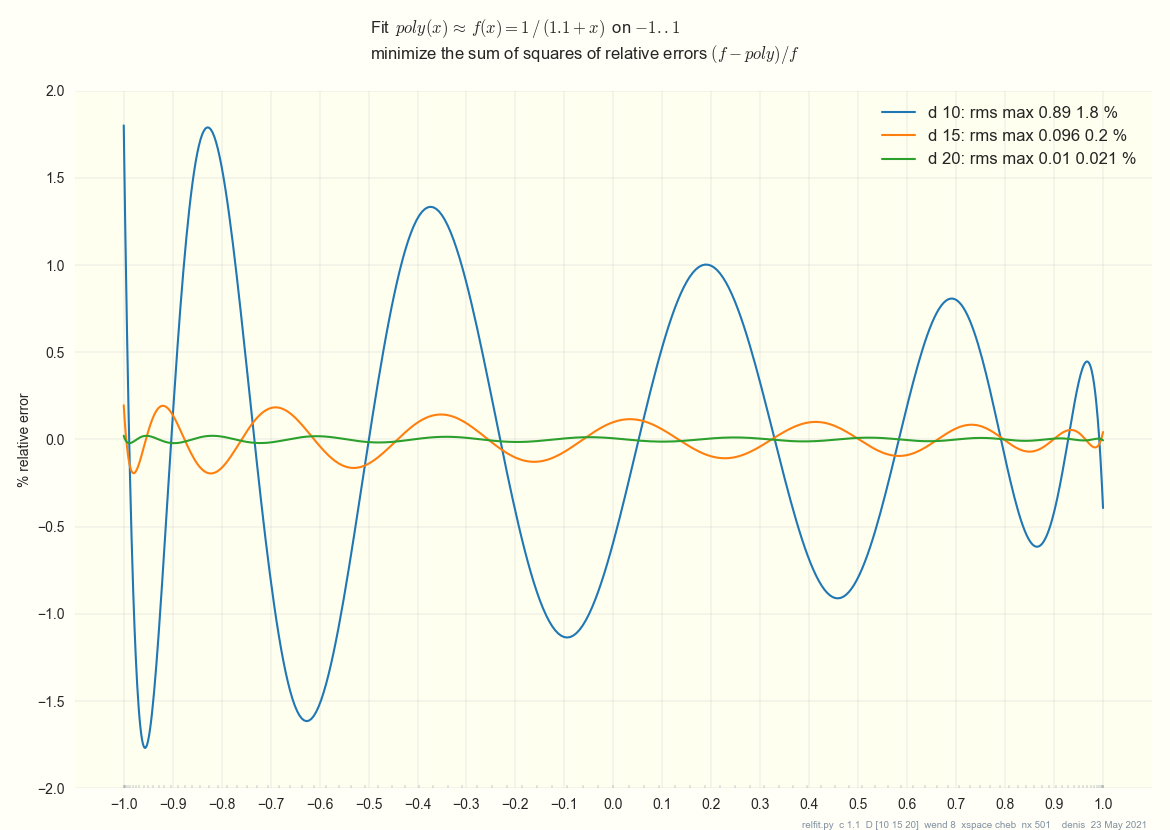
This plot shows polynomials of degrees 10, 15, 20
that fit 1 / x on the range 0.1 .. 2.1,
shifted to fits of 1 / (1.1 + x) on -1 .. 1.
Why relative (percent) error ?
Consider 1/x for x in the range 0.1 .. 2.1, 1/x steep to pretty flat:
plot 10 % relative error vs. 0.5 absolute error.
Say you want to solve a big linear system Ax = b, x = Ainverse b aka b \\ A.
poly(A) b might be a cheap approximation to b \\ A:
poly(A) * A ~ I
poly(A) ~ I \\ A
poly(A) b ~ b \\ A.
This is the Krylov subspace method in a nutshell. See e.g. Bindel, Cornell, Krylov subspaces (2019, 4 pages). His last sentence:
the right way to evaluate the convergence of Krylov methods in practice is usually to try them out, plot the convergence curves, and see what happens.
Don't expect any poly(x) ~ 1 / x to be very accurate near 0.
Matching poly( 0.1 ) ~ 10 is reasonable,
but poly( 0.001 ) ~ 1000 is unreasonable,
let alone matching the slope - 1 / x^2 near 0.
The error in approximating a matrix Ainverse depends strongly on 1 / (spectrum of A).
Iterative methods generally start with an A inside the circle |A - I| < 1.
If |A - I| < say 0.9, then poly10 above might give you a usable x0 = b \\ poly10(A).
|A - I| < 0.8 is better --
avoid edges, avoid big errors.
The code for fitting weighted least squares is little more than
def wfit( X, y, w=None, verbose=1 ):
""" weighted least squares fit: min w * (y - X @ coef)
-> Bag( coef sing fit diff relerr ... )
"""
...
np.linalg.lstsq( Xw, yw, rcond=1e-6 )
RMS(x), root-mean-square error, is the 2norm(x) that least-squares is minimizing, scaled by sqrt(n) so that RMS( all ones ) = 1 for any n. This is a better measure of goodness of fit than plain 2norm: more intuitive, and independent of n.
Weighted least squares ? To improve the approximation to 1 / x near x = 0 (or wherever you want), one can play with weights ... (There's an old paper with the title "Splendors and miseries of iteratively reweighted least squares".)
There are lots of ways of approximating Ainverse for big sparse A, and even more ways of combining different ones. Preconditioning "is an art, a science and an industry."
Moore's laws of speed, memory, price make old academic papers obsolete at about the same rate.
Chebyshev polynomials in numpy
class Cheblinop: a LinearOperator( A, poly ). \
cheers
-- denis 23 May 2021