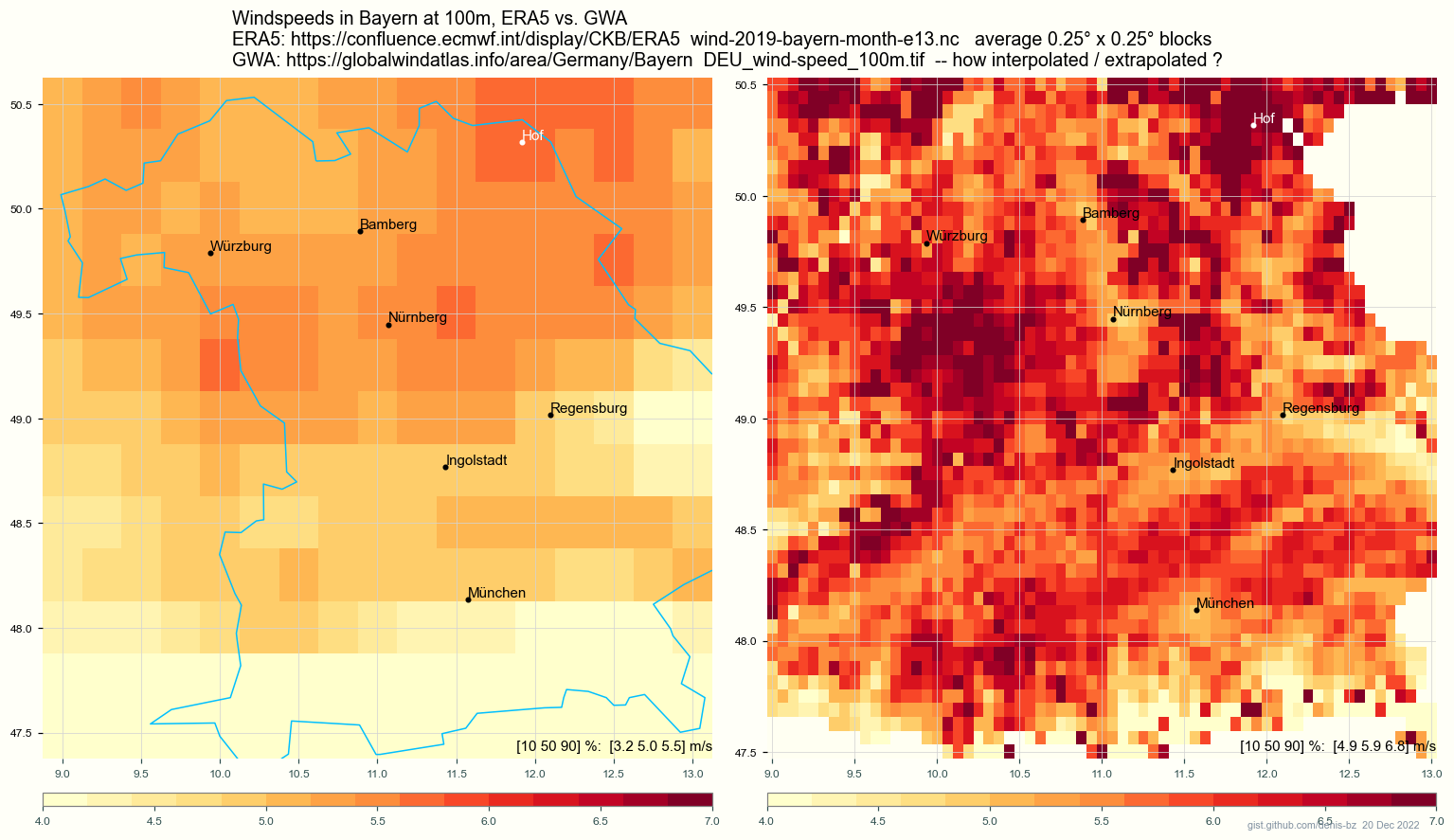
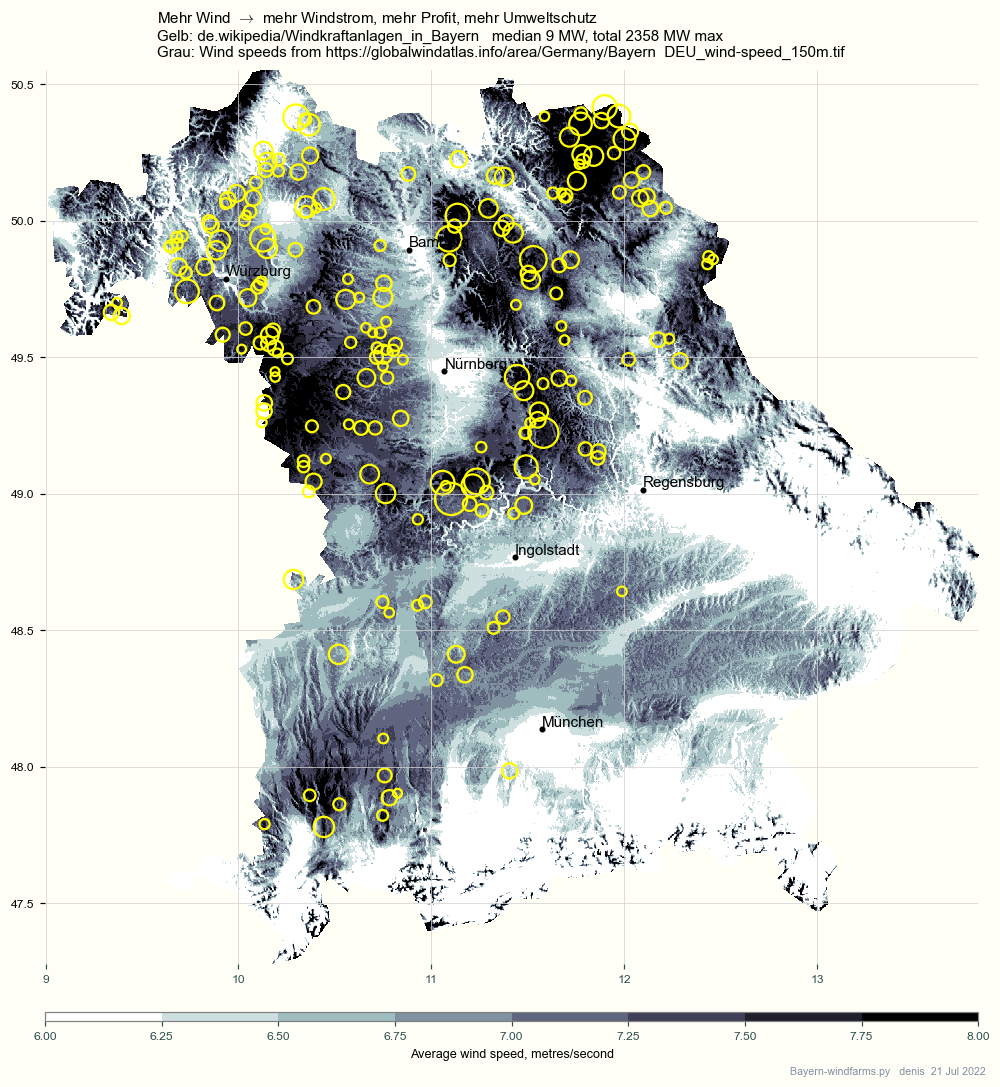
Keywords: Cosmo_rea6 DWD wind-data python numpy
Purpose:
DWD, the German Meteorological Service,
has wind data for Europe on a 6 x 6 km grid, from 1995 to August 2019, hourly,
at heights 10 100 .. 200m.
These are in 2 gigabyte files like
https://opendata.dwd.de/climate_environment/REA/COSMO_REA6/converted/hourly/2D/WS_100m.2D.201908.nc4
-- windspeed data at 100m for 2019 August.