Central differences like
diff1 = (f_{t+1} - f{t-1}) / 2, [0 -1 0 1 0] / 2
diff2 = (f_{t+2} - f{t-2}) / 4, [-1 0 0 0 1] / 4
approximate the derivative f'(t) much better then the
one-sided difference f_{t+1} - f_t;
see e.g. Wikipedia
Numerical differentiation.
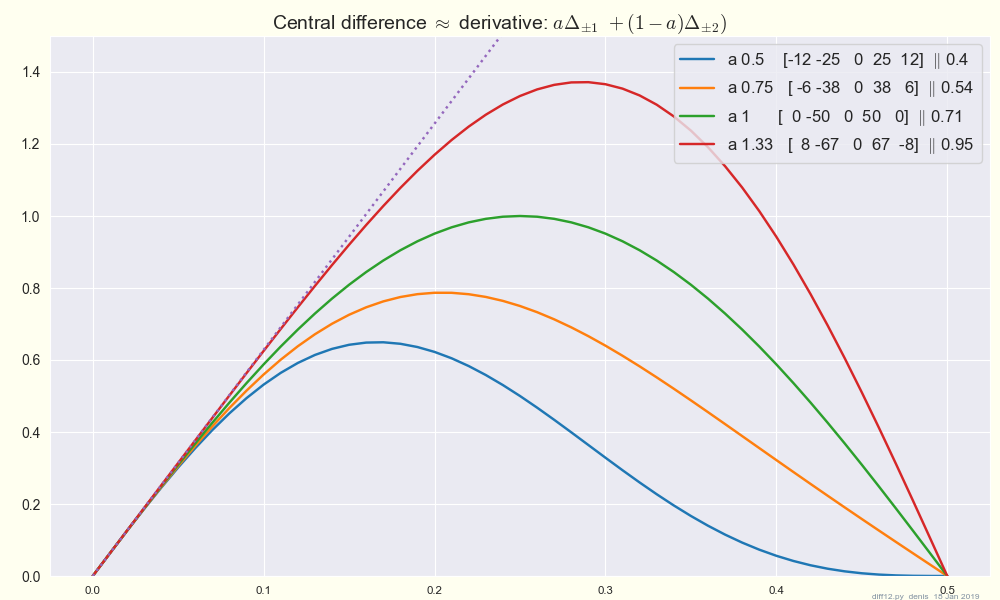
Is the average, (diff1 + diff2) / 2, much better than diff1 or diff2 alone ?
Are there better combinations a diff1 + (1 - a) diff2 ?
Let's plot the frequency response of a few:
This plot shows that 4/3 diff1 - 1/3 diff2, [1 -8 0 8 -1] / 12,
is surprisingly close to the ideal response
d/dt e^iwt = iw e^iwt (well, surprised me).
This is the top row in a table under Wikipedia
Finite difference coefficient .
FIR filters have an easy-to-calculate noise amplification factor, just the L2 norm (see Hamming, Digital Filters, p. 18 -- uncorrelated normally-distributed noise.) Amplifying noise by a factor > 1 is bad.
These are linear combinations of the one-sided differences
diff1 = (f_{t} - f{t-1}), [1 -1 0]
diff2 = (f_{t} - f{t-2}) / 2, [.5 0 -.5]
Here [1.5 -2 .5] from CRTaylor/calculator at -2 -1 0 looks terrible: try it on Nyquist-frequency input [1 -1 1 -1 ...] .
Floating-point roundoff noise can severely distort the finite-difference gradients / Jacobians used in optimizing noisy functions of many variables (scipy minimize*, Matlab fmincon), so slow down the whole optimization. The stepsizes in f( x +- step ) have of course a large effect on numerical gradients. The common default value sqrt( float64 eps ) ~ 1e-8 is theoretically good for smooth problems, but I think way too small for non-smooth. On one difficult optimization problem (MOPTA08, 124 variables, 68 nonlinear constraints, SLSQP), stepsize 5e-5 worked well -- 5000 times the default.
Adaptive stepsizes are common for ODEs, but rare ? for optimization.
cheers
-- denis 2019-01-19 jan
Theory and practice are closer in theory than they are in practice.