You should use this version instead; it's better.
Note that this uses a bilinear transform and so is not accurate at high frequencies.
Apply an A-weighting filter to a sound stored as a NumPy array.
Use Audiolab or other module to import .wav or .flac files, for example. http://www.ar.media.kyoto-u.ac.jp/members/david/softwares/audiolab/
Translated from MATLAB script (BSD license) at: http://www.mathworks.com/matlabcentral/fileexchange/69




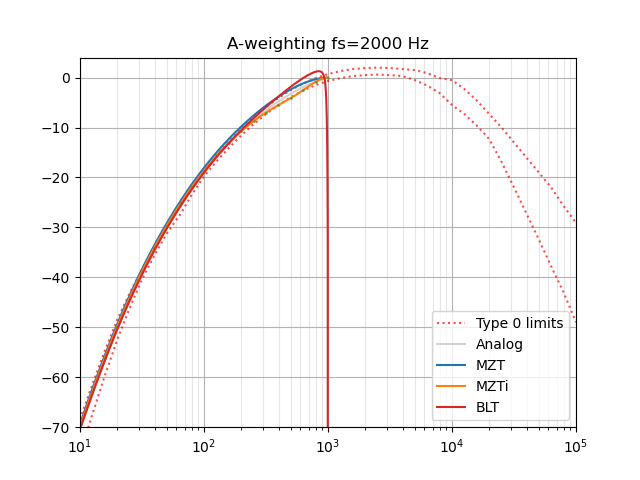


and maybe include bilinear as an option so people can compare with the results of other software?