A set is basically an array of unique items.
Ordered set.
[1, 2] != [2, 1]Unordered set.
{"a": 1, "b": 2} == {"b": 2, "a": 1}Symmetric difference. The set of elements in exactly one of A or B. The unique items when you combine A and B.
# {1,5,6,8} ∆ {2,5,8} = {1,2,6}
A = [1, 5, 6, 8]
B = [2, 5, 8]
# A ∆ B = [1, 2, 6]A is a superset of B. The A array has all items the B array has.
# true
A = [1, 2, 3, 4, 5, 6]
B = [1, 2, 3]
# true
A = [1, 2, 3]
B = [1, 2, 3]
# false
A = [1, 2, 4, 5, 6]
B = [1, 2, 3]
# false
A = [1, 2]
B = [1, 2, 3]A is a superset of B, but A != B. The A array has all items the B array has, but the two arrays aren't identical.
# true
A = [1, 2, 3, 4, 5, 6]
B = [1, 2, 3]
# false
A = [1, 2, 3]
B = [1, 2, 3]
# false
A = [1, 2, 4, 5, 6]
B = [1, 2, 3]
# false
A = [1, 2]
B = [1, 2, 3]Union. The set of elements which are in A, B, or both. The unique elements when A and B are concatenated.
# [1, 2, 3, 4, 5, 6]
A = [1, 2, 3, 4, 5, 6]
B = [1, 2, 3]
# [1, 2, 3]
A = [1, 2, 3]
B = [1, 2, 3]
# [1, 2, 3]
A = [1, 2]
B = [1, 2, 3]Intersection. The set of elements which are in both A and B. The duplicate elements when arrays A and B are concatenated.
# [1, 2, 3]
A = [1, 2, 3, 4, 5, 6]
B = [1, 2, 3]
# [1, 2, 3]
A = [1, 2, 3]
B = [1, 2, 3]
# [1, 2]
A = [1, 2]
B = [1, 2, 3]Empty set. Blank array.
[]a is an element of S. a is an item in the S array.
# true
a = 1
S = [1, 2, 3]
# false
a = 4
S = [1, 2, 3]Difference. Set theoretic complement. The items in the A array which are not in the B array.
# [2, 3]
A = [1, 2, 3]
B = [1]
# [2, 3]
A = [1, 2, 3]
B = [1, 4, 5, 6]The two-dimensional vector space of real numbers in mathematics.
Natural numbers. Integers that can physically exist, i.e. only positive integers. Has different meanings. Means either { 0, 1, 2, 3, …} or { 1, 2, 3, …}.
# true
1
# sometimes true
0
# false
-1Integers.
# true
1
# true
-1
# true
0Definition. Setting a variable. Saying "let's call the second thing the first thing".
# A := parseInt(1.0)
A = parseInt(1.0)Set. An array of items.
# {1, 2, 3}
[1, 2, 3]The set of all x for which P(x) is true.
squaredLessThan20 = (set) ->
result = []
for item in set
if item * item < 20
result.push(item)
result
# {n ∈ ℕ : n^2 < 20} = {1, 2, 3, 4}
squaredLessThan20([1, 2, 3, 4, 5, 6]) #=> [1, 2, 3, 4]Cardinality. The number of items in the set.
# |{3, 5, 7, 9}| = 4
[3, 5, 7, 9].lengthCross product. The cross product is a binary operation on two vectors in a three-dimensional Euclidean space that results in another vector which is perpendicular to the plane containing the two input vectors.
http://stackoverflow.com/questions/243945/calculating-a-2d-vectors-cross-product
# A = {1, 2}
# B = {x, y, z}
# A×B = {(a, b) : a A, b B}
# A×B = {(1, x), (1, y), (1, z), (2, x), (2, y), (2, z)}
# [[1, x], [1, y], [1, z], [2, x], [2, y], [2, z]]
A = [1, 2]
B = [x, y, z]
# crossProduct function??? Dot product.
# one dimensional vector
A = [1, 2, 3]
B = [4, 5, 6]
dotProduct = (a, b) =>
n = a.length # or b.length
i = 0
result = 0
while i < n
result += (a[i] * b[i])
i += 1
resultFunction f maps the set X into the set Y. Or, there is a function f such that X is converted to Y.
X = [1, 2, 3]
Y = [3, 2, 1]
f = array.reverse
f(X) == YFunction composition.
# f(x) := 2x
# g(x) := x + 3
# (f∘g)(x) = 2(x + 3)
f = (x) -> 2 * x
g = (x) -> x + 3
x = 10
f(g(x)) #=> 26The probability of the event A occurring given that B occurs.
A is an event whose probability is independent of event B.
The problem A can be polynomially reduced to the problem B.
W⊥ means the orthogonal complement of W (where W is a subspace of the inner product space V), the set of all vectors in V orthogonal to every vector in W.
Norm of the element x. The length of the array. Always positive.
[1, 2, 3].length #=> 3The inner product of u and v, where u and v are members of an inner product space.
# x = (2, 3)
# y = (−1, 5)
# ⟨x, y⟩ = 2 × −1 + 3 × 5 = 13
innerProduct = (u, v) ->
crossProduct(u) + crossProduct(v)
innerProduct([2, 3], [-1, 5]) #=> 13Determinant of a matrix.
exampleSum = (n) ->
sum = 0
i = 0
while i <= n
sum += ((n * (n + 1)) / 2)
i += 1
sum
exampleSum(10) #=> 605The sum A+B of two m-by-n matrices A and B is calculated with:
(A + B)i,j = Ai,j + Bi,j, where 1 ≤ i ≤ m and 1 ≤ j ≤ n.
addMatrices = (a, b) ->
result = []
for rowA, rowI in a
rowB = b[rowI]
rowResult = []
for columnA, columnI in rowA
columnB = rowB[columnI]
columnResult = columnA + columnB
rowResult.push(columnResult)
result.push(rowResult)
result
addMatrices([[1, 2], [3, 4]], [[5, 6], [7, 8]])
#=> [[1 + 5, 2 + 6], [3 + 7, 4 + 8]]
#=> [[6, 8], [10, 12]]The transpose of an m-by-n matrix A is the n-by-m matrix AT formed by turning rows into columns and vice versa:
(AT)i,j = Aj,i
transposeMatrix = (matrix) ->
result = []
columnCount = matrix[0].length
rowCount = matrix.length
# construct new arrays
i = 0
while i < columnCount
column = []
result[i] = column
i += 1
for row, i in matrix
for column, j in row
result[j][i] = column
result
transposeMatrix([[1, 2, 3], [4, 5, 6]])
#=> [[1, 4], [2, 5], [3, 6]]binomial = (n, k) ->
coeff = 1
i = n - k
coeff *= i while i++ < n
i = 1
coeff /= i while i++ < k
coeff
alert binomial(5, 2)It'd be cool if there was a library that could parse TeX-like jqmath format into code:
E("A ⊇ B", A: [1, 2, 3, 4, 5, 6], B: [1, 2, 3]) #=> trueunion = (a, b) ->
result = []
for aItem in a
for bItem in b
if aItem == bItem
result.push aItem
result
math = (string) ->
parts = string.split(" ∪ ")
union(eval(parts[0]), eval(parts[1]))
alert math("[1, 2, 3] ∪ [1, 2, 3, 4, 5]")#Average Degree of a Graph
What is this saying (from the Graph Theory book)??
Well, := means "I want to call the thing on the right the thing on the left". So call that ∑ equation d(g). It's arbitrary. He's saying d(v) is going to be called the "degree" of a vertex, which he's defining as "the number of edges on that vertex". Then he's saying d(G) is going to be called the "degree" of the whole graph. He's basically just naming his functions and variables!
Then 1/|V|. He defines V to be the number of vertices in a graph. So, number of items in an array, or array.length, so 1/vertices.length.
Then v∈V. That's saying "v in V", or "vertex in vertices", or "item in array". Add this to the ∑, and you have a for loop: "for each v in V", or "for each item in array".
So, for each item in the array, execute the function: d(v). Simple as that, that's a "summation".
All together. The degree of a graph is [arbitrarily] defined by this: for each vertex in the graph, count the number of edges, and divide by the number of vertices. That is, it's the average number of edges per vertex! Are you kidding me! All that just for a simple average?
Here's the equation again:
In code, that looks like this:
# d(v)
degree = (vertex) ->
vertex.edges.length
# d(G)
averageDegree = (graph) ->
sum = 0.0
for vertex in graph.vertices
sum += degree(vertex)
sum / graph.vertices.length
graph =
vertices: [
{edges: ["details", "we", "don't", "care", "about"]}
{edges: ["some", "more", "edges"]}
]
averageDegree(graph) #=> 4x = (set) ->
# magic!
set.length
subsetGreaterThanZero = (G) ->
x(G) > 0
P = subsetGreaterThanZero([-1, 0, 1, 2]) #=> [1, 2]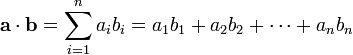


You might want to be careful drawing the comparison between a set and an array. A set contains distinct items, while an array has no such restriction.