Suppose $m \le n$, and $f(m) + g(m) > f(n) + g(n)$. Then $f(m) - f(n) + g(m) - g(n) > 0$. Consider $f(m) - f(n)$. We know
that $f(m) \le f(n)$. So $f(m) - f(n) \le 0$. Similarly for $g(m) - g(n)$. So their sum cannot be greater than 0.
This contradicts our earlier assertion, so $f(m) + g(m) \le f(n) + g(n)$, and $f(n) + g(n)$ is
monotonically increasing.
Suppose $m \le n$, and $f(g(m)) \gt f(g(n))$. Then $f(g(m)) - f(g(n)) \gt 0$. We know $g(m) \le g(n)$. Let
$o = g(m)$ and $p = g(n)$. We have $o \le p$. So $f(o) \le f(p)$. So $f(o) - f(p) \le 0$. This contradicts
our assumption that $f(g(m)) - f(g(n)) \gt 0$. So $f(g(m))$ is monotonically increasing.
Suppose $m \le n$, and $f(m) \cdot g(m) \gt f(n) \cdot g(n)$. Then $f(m) \cdot g(m) / (f(n) \cdot g(n)) \gt 1$.
We know $f(m) \le f(n)$, and that both are nonnegative, so we have $0 \le f(m)/g(n) \le 1$.
Similarly for $g(m)/g(n)$. So their product is less than or equal to 1. This contradictions our earlier assertion.
So $f(n) \cdot g(n)$ is monotonically increasing.
$$
\begin{align}
\lfloor 𝛼n \rfloor + \lceil (1-𝛼)n \rceil &= \lfloor 𝛼n \rfloor + \lceil n - 𝛼n \rceil \\
&= \lfloor 𝛼n \rfloor + n + \lceil -𝛼n \rceil \text{from 3.10} \\
&= \lfloor 𝛼n \rfloor + n - \lfloor 𝛼n \rfloor \text{from 3.3} \\
&= n \\
\end{align}
$$
We know $n^k$ is monotically increasing in $n$. Let $f(n)$ be the function that is $o(n)$.
We have $n \le n + f(n)$, so $n^k \le (n + f(n))^k$. Let $c_4$ be some constant greater than 1, and $c_1 = \frac{1}{c_4}$. We have $\frac{n^k}{c_4} \le n^k$. By transitivity, $\frac{n^k}{c_4} \le (n + f(n))^k$. So we have $0 \le c_1n^k \le (n + f(n))^k$ for all $n \ge 1$.
From the o-notation of $f(n)$, let $c_3$ and $n_2$ be constants such that $0 \le f(n) \lt c_3n$ for $n \ge n_2$. We have:
$$
\begin{align}
f(n) &\lt c_3n \\
n + f(n) &\lt n + c_3n \\
&\lt (1+c_3)n \\
\end{align}
$$
Since $n^k$ is monotonically increasing in $n$, we have:
$$
\begin{align}
(n+f(n))^k &\le ((1+c_3)n)^k \\
&\le (1+c_3)^k n^k
\end{align}
$$
So for $c_2 = (1 + c_3)^k$, $0 \le (n + f(n))^k \le c_2 n^k$ for all $n \ge n_2$. So for $n_1 = \text{max}(1,n_2)$, we have
$0 \le c_1n^k \le (n + f(n))^k \le c_2 n_k$ for all $n \ge n_1$. So $(n + o(n))^k = θ(n^k)$.
From inequality 3.2, we know $\lceil n \rceil \lt n + 1$, so it is asymtotically less than $n + o(n)$.
From this and the fact that $n^k$ is monotonically increasing in $n$, we have that
$0 \le {\lceil n \rceil}^k \le c_2n^k$ for $n \ge n_1$.
From the same inequality, we know $\lceil n \rceil \gt n - 1$, so it is greater than $n + (-1)$, and asymtotically
greater than $n + o(n)$. From this and the fact that $n^k$ is monotonically increasing,
$0 \le c_1 n^k \le {\lceil n \rceil}^k$ for all $n \ge n_1$. So ${\lceil n \rceil}^k = θ(n^k)$.
From the same inequality, we know $\lfloor n \rfloor \gt n - 1$, so (similar to the above reasoning),
it is asymtotically greater than $n+o(n)$. From this and the fact that $n^k$ is monotonically increasing in $n$, we have
that $0 \le n^k \le {\lfloor n \rfloor}^k$ for all $n \ge n_1$. From the same inequality, we know
$\lfloor n \rfloor \lt n + 1$, so it is asymtotically less than $n + o(n)$. From this and the fact that $n^k$
is monotonically increasing in $n$, we have that $0 \le {\lfloor n \rfloor}^k \le c_2 n^k$.
So ${\lfloor n \rfloor}^k = θ(n^k)$.
a.
$$
\begin{align}
a^{\log_b(c)} &= c^{\log_c(a^{\log_b(c)})} \\
&= c^{\log_b(c) \cdot \log_c(a)} \\
&= c^{\log_b(a)} \text{from 3.19}
\end{align}
$$
b. 3.26
We consider both $n!$ and $n^n$. Suppose we divide $n!$ by $(n)(n-1)(n-2)...(n-(n-2))$. That equals 1. Suppose we divide $n^n$ by $n^{n-1}$. That gives us $n$. Observe that $n^{n-1} \ge (n)(n-1)(n-2)...(n-(n-2))$. In both cases, there are $n-1$ terms in a product. But, except for the first term of $n$, all terms on the right-hand side are always a number less than $n$. This means we have divided $n!$ by a number less than what we've divided $n^n$ by, and yet it comes out to 1, compared to $n$ in the other case.
Consider any values of $c \ge 1$. We can choose $n_0 = 2$ and $0 \le n! \lt cn^n$ for all $n \ge n_0$. This can be seen by observing the behavior of $n!$ compared to $n$ after dividing each by the above respective numbers. $n!$ is reduced to $1$ while $n^n$ is reduced to $n$, which is greater than $1$ for all $n \ge n_0$.
Consider any value for $c \lt 1$. Let $c = 1/c_1$. $c_1$ is necessarily greater than 1. Choose $n_0 = {c_1}^2$. After dividing $n!$ and $n$ by the above respective values, we have 1 compared with $n$, where $n$ is at least ${c_1}^2$. Multiplying this minimum value of $n$ by $1/c_1$ gives $c_1$, which is greater than 1. Values of $n$ larger than ${c_1}^2$ will just outpace the value of 1 by a growing margin. So $0 \le n! \lt cn^n$ when $c = 1/c_1$ for all $c_1 > 1$ and $n \ge n_0$ where $n_0 = {c_1}^2$.
So for all $c > 0$, we can find $n_0$ such that $0 \le n! \lt cn^n$ for all $n \ge n_0$.
So $n! = o(n^n)$.
b. 3.27
Let's consider $2^n$ and $n!$. Assumes $n \ge 5$. Divide $2^n$ by $2^4 = 16$. This leaves $2^{n-4}$. Divide $n!$ by $4! = 24$. This leaves $(n)(n-1)(n-2) ... (5)$. There are $n-4$ terms remaining in both expressions. We have shrunk $n!$ more than we have shrunk $2^n$, since we divided it by a larger divisor. Now divide $2^{n-4}$ by $2^{(n-4)-1}$. Divide $(n)(n-1)(n-2)...(5)$ by all of its terms except for $n$. We are dividing both expressions by a number which is the product of $(n-4)-1$ terms. In the case of the $n!$ expression, all of the terms were larger than the number 2 (we already got rid of $(4)(3)(2)(1)$, so only terms of 5 and higher were remaining). In the case of the $2^n$ expression, all of the terms were 2. So again, we shrunk the $n!$ expression more than the $2^n$ expression by using a larger divisor on it. We are left with 2 for the $2^n$ expression and $n$ for the $n!$ expression. So despite shrinking the $n!$ expression by more than the $2^n$ expression, it still outpaces $2^n$.
That is, it is obvious that $2 \lt n$ for all $n \ge 3$.
Let $c \ge 1$. Let $n_0 = 3c$. Multiplying $2^n$ by $c$ will result in $2c$ after performing the above operations. If we shrink $n!$ using the above logic, and let $n_0 = 3c$, then $n!$ will become $3c$ when $n = n_0$. $2c \lt 3c$. For larger values of $n$, the disparity between $2^n$ and $n!$ will grow in favor or $n!$. So given any $c \ge 1$, we have $0 \le c2^n \lt n!$ for all $n \ge \text{max}(5,3c)$.
Let $c = 1/c_1$, where $c_1 > 1$. Multiplying $2^n$ by $c$ will yield $2/c_1$. We seek the inequality $2/c_1 \lt n$, or $2 \lt c_1 n$. This is true for all $n \ge 2$, since $c_1 \gt 1$. We choose $n_0 = 5$ since we assumed as much when doing our earlier operations. So when $c = 1/c_1$, $0 \le c 2^n \lt n!$ for all $n \ge n_0$.
So for all $c > 0$, we can find $n_0$ such that $0 \le c 2^n \lt n!$ for all $n \ge n_0$.
So $n! = ω(2^n)$.
b. 3.28
$$
\begin{align}
\lg(n!) &= \lg \left(\sqrt{2 \pi n} {\frac{n}{e}}^n (1 + θ(\frac{1}{n})) \right) \\
&= \lg \sqrt{2 \pi n} + \lg({\frac{n}{e}}^n) + \lg(1 + θ(\frac{1}{n})) \\
&= \frac{1}{2} \lg{2 \pi n} + n \lg n - n \lg e + \lg(1 + θ(\frac{1}{n})) \\
&= \frac{1}{2} \lg{2 \pi} + \frac{1}{2} \lg n + n \lg n - n \lg e + \lg(1 + θ(\frac{1}{n})) \\
\end{align}
$$
We drop insignificant terms.
$$
\begin{align}
\lg(n!) &= n \lg n + \lg(1 + θ(\frac{1}{n})) \\
\end{align}
$$
Let us consider $\lg(1 + θ(\frac{1}{n}))$. Let $f(n)$ be the unnamed function described by $θ(\frac{1}{n})$. For
some large enough $n_0$, we have $0 \le f(n) \le \frac{c_2}{n}$ for all $n \ge n_0$. Let us replace
$θ(\frac{1}{n})$ with $\frac{c_2}{n}$. We then have:
$$
\begin{align}
\lg(1 + θ(\frac{1}{n})) &= \lg(1 + \frac{c_2}{n}) \\
&= \lg \frac{n + c_2}{n}
\end{align}
$$
Which is insignificant compared to $n \lg n$. So even though we used an expression
that maximizes $f(n)$, it turned out not to influence the running time
of the larger expression. So $\lg(n!) = θ(n \lg n)$.
c. Let $f(n)$ be the unnamed function $θ(n)$ refers to. We have $0 \le c_1 n \le f(n) \le c_2 n$ for all $n \ge n_0$,
where $n_0$ is the sufficiently large, positive minimum $n$ required to make the inequality hold true.
Strictly increasing functions are monotonically increasing.
Since $\lg$ is strictly increasing for $n \gt 0$, for all $n \ge n_0$, we have $\lg(c_1 n) \le \lg(f(n)) \le \lg(c_2 n)$.
We add the constraint that $n_0$ be large enough so that $0 \le \lg(c_1 n)$. Then we have:
$$
\begin{align}
0 &\le \lg(c_1 n) \le \lg(f(n)) \le \lg(c_2 n) \\
\end{align}
$$
Consider the left side of the inequality, the lower bound. Let $c_1 = \frac{c_3}{c_4}$.
This gives us $\lg(\frac{c_3}{c_4} n)$. Consider $\frac{1}{2} \lg n$ as a replacement for $\lg(c_1 n)$.
This yields $\lg n^{\frac{1}{2}}$.
Make each be the exponent on 2. We have: $2^{\lg(\frac{c_3}{c_4} n)} = \frac{c_3 n}{c_4}$.
and $2^{\lg{n^\frac{1}{2}}} = n^{\frac{1}{2}}$. Divide each by $n^{\frac{1}{2}}$. We then have
$\frac{c_3 n}{c_4 n^{\frac{1}{2}}} = \frac{c_3 n^{\frac{1}{2}}}{c_4}$ and $\frac{n^\frac{1}{2}}{n^{\frac{1}{2}}} = 1$.
Take the difference of these two expressions:
$$
\begin{align}
\frac{c_3 n^{\frac{1}{2}}}{c_4} - 1 &= \frac{c_3 n^{\frac{1}{2}} - c_4}{c_4}
\end{align}
$$
This is greater than 0 when $c_3 n^{\frac{1}{2}} \gt c_4$, which is true when:
$$
\begin{align}
n^{\frac{1}{2}} &\gt \frac{c_4}{c_3} \\
n &\gt (\frac{c_4}{c_3})^2
\end{align}
$$
So for $n \ge (\frac{c_4}{c_3})^2 + 1$, $\frac{1}{2} \lg n$ is the smaller of the two expressions
we examined.
So we can use it to achieve $0 \le \frac{1}{2} \lg n \le lg(f(n))$ for all $n \ge (\frac{c_4}{c_3})^2 + 1$. We
can name $c_5 = \frac{1}{2}$ as the first lower-bound constant we will use to show $f(n) = θ(\lg n)$.
We now turn our attention to the right side of the inequality. Let $c_2 = \frac{c_6}{c_7}$. This gives us
$\lg \frac{c_6 n}{c_7}$.
Let us consider $5 \lg n$ as a replacement for this expression. This yields $\lg n^5$. Make
each the exponent on 2. This gives $2^{\lg \frac{c_6 n}{c_7}} = \frac{c_6 n}{c_7}$ and
$2^{\lg n^5} = n^5$. Divide each by $n$:
$$
\begin{align}
\frac{c_6}{c_7} \\
n^4 \\
\end{align}
$$
Take the difference:
$$
\begin{align}
n^4 - \frac{c_6}{c_7} = \frac{c_7 n^4 - c_6}{c_7}
\end{align}
$$
which is greater than 0 when:
$$
\begin{align}
c_7 n^4 &\gt c_6 \\
n^4 &\gt \frac{c_6}{c_7} \\
n &\gt \sqrt[4]{\frac{c_6}{c_7}}
\end{align}
$$
So for $n \ge \sqrt[4]{\frac{c_6}{c_7}} + 1$, $5 \lg n$ is the larger expression of the two we
examined. Let $c_8 = 5$. We have $0 \le \lg f(n) \le c_8 \lg n$ for all $n \ge \sqrt[4]{\frac{c_6}{c_7}} + 1$.
Let $n_1 = \text{max}((\frac{c_4}{c_3})^2 + 1, \sqrt[4]{\frac{c_6}{c_7}} + 1)$. Then:
$$
\begin{align}
0 \le c_5 \lg n \le \lg f(n) \le c_8 \lg n \\
\end{align}
$$
for all $n \ge n_1$. So $\lg(θ(n)) = θ(\lg n)$.
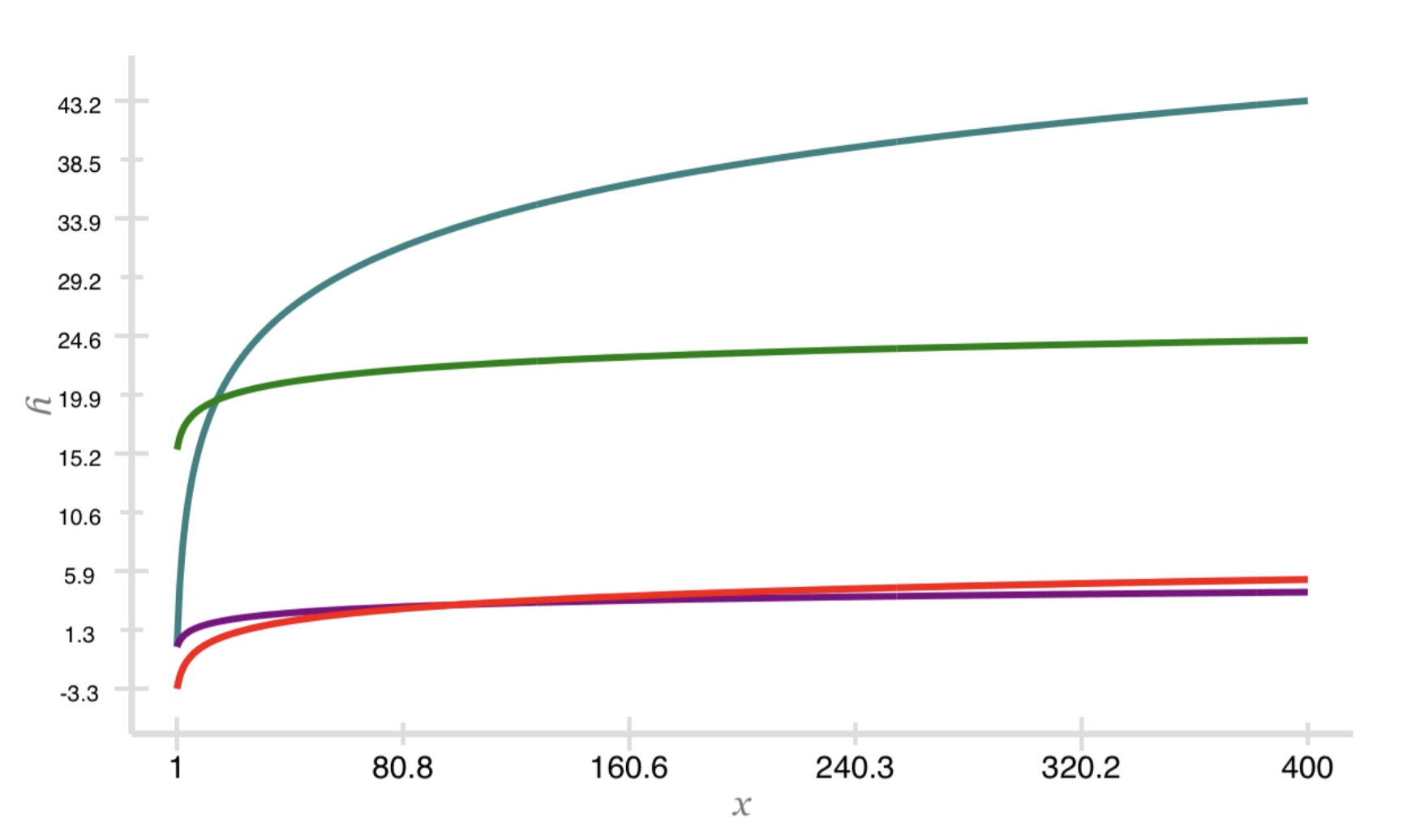
Here is a plot with $c_3 = 1$, $c_4 = 10$, $c_5 = \frac{1}{2}$, $c_6 = 50,000$, $c_7 = 1$, and $c_8 = 5$.
Here, $n_1 = \text{max}((\frac{c_4}{c_3})^2 + 1, \sqrt[4]{\frac{c_6}{c_7}} + 1) = \text{max}(100 + 1, 14.953 + 1) = 101$.
The aqua line is $5 \lg n$. The green line is $\lg \frac{c6}{c7} n$. The red line is $\lg \frac{c3}{c4} n$.
The purple line is $\frac{1}{2} \lg n$. The aqua and purple lines become the upper and lower bounds, respectively.