Skip to content

Instantly share code, notes, and snippets.

@mimoo

mimoo/ECC.md

Last active March 28, 2021 12:19
Show Gist options
  • Star 2 You must be signed in to star a gist
  • Fork 2 You must be signed in to fork a gist
  • Save mimoo/2f365c1f5a08a642f6d05fcbe9656055 to your computer and use it in GitHub Desktop.
Save mimoo/2f365c1f5a08a642f6d05fcbe9656055 to your computer and use it in GitHub Desktop.
Download ZIP
Elliptic Curve Cryptography
Raw
ECC.md

Elliptic Curve Cryptography (ECC)

Abstract

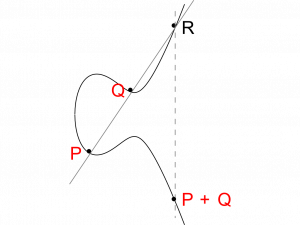
ECC is about a group created via:

  • a 2-dimension elliptic curve: an equation with unknowns x and y
    • every Elliptic Curve follows this formula: y2 + a1 x y + a3 y = x3 + a2 x2 + a4 x + a6 (for some specified a1, a2, a3, a4, a6)
    • actually, it can be shorten to this y2 = x3 + a x + b (short weierstrass form) in practice because the characteristic (order of a prime field) 2 and 3 points in prime fields (except for binary (GF(2x)) and GF(3x) curves)
    • a curve of characteristic 2 (defined over GF(2x)) can be simplified to y2 + xy = x3 + ax2 + b
    • a curve of characteristic 3 (defined over GF(3x)) can be simplified to y2 = x3 + x2 + b
  • a finite field GF(p^m). But in practice today we mostly use curves in GF(p) where the elliptic curve's points will have coordinates modulo p.
  • an addition operation (called group law): + will be defined (geometricaly) over these points.

Since coordinates are modulo a field, our crypto curve in reality looks more like this:

crypto curve

For example, NIST P-256 is defined on:

  • the curve of equation y^2 = x^3-3x+41058363725152142129326129780047268409114441015993725554835256314039467401291
  • coordinates of the points are taken modulo p = 2^256 - 2^224 + 2^192 + 2^96 - 1
  • the addition operation is the typical one.

To my knowledge the same addition operation is used in ECC (see the figure below). For it to work the group needs an identity point, which does not exist. So we add a fictive point called "the point at infinity" and often written a large O.

addition

To do crypto with all of that, you use the group as you use a group with normal (FF)DH or DSA.

A curve can always be expressed in Weierstrass normal form: y^2 = 4 x^3 - a x - c

There exist different types of curves:

  • Curves in short-Weierstrass form
  • Montgomery Curves
  • Twisted Edwards Curves
  • and probably some others?

The number of points in a subgroup is called the group order. Coincidentally, the number of times a point P has to be added to itself to result in the point at infinity is also called the order of P.

The torsion group of an ECC is the set of points that have a finite order (some points can add themselves ad infinitum).

Efficiency

There are different ways to see points, different representations allow for different levels of efficiency when it comes to computing point addition. For example you have affine coordinates (the normal (x,y)) and projective coordinates

You can also compress points: since you can easily recover the y-coordinate from the x-coordinate. One can just store the x-coordinate and the sign of y.

Security

ECC works in a group, not in a field, and is hence not prone to strong attacks on normal (FF)DH like the index calculus and the number field sieve (NFS) algorithms.

Yet, there are still attacks to be aware of:

  • twist-security.
    • "all curves are twist secure in the following sense. Either the number of rational points on the curve and its twist are both prime, or, if the curve is Montgomery compatible, both orders are four times a prime.".
    • djb page
  • invalid curve attacks. TKTK
  • anomalous curve. TKTK
  • binary curves. TKTK
  • small subgroup attacks: same as with normal (FF)DH. One can verify public keys received to make sure they are in the right subgroup. Interestingly, the main group of an ECC can have a prime order (unlike normal (FF)DH). If the order is not prime, we call the small factor the co-factor. (Curve25519 has a co-factor of 8.)
  • MOV attack: if there exists a pairing from a curve to a weak finite field, then we can attack the finite field itself (which is easier)
  • The Frey-Rück Attack: another pairing attack
  • typical DLOG attacks: Pohlig-Hellman, Pollard Rho, Baby-Step-Giant-Step. These attacks work in groups, so they are as efficient in (FF)DH as in ECDH. It's easy to counter them by using large parameters though.

Timeline

Curve Standards

  • ANSI X9.62 (1999)
  • IEEE P1363 (2000)
  • SEC 2 (2000): includes the bitcoin curve secp256k1.
  • NIST FIPS 186-2 (2000)
  • ANSI X9.63 (2001)
  • Brainpool (2005): the german curves from BSI
  • NSA Suite B (2005)
  • ANSSI FRP256V1 (2011): the french curves
  • curve25519/curve448 defined in RFC 7748 (2016)
  • Barreto-Lynn-Scott (BLS) curves: BLS12-381 is one of them. Curve for pairings.

Types of Curves

  • long weierstrass form (every elliptic curve is defined like that)
  • short weierstrass form (if char != 2 and 3)
  • montgomery (just a change of variable from the short weierstrass form)
  • extended jacobi quartic form
  • (twisted) hessian form
  • (twisted) Edward form
    • this is "birationnaly" equivalent to a short weierstrass form, meaning that there is a mapping between the two curves but it's not perfect and is missing some points.
  • (twisted) jacobi intersection form

or alternative representations:

  • Hessian curve
  • Edwards curve
  • Twisted curve
  • Twisted Hessian curve
  • Twisted Edwards curve
  • Doubling-oriented Doche–Icart–Kohel curve
  • Tripling-oriented Doche–Icart–Kohel curve
  • Jacobian curve
  • Montgomery curve

Elliptic Curve Generators (or curve on demand)

Algorithms

Points representation

Resources

Pages

  • safecurves: A comparison of all the standards from djb

Slides

Articles

Papers

Standards

Sign up for free to join this conversation on GitHub. Already have an account? Sign in to comment