This blog created for F# Advent 2016 (English)
Full source code can be found here
- 2016-12-10
- New performance test - Anthony Lloyd (@AnthonyLloyd) suggested that I compare against Prime.Vmap.
- New performance test - Added comparison to an immutable map based on
System.Collections.Generic.Dictionary - FSharp.Core 4.4.0 - Switched to FSharp.Core 4.4.0. This improved the performance of F# Map by an order of magnitude. F# Map still benefits from a custom comparer.
- Bug fixes - Fixed an issue in "my" maps that caused the Remove performance results to be better than expected.
- 2016-12-11
- New performance test - Henrik Feldt (@haf) suggested that I compare against Imms.ImmMap.
- New performance test - Added performance tests that varies the data size
- 2017-02-26
- Updated performance numbers - Bryan Edds (@bryanedds) has been tweaking on
Prime.Hmap - Moved images into repo - Instead of using imgur which is getting out of hand I put the images in the repo.
- 2017-03-14
- New performance test - Maksim Volkau (@dadhi) submitted a new test case for ImTools.
This blog started with me experimenting with the persistent hash map in clojure and comparing it to various implementations in .NET. I found the existing .NET implementations lagging in terms of performance and I was wondering why that is, especially since FSharpx.Collections' persistent hash map seems to be a port of the clojure persistent hash map.
A persistent hash map resembles the classic .NET type Dictionary<K, V> in that it's a hash table from K to V. However, while Dictionary<K, V> is mutable a persistent hash map is immutable.
When you set a new key value pair you get a reference to a new persistent hash map, leaving old one unmodified. This is exactly how F# Map works.
A persistent hash map is an immutable data structure that supports efficient lookup.
In F# immutable data structures are considered to be preferable over mutable data structures because in general it's easier to write correct programs with immutable data structures.
I think performance is an extremely important property for the long-term survivability of technology. If you have to functional equivalent libraries I think it's most likely that the performant library will survive.
A problem with immutable data structures is they seldomly perform as well as mutable data structures. As Chris Okasaki says in in the introduction to Purely Functional Data Structures: functional programming's stricture against destructive (i.e. assignments) is a staggering handicap, tantamount to confiscating a master chef's knives. Like knives, destructive updates can be dangerous when misused, but tremendously effective when used properly.
Chris Okasaki showed in his book that immutable data structures can be made to have decent complexity (Big O).
However, there is more to performance than just the complexity metric. It also comes down to very specific details on how the algorithm is implemented. For example, should you model the data structure using a ADT, abstract class or interface?
For immutable data structures to thrive I believe they also have to be performant.
The clojure and FSharpx.Collections persistent hash map is based around Phil Bagwell's ideal hash trie but adapted in various ways.
The ideal hash trie works by taking the hash of a key and using it to lookup a key value.
What follows is a brief illustration of how an ideal hash trie works but for details I recommend that you read Phil Bagwell's paper
Root Trie
0x0 - null , null
0x1 - null , null
0x2 - "A" , 1
0x3 - null, , Sub Trie
0x0 - "B" , 2
0x1 - "C" , 3
0x2 - ...
0x4 - ...
Let's say we want to find key "B". We hash the key, let's assume the hash is 0x03. We use the bits 0-3 (3) as position into the root trie:
Root Trie
0x0 - null , null
0x1 - null , null
0x2 - "A" , 1
0x3 - null, , Sub Trie <== HERE
0x0 - "B" , 2
0x1 - "C" , 3
0x2 - ...
0x4 - ...
The key is null at position 3 which means the value holds a sub trie. We use the bits 4-7 (0) as a position into the sub trie.
Root Trie
0x0 - null , null
0x1 - null , null
0x2 - "A" , 1
0x3 - null, , Sub Trie
0x0 - "B" , 2 <== HERE
0x1 - "C" , 3
0x2 - ...
0x4 - ...
The key is not null and thus we are at a key value, we compare the input key with the key in the trie and since they match we found the value 2.
If the hash was 0x00 we would immediately end up at a null , null key value pair meaning there's no match in the trie.
Phil Bagwell's ideal hash tries groups the hash into groups of 5 bits, here we used 4 bits for clarity.
The clojure persistent hash maps are based around ideal hash trie but makes some modifications. From PersistentHashMap.java
/*
A persistent rendition of Phil Bagwell's Hash Array Mapped Trie
Uses path copying for persistence
HashCollision leaves vs. extended hashing
Node polymorphism vs. conditionals
No sub-tree pools or root-resizing
Any errors are my own
*/Path copying was added to make the hash trie immutable. This means that whenever a new key value is inserted the nodes in the path from root to key value are copied.
Let's say we would like to replace the value of key "B" with 6 in the trie below:
Root Trie
0x0 - null , null
0x1 - null , null
0x2 - "A" , 1
0x3 - null, , Sub Trie
0x0 - "B" , 2
0x1 - "C" , 3
0x3 - ...
0x4 - null, , Sub Trie
0x0 - "E" , 4
0x1 - "F" , 5
0x3 - ...
The updated trie looks like this afterwards
Root Trie <== This is a new object
0x0 - null , null
0x1 - null , null
0x2 - "A" , 1
0x3 - null, , Sub Trie <== This is a new object
0x0 - "B" , 6 <== Updated to 6
0x1 - "C" , 3
0x3 - ...
0x4 - null, , Sub Trie <== This is shared with previous trie
0x0 - "E" , 4
0x1 - "F" , 5
0x3 - ...
Phil Bagwell's ideal hash trie uses extended hash whenever two keys have the same hash. This is not available in Java nor .NET and thus clojure has introduced a special node called HashCollisionNode for the case when all keys in a node have the same hash.
Phil Bagwell's ideal hash trie uses flags to discern between the different node types, in Java and .NET it often makes more sense to use polymorphism where the nodes share a common interface.
Some optimization techniques to minimize dynamic memory allocation that made little sense for Java.
As clojure is a dynamic language the IPersistentHashMap interface uses Object as key and value type. Therefore, the INode interface uses Object key and value type as well.
FSharpx.Collections.PersistentHashMap seems to have copied the design of the INode interface but added type-safety through generics to the interface. However, the use of Object as key and value means there will be boxing of value types like integers, creating additional heap pressure.
The INode in FSharpx.Collections interface is defined as this:
type internal INode =
abstract member assoc : int * int * obj * obj * Box -> INode
abstract member assoc : Thread ref * int * int * obj * obj * Box -> INode
abstract member find : int * int * obj -> obj
abstract member tryFind : int * int * obj -> obj option
abstract member without : int * int * obj -> INode
abstract member without : Thread ref * int * int * obj * Box -> INode
abstract member nodeSeq : unit -> (obj*obj) seqThere are 3 types that implement INode
ArrayNodeHashCollisionNodeBitmapIndexedNode
ArrayNode holds an array of INode with fixed size of 32. Elements in the array are allowed to be null. The hash is used to lookup the correct node, like this:
member this.tryFind(shift, hash, key) =
let idx = mask(hash, shift) // Select the correct 5 bits from the hash
let node = this.array.[idx] // Lookup the node
if node = Unchecked.defaultof<INode> then None else // Node is null, bail out
node.tryFind(shift + 5, hash, key) // Check child nodeHashCollisionNode is an array of key values where all keys have the same hash:
member this.find(shift, hash, key) =
let idx = this.findIndex(key) // Find index of key
if idx < 0 then null else // Not found, bail out
if key = this.array.[idx] then this.array.[idx+1] else null // If key is equal we found itMore interesting is, the BitmapIndexedNode. This a compressed version of ArrayNode. If an ArrayNode is sparsely populated it means most of the nodes in the array are null wasting a lot of space.
BitmapIndexedNode has a 32 bit bitmap that indicates what nodes would be set in ArrayNode but the array in a BitmapIndexedNode is compressed in that has no null nodes.
What is done during lookup is that one decides the index of the node we are interested in will have. Then we check the corresponding bit in the bitmap, if that is set we mask so we keep all of the bits lower and count them. This is our index into the compressed array.
Let's say bitmap is: 0x123 = 0b0001_0010_0011. We are interested in the node at position 8, that bit is set in the bitmap. We mask all bits lower than bit 8 ==> 0b0000_0010_0011. We count the number of bits in the masked bitmap ==> 4
The node we are interested in has location 4 in the compressed array.
In code it looks like this:
member this.find(shift, hash, key) =
let bit = bitpos(hash, shift) // Compute bit to check depending on hash
if this.bitmap &&& bit = 0 then null else // If bit is not set then bail
let idx' = index(this.bitmap,bit) * 2 // Compute index in compressed array
let keyOrNull = this.array.[idx']
let valOrNode = this.array.[idx'+1]
if keyOrNull = null then // keyOrNull is null, meaning valOrNode has to be an INode
(valOrNode :?> INode).find(shift + 5, hash, key)
else
if key = keyOrNull then // keyOrNull is not null meaning it's a key, check for equality
valOrNode // Ok, good
else
null // Nothing foundIn order for hash tries to be performant it's important that we have an efficient algorithm to count set bits in an integer. Luckily people have come up with crazy and wonderful algorithms for this purpose.
I was wondering why there was significant performance difference between clojure and FSharpx.Collections. I spent a lot of time reviewing the code and building identical test cases to see if I could find a performance bug. However, I reached a point where I made no progress. This was when I decided to implement a persistent hash map myself to get a better understanding.
I copied large parts of the design of persistent hash map in clojure and FSharpx.Collections but made some changes based purely on personal preferences.
- No
ArrayNode- Array nodes were used as an optimization for bitmap nodes but since they require an extra null check and takes more memory I decided against them seeing the parallel bit counting algorithm is rather performant. - Up to 16 sub nodes per node - The ideal hash tries, clojure and Fsharpx.Collections both uses up to 32 sub nodes in a sub node. 32 sub nodes per node means a max depth of 7. With 16 sub nodes per node the max depth is 8, not a huge difference but because of path-copying it also makes insertion/removal somewhat cheaper.
KeyValueNode- clojure and FSharpx.Collections usenullkey values as a flag to indicate if the value should be interpreted as a node or a value. For clojure this makes sense as all values areObjectthat hasnullas a valid value. In .NET we need to box keys and values to havenullas a valid value adding heap pressure. In addition, we need to cast the value into a node to call it, this adds a type-check per level. Therefore I addedKeyValueNodethat hold a non-boxed key and value.- Hash Code Caching - Each KeyValueNode caches the key hash code to avoid recomputation of hash codes as this can be expensive.
- Parallel bit counting - The best parallel bit counting algorithm I could find is used over lookup-tables.
- .NET idiomatic
TryFind-TryFinduses the .NET idiom of'K*[<Out>] rv : byref<'V> -> boolover F# idiom of'K -> 'V option. The reason is that'T optionwill create an object that needs collecting which will affect lookup performance. System.IEquatable<'K>used overequality- For performance. See appendix for an in-depth discussion.- Abstract class over interface - The interface of
PersistentHashMapwill be an abstract class. This seems to be a faster option for persistent hash tables over ADT or .NET Interfaces. - No
TransientNode- The usage of transient nodes in clojure and FSharpx.Collections is intended to speed-up performance during bulk inserts into an empty map. During my performance testing my impression was that the performance improvement was too small to motivate transient nodes. Anyway, it's possible to add transient nodes later if needed.
This is the interface of PersistentHashMap
type [<AbstractClass>] PersistentHashMap<'K, 'V when 'K :> System.IEquatable<'K>> =
class
static member internal Empty : PersistentHashMap<'K, 'V>
#if PHM_TEST_BUILD
member CheckInvariant : unit -> bool
#endif
member IsEmpty : bool
member Visit : v : ('K -> 'V -> bool) -> bool
member Set : k : 'K -> v : 'V -> PersistentHashMap<'K, 'V>
member TryFind : k : 'K*[<Out>] rv : byref<'V> -> bool
member Unset : k : 'K -> PersistentHashMap<'K, 'V>
#if PHM_TEST_BUILD
abstract internal DoCheckInvariant : uint32 -> int -> bool
#endif
// TODO: Why aren't these tagged as internal in the generated assembly
abstract internal DoIsEmpty : unit -> bool
abstract internal DoVisit : OptimizedClosures.FSharpFunc<'K, 'V, bool> -> bool
abstract internal DoSet : uint32 -> int -> KeyValueNode<'K, 'V> -> PersistentHashMap<'K, 'V>
abstract internal DoTryFind : uint32*int*'K*byref<'V> -> bool
abstract internal DoUnset : uint32 -> int -> 'K -> PersistentHashMap<'K, 'V>
endThe interface is intended to be minimal but complete. The PersistentHashMap module uses the interface to implement F# idiomatic functions like toArray.
CheckInvariant is used during property testing (FsCheck obviously) to check that the invariants still hold true.
The nodes implementing the base class:
EmptyNode- An empty nodeKeyValueNode- A singleton node, hold Key and Value (as well as Hash Code) without boxing themBitmapNodeN- The core nodeBitmapNode1- Special case of BitmapNodeN when N = 1BitmapNode16- Special case of BitmapNodeN when N = 16 meaning all bits are set in the bitmapHashCollisionNodeN- Handles hash collision
Even though there are differences compared to FSharpx.Collection the DoTryFind in BitmapNodeN looks very similar to to tryFind FSharpx.Collections.
override x.DoTryFind (h, s, k, rv)=
let bit = bit h s // Compute bit to test based on hash code and current shift
if (bit &&& bitmap) <> 0u then // Is the bit set?
let localIdx = localIdx bit bitmap // Ok, compute the localIdx (using popCount)
nodes.[localIdx].DoTryFind (h, (s + TrieShift), k, &rv)
else
falseI selected the following data structures to compare:
- Mutable Dictionary - Implemented a naive immutability map based on
System.Collections.Generic.Dictionary<_, _>. - Persistent Hash Map (C#) - "My" Map written in C#
- Persistent Hash Map (F#) - "My" Map written in F#
- Red Black Tree - A simplistic implementation of a Red Black Tree (similar to Map)
- FSharpx.Collections.PersistentHashMap
- Prime.Vmap - Anthony Lloyd (@AnthonyLloyd) suggested that I compare against Prime.Vmap
- Imms.ImmMap - Henrik Feldt (@haf) suggested that I compare against Imms.ImmMap
- System.Collections.Immutable.ImmutableDictionary
- FSharp.Collections.Map
- FSharp.Collections.Map' - This is a patched version of Map which allows a custom compare function
- clojure.PersistentHashMap - Running on JVM
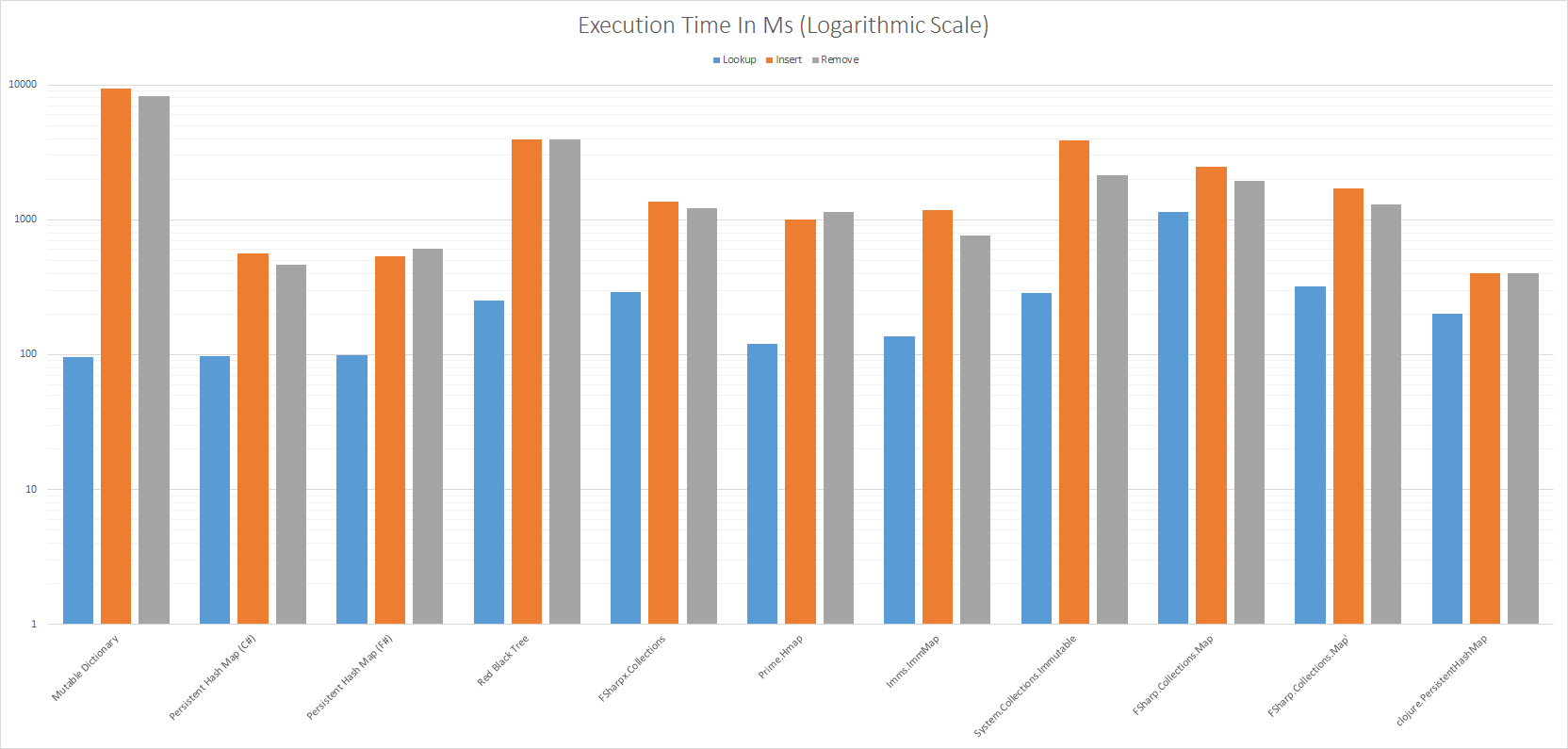
I run three test cases on the selected data structures:
- Lookup - Looking up all the values in a map created by Insert
- Insert - Creating a new map from 100 elements (data contains some duplicates)
- Remove - Removing all the values in a map created by Insert
I run each test case 40,000 times per data structure and collect the elapsed time as well a GC Collection Counts. All numbers are compared against the F# Persistent Hash Map
To be able to compare the Java code with .NET code I implemented a simple random generator to ensure the test data is identical.
I merely estimated the Red Black Tree removal time as I never implemented remove (too hard for me).
Note the scale on the y-axis is logarithmic to make the times comparable.
As expected the map based on System.Collections.Generic.Dictionary<_, _> has the best Lookup performance but also has the worst performance for Insert and Remove. This is because to support immutability a full copy is taken whenever a key is added or removed. If your code can accept destructive updates System.Collections.Generic.Dictionary<_, _> performs a lot better.
We see that F# Map Lookup performance is quite poor but with a custom comparer it does a lot better. It turns out that F# generic comparer does a lot.
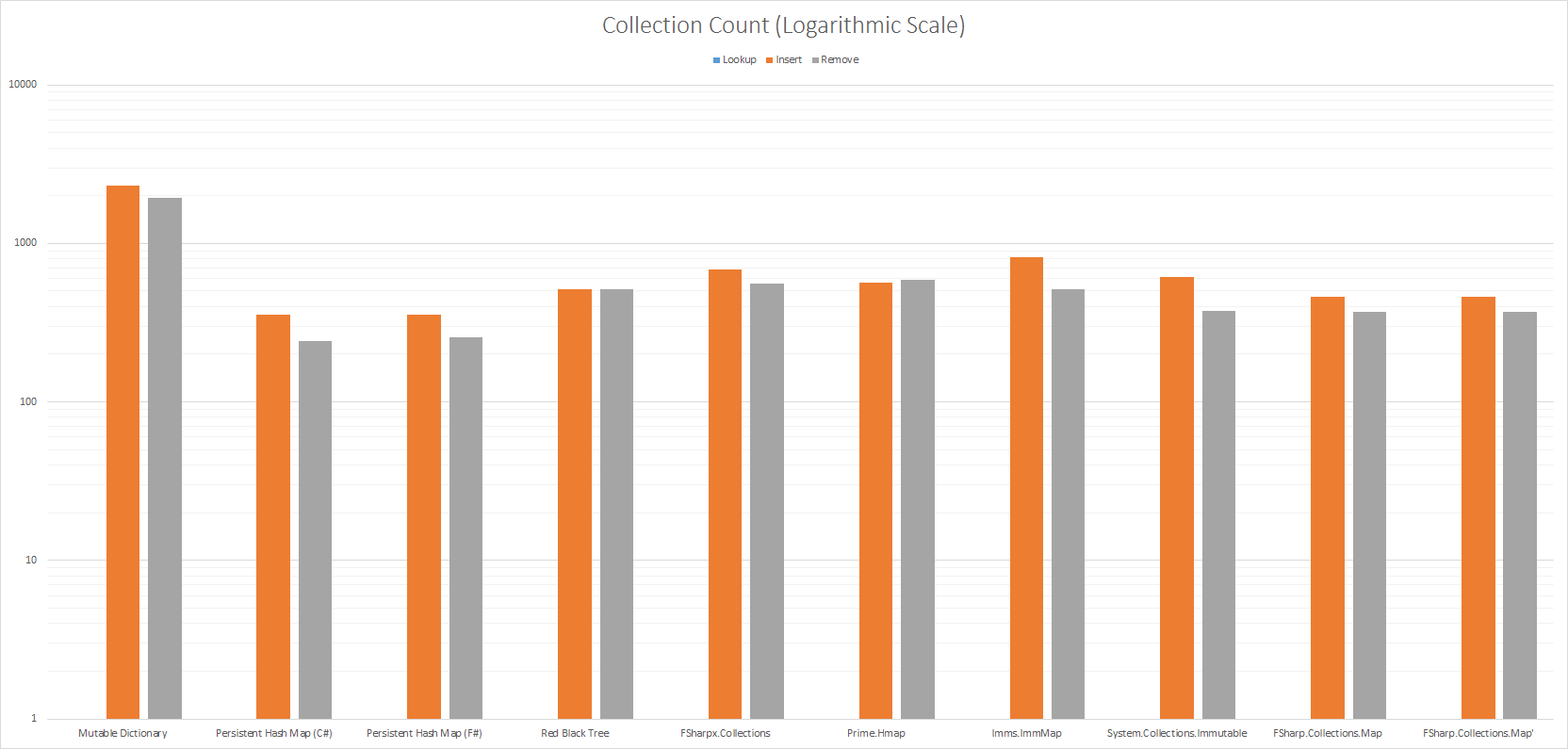
Note the scale on the y-axis is logarithmic to make the collection count comparable.
The number of Garbage Collection that was run during executing gives an estimate of the memory overhead of the various data structures. Lower is better.
System.Collections.Generic.Dictionary<_, _> does poorly because to support immutability a full copy is taken whenever a key is added or removed. If your code can accept destructive updates System.Collections.Generic.Dictionary<_, _> performs a lot better.
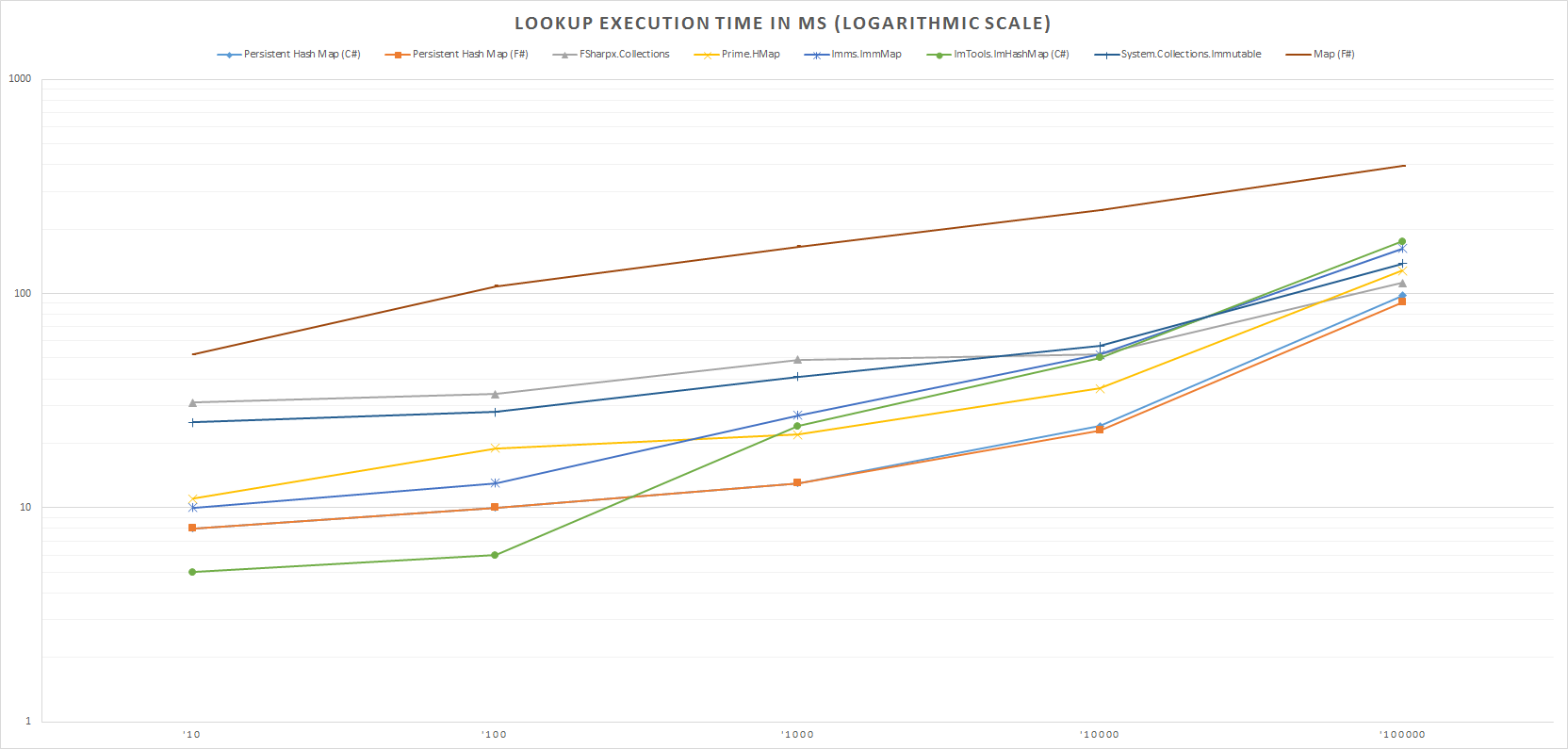
In addition, it's interesting to see the Lookup, Insert and Remove performance depending on the data size.
For these tests I focused on the following algorithms:
- Persistent Hash Map (C#) - "My" Map written in C#
- Persistent Hash Map (F#) - "My" Map written in F#
- FSharpx.Collections.PersistentHashMap
- Prime.Vmap - Anthony Lloyd (@AnthonyLloyd) suggested that I compare against Prime.Vmap
- Imms.ImmMap - Henrik Feldt (@haf) suggested that I compare against Imms.ImmMap
- ImTools.ImHashMap (C#) - Maksim Volkau (@dadhi) submitted a new test case for ImTools
- System.Collections.Immutable.ImmutableDictionary
- FSharp.Collections.Map
The data size varies over 10, 100, 1,000, 10,000 and 100,000 elements but the total work is kept constant to make times comparable.
Note the scale on the y-axis is logarithmic to make the times comparable.
Something I plan to look into is why the performance of "my" maps degrade quicker than others when data size gets close to 100,000 elements.
Note the scale on the y-axis is logarithmic to make the times comparable.
Note the scale on the y-axis is logarithmic to make the times comparable.
It took me a long time and lot of experimentation to find a performant persistent hash map. I am not saying this is the best map out there but it's best I've come up with so far.
During the process I learnt interesting things about the GC and JIT:er during the process which I wanted to share with you during this F# advent.
It turned out that implementing the algorithm in both F# and C# was useful for the process. Occasionally, the C# implementation was the faster which made me reinvestigate the F# code and learning some new tricks in the process. Sometimes it was the other way around. Having competing implementations improved both.
Property Based Testing using FsCheck once again turned out to be awesome to test the properties on the persistent hash map. A persistent hash map does a lot of bit fiddling and FsCheck found many errors during the process for me.
I spent a lot of time disassembling the JIT:ed code. One could wonder how much value there is in that with the advancement in JIT technology. In my personal opinion advancement in JIT happens painfully slow (it's a hard problem) and .NET papers from 2003 still hold up today. I think the learnings drawn from reading JIT:ed code will still be applicable for a long time.
In the end, I am quite satisfied with the final persistent hash map and I hope you found this blog interesting.
I'd like to thank the peer-reviewers:
- Jared Hester (@cloudroutine) for providing me with valuable feedback as well as fixing lot grammatical errors. It seems I am unable to fully master human languages.
- Nicolas Bourbaki (@b0urb4k1) for pointing out several problems with the illustrations as well improving the prose.
Merry F# Christmas,
Mårten Rånge
A hash trie like persistent hash map requires an efficient way to count the number of bits in an integer.
Most CPU:s has special instructions to count the number of set bits, often named popcnt. This is not available to in IL not bytecode so we have to implement it.
A trivial way to count bits is to implement a loop .As long the integer is not 0 check the lowest bit. If it's 1 increment a counter. Shift down the integer.
A slightly better version is to count bits like Peter Wegner (1960):
let popCount v =
let rec loop c v =
if v <> 0u then
loop (c + 1) (v &&& (v - 1u))
else
c
loop 0 vIn FSharpx.Collections a lookup table is used:
let bitCounts =
let bitCounts = Array.create 65536 0
let position1 = ref -1
let position2 = ref -1
for i in 1 .. 65535 do
if !position1 = !position2 then
position1 := 0
position2 := i
bitCounts.[i] <- bitCounts.[!position1] + 1
position1 := !position1 + 1
bitCounts
let inline NumberOfSetBits value =
bitCounts.[value &&& 65535] + bitCounts.[(value >>> 16) &&& 65535]This seems completely reasonable but a problem is that this competes for valuable L1 cache. The bit count cache is 256 KiB in memory which happens to be exactly how much L1 cache my machine has. One can squeeze down the cache to 64 KiB by using byte over int. With some effort one can make the cache 32 KiB.
On my machine a cold read from main memory under semi-high load is about 100ns about 340 clock cycles. This is an eternity.
Instead one can use a parallel bit counting algorithm like below:
let inline popCount i =
let mutable v = i
v <- v - ((v >>> 1) &&& 0x55555555u)
v <- (v &&& 0x33333333u) + ((v >>> 2) &&& 0x33333333u)
((v + (v >>> 4) &&& 0xF0F0F0Fu) * 0x1010101u) >>> 24This is parallel bit counting algorithm taken from the wonderful resource on Bit Twiddling Hacks. For more info see Hamming weights on Wikipedia.
The algorithms. Because the lookup based algorithm performance is heavily dependent on cache locality getting true numbers is very difficult but we can estimate worst-case by checking the assembly code and measuring the best-case.
The JIT:ed parallel popCount looks like this:
00007FF815560C9C mov eax,esi
00007FF815560C9E shr eax,1
00007FF815560CA0 and eax,55555555h
00007FF815560CA5 mov edx,esi
00007FF815560CA7 sub edx,eax
00007FF815560CA9 mov eax,edx
00007FF815560CAB mov edx,eax
00007FF815560CAD and edx,33333333h
00007FF815560CB3 shr eax,2
00007FF815560CB6 and eax,33333333h
00007FF815560CBB add eax,edx
00007FF815560CBD mov edx,eax
00007FF815560CBF shr edx,4
00007FF815560CC2 add eax,edx
00007FF815560CC4 and eax,0F0F0F0Fh
00007FF815560CC9 imul eax,eax,1010101h
00007FF815560CCF shr eax,18hIt almost looks like the F# code! As the operations are just on registers this should perform fast and not suffer from potential cache misses.
The JIT:ed lookup based code looks like this:
; Loads the reference to the lookup table into rax
00007FF815590C1C mov rax,1276F6A59D8h
; Loads the address of the lookup table into rax
00007FF815590C26 mov rax,qword ptr [rax]
; Loads the size of the lookup table into edx
00007FF815590C29 mov edx,dword ptr [rax+8]
; Keep the lower 16 bits
00007FF815590C2C mov ecx,esi
00007FF815590C2E and ecx,0FFFFh
; Checks if we are out of bounds
00007FF815590C34 cmp ecx,edx
00007FF815590C36 jae 00007FF815590C6F
00007FF815590C38 movsxd rdx,ecx
; Loads the bit count for the lower 16 bits into eax
00007FF815590C3B mov eax,dword ptr [rax+rdx*4+10h]
; Loads the reference to the lookup table into rdx
00007FF815590C3F mov rdx,1276F6A59D8h
; Loads the address of the lookup table into rdx
00007FF815590C49 mov rdx,qword ptr [rdx]
; Keep the upper 16 bits
00007FF815590C4C mov ecx,esi
00007FF815590C4E sar ecx,10h
00007FF815590C51 and ecx,0FFFFh
; Loads the size of the lookup table into r8d
00007FF815590C57 mov r8d,dword ptr [rdx+8]
; Checks if we are out of bounds
00007FF815590C5B cmp ecx,r8d
00007FF815590C5E jae 00007FF815590C6F
00007FF815590C60 movsxd rcx,ecx
; Loads the bit count for the lower 16 bits into eax
00007FF815590C63 mov edx,dword ptr [rdx+rcx*4+10h]
; Adds the two bitcounts for final result
00007FF815590C67 add eax,edxThe lookup based code has more instructions than the parallel bit count. In addition, it has to reads from memory which in worst case might result in a full cache miss taking up to ~700 cycles.
So it looks like worst case (for the lookup table algorithm) the parallel algorithm should perform a lot better as well as not occupying valuable L1 cache.
We can measure the best case performance by running a performance test on both algorithms. The reason this yield best case performance is that since we are just calling the algorithms over and over again we should have basically no cache misses.
On my machine the numbers are:
- 2.7 seconds for the lookup based algorithm
- 2.2 seconds for the parallel bit count algorithm
With these numbers in mind as well as the minimal usage of L1 cache I think parallel bit counting is preferable to lookup tables.
As an old Atari/Amiga programmer this hurts because lookup tables were the goto solutions for any problem. But that was before computers had caches. On modern computers, it seems the old tricks of the trade no longer work.
F# Map performs poorly but the root cause seems to be that Map relies on GenericCompare in FSharp.Core to compare keys.
prim-types.fs:
/// Implements generic comparison between two objects. This corresponds to the pseudo-code in the F#
/// specification. The treatment of NaNs is governed by "comp".
let rec GenericCompare (comp:GenericComparer) (xobj:obj,yobj:obj) = ...F# has some smart tricks up its sleeve to select the fastest comparer for a type that supports the comparison constraint. However, those tricks only applies to inline methods. For Map F# falls back on GenericCompare.
The issue is that for Map<K, V> the key-type is often a sealed type, like string, yet the way GenericCompare works is that it does several type tests until it actually compared the values. For the Key type in the performance tests I counted to 12 type tests before it lands in CompareTo.
As Map is a balanced tree it needs to compare the key at each level until it finds the result. If the tree is 12 levels deep GenericCompare does 144 type tests. For most key types 144 unnecessary type tests. This explains the surprising result that Lookup is as slow as Insert for Map. For all other data structures Lookup is faster.
As an experiment, I exposed a method that allows the program to specify a custom comparer for a Map. That improved performance of Lookup for Map by an order of magnitude.
There are good reasons to not allow custom comparers for Map as mixing Maps with different comparers could give unpredictable results.
If a custom comparer is out of the picture the alternative is optimizing GenericCompare but as this is a core part of F# it's also very risky.
It seems that there are never any easy answers.
A persistent hash map requires the ability to test for equality and we have the choice of equality vs IEquatable<_>. Is there a performance issue for equality as well.
I built a program to compare performance:
type [<Sealed>] Key(v : int) =
member x.Value = v
interface IComparable with
member x.CompareTo(o : obj) =
match o with
| :? Key as k -> v.CompareTo (k.Value)
| _ -> -1
interface IComparable<Key> with
member x.CompareTo(o : Key) = v.CompareTo (o.Value)
interface IEquatable<Key> with
member x.Equals(o : Key) = v = o.Value
override x.Equals(o : obj) =
match o with
| :? Key as k -> v = k.Value
| _ -> false
override x.GetHashCode() = v.GetHashCode ()
override x.ToString() = sprintf "%d" v
let makeKey i = Key i
let equality l r = l = r
let equatable<'T when 'T :> IEquatable<'T>> (l : 'T) (r : ' T) = l.Equals r
let comparison l r = l < r
let comparable<'T when 'T :> IComparable<'T>> (l : 'T) (r : ' T) = l.CompareTo r > 0The performance numbers are:
Equality: (false, 254L, 0, 0, 0)
Equatable: (false, 41L, 0, 0, 0)
Comparison: (true, 396L, 0, 0, 0)
Comparable: (false, 49L, 0, 0, 0)
It seems from this test that comparison is ~8x slower than IComparable<_> for types that support fast comparison.
equality seems to be ~6x slower than IEquatable for types that support fast equality comparison.
A persistent hash map is less susceptible than Map to slow comparisons as the persistent hash doesn't compare the keys until it reached the leaf.
But as the whole point of this exercise is to build the best persistent hash map I can, I decided that the key type needs to implement IEquatable<_> for performance reasons.
I used a base class for the persistent hash map but typically in F# we rely on ADT for these kinds of problems.
However, performance measurements showed me that test-then-cast used by F# pattern matching is more expensive than virtual dispatch. It also turns out that calling interface methods takes more time than call abstract methods.
To understand we define a simple base class:
[<AbstractClass>]
type Base() =
abstract Value : int
let w =
{ new Base() with
override x.Value = 3
}The JIT:ed code for w.Value looks like this:
; Loads this pointer into rcx
00007ffe`895a04f0 488b09 mov rcx,qword ptr [rcx]
; Loads MethodTable into rax
00007ffe`895a04f3 488b01 mov rax,qword ptr [rcx]
; Loads vtable into rax
00007ffe`895a04f6 488b4040 mov rax,qword ptr [rax+40h]
; Virtual Dispatch Value method
00007ffe`895a04fa ff5020 call qword ptr [rax+20h]This looks like a quite "normal" way (ie like C++ does it) to do virtual dispatch through vtables and should be reasonable effective.
Let's compare to virtual dispatch through an interface:
type IA =
interface
abstract member Value: int
end
let v =
{ new IA with
override x.Value = 2
}The JIT:ed code for v.Value looks like this:
; Loads this pointer into rcx
00007ffe`895a04d2 488b09 mov rcx,qword ptr [rcx]
; ???
00007ffe`895a04d5 49bb20004a89fe7f0000 mov r11,7FFE894A0020h
; ???
00007ffe`895a04df 3909 cmp dword ptr [rcx],ecx
00007ffe`895a04e1 41ff13 call qword ptr [r11]This code confused me a lot. What is r11? Why the compare? It turns out that in .NET there's only one vtable per object, probably a design decision inherited from JRE. To support multiple interfaces per object a bit more work must be done to locate the correct method. When one follows the calls, it turns out that the base class virtual dispatch ends up in the overloaded method but for interface virtual dispatch we end up in a helper function that looks up the interface method in a table. Therefore, interface virtual dispatch is slower than base class virtual dispatch.
Finally let's look at "virtual dispatch" for ADT:s.
type ADT =
| First of int
| Second of int
| Third of int
| Fourth of int
| Fifth of int
member x.Value =
match x with
| First v -> v
| Second v -> v
| Third v -> v
| Fourth v -> v
| Fifth v -> v
let u = First 1To understand the JIT:ed code it's worth knowing that F# implements ADT:s using a base class that the union cases inherit from. The decompiled pattern match code for x.Value looks like this:
public int Value
{
get
{
switch (this.Tag)
{
case 0:
IL_1F:
return ((Program.ADT.First)this).item;
case 1:
return ((Program.ADT.Second)this).item;
case 2:
return ((Program.ADT.Third)this).item;
case 3:
return ((Program.ADT.Fourth)this).item;
case 4:
return ((Program.ADT.Fifth)this).item;
}
goto IL_1F;
}
}This helps understanding the JIT:ed code for u.Value:
; Loads this.Tag into ecx
00007ffe`895b06de 8b4e08 mov ecx,dword ptr [rsi+8] ds:000001c3`5e4844d0=00000000
00007ffe`895b06e1 4863c9 movsxd rcx,ecx
; Are we in range?
; Unnecessary because you can't extend ADTs
00007ffe`895b06e4 4883f904 cmp rcx,4
; If no then attempt to cast to `First`, this throw an exception
00007ffe`895b06e8 7716 ja 00007ffe`895b0700
; Switches are implemented using a lookup table of jump address
00007ffe`895b06ea 488d15df000000 lea rdx,[00007ffe`895b07d0]
00007ffe`895b06f1 8b148a mov edx,dword ptr [rdx+rcx*4]
00007ffe`895b06f4 488d05deffffff lea rax,[00007ffe`895b06d9]
00007ffe`895b06fb 4803d0 add rdx,rax
; Jump to the case
00007ffe`895b06fe ffe2 jmp rdx
; Case 0, the tag indicated x is a union case First
00007ffe`895b0700 488bfe mov rdi,rsi
; Attempting to cast to First
; Check for null pointer
; Unnecessary because we already dereferenced this pointer earlier but the JIT:er failed to see it
; If null then the cast succeeds a we proceed (which will throw when we try to dereference)
00007ffe`895b0703 4885ff test rdi,rdi
00007ffe`895b0706 741a je 00007ffe`895b0722
; Do a quick check if we are casting to the most derived type
; Unnecessary because we always are but the JIT:er failed to see it
00007ffe`895b0708 48b9e08a4a89fe7f0000 mov rcx,7FFE894A8AE0h
00007ffe`895b0712 48390f cmp qword ptr [rdi],rcx
00007ffe`895b0715 740b je 00007ffe`895b0722
; If not most derived type we have to do a more extensive check
; Meaning casting to non most derived types are more expensive
00007ffe`895b0717 488bd6 mov rdx,rsi
00007ffe`895b071a e80135605f call clr!JIT_ChkCastClassSpecial (00007ffe`e8bb3c20)
00007ffe`895b071f 488bf8 mov rdi,rax
; Loads v into eax
00007ffe`895b0722 8b460c mov eax,dword ptr [rsi+0Ch]
; We are done, bail out
00007ffe`895b0725 e99a000000 jmp 00007ffe`895b07c4
; Case 1, the tag indicated x is a union case Second
00007ffe`895b072a 488bfe mov rdi,rsi
00007ffe`895b072d 4885ff test rdi,rdi
00007ffe`895b0730 741a je 00007ffe`895b074cIf we remove all unnecessary checking the code could look something like this:
; Loads this.Tag into ecx
00007ffe`895b06de 8b4e08 mov ecx,dword ptr [rsi+8] ds:000001c3`5e4844d0=00000000
00007ffe`895b06e1 4863c9 movsxd rcx,ecx
; Switches are implemented using a lookup table of jump address
00007ffe`895b06ea 488d15df000000 lea rdx,[00007ffe`895b07d0]
00007ffe`895b06f1 8b148a mov edx,dword ptr [rdx+rcx*4]
00007ffe`895b06f4 488d05deffffff lea rax,[00007ffe`895b06d9]
00007ffe`895b06fb 4803d0 add rdx,rax
; Jump to the case
00007ffe`895b06fe ffe2 jmp rdx
; Case 0, the tag indicated x is a union case First
00007ffe`895b0722 8b460c mov eax,dword ptr [rsi+0Ch]
00007ffe`895b0725 e99a000000 jmp 00007ffe`895b07c4
; Case 1, the tag indicated x is a union case Second
00007ffe`895b0722 8b460c mov eax,dword ptr [rsi+0Ch]
00007ffe`895b0725 e99a000000 jmp 00007ffe`895b07c4If the JIT:er could eliminate all unnecessary checks, the performance of ADT "virtual dispatch" would be comparable to virtual dispatch to base classes. The lookup method could then be implemented tail recursively which means it's possible that ADT:s could be the fastest way to implement a persistent hash map. As it looks today virtual dispatch through a base class seems to be the fastest option.
A core part of the path copying is copying the array of sub nodes. We need not just a plain array copy, but also a copy while making room for a new node, as well as a copy while removing a node.
The functions look like this:
let inline copyArray (vs : 'T []) : 'T [] =
let nvs = Array.zeroCreate vs.Length
System.Array.Copy (vs, nvs, vs.Length)
nvs
let inline copyArrayMakeHoleLast (peg : 'T) (vs : 'T []) : 'T [] =
let nvs = Array.zeroCreate (vs.Length + 1)
System.Array.Copy (vs, nvs, vs.Length)
nvs.[vs.Length] <- peg
nvs
let inline copyArrayMakeHole (at : int) (peg : 'T) (vs : 'T []) : 'T [] =
let nvs = Array.zeroCreate (vs.Length + 1)
System.Array.Copy (vs, nvs, at)
System.Array.Copy (vs, at, nvs, at + 1, vs.Length - at)
nvs.[at] <- peg
nvs
let inline copyArrayRemoveHole (at : int) (vs : 'T []) : 'T [] =
let nvs = Array.zeroCreate (vs.Length - 1)
System.Array.Copy (vs, nvs, at)
System.Array.Copy (vs, at + 1, nvs, at, vs.Length - at - 1)
nvsAn early attempt of these functions used normal loops to copy an array. My reasoning was that invoking a function does have some cost, but it'd probably be cheaper if I just copied them by hand.
I was extremely wrong in this assumption. Performance tests showed that insert/removal performance was doubled with System.Array.Copy and considering that the functions do other stuff than just copy arrays the overhead must be huge.
What I couldn't understand was why. This is when I started to read up on the card table in .NET GC.
The GC in .NET is generational GC meaning that the GC runs frequent cleans of Gen0 objects ie newly created objects. Objects that survive are promoted to Gen1 and may be promoted to Gen2 in turn.
Gen2 objects are collected with by a full GC. A full GC is expensive which is why we have different generations of objects so that we may run smaller less costly GC on just Gen0 objects.
When a Gen0 collect is started the GC follows the root references (like variables on the stack or global references). When a Gen1 or Gen2 object is detected they are assumed to be alive and the GC stops following the that branch. For Gen0 objects the full graph is followed and all seen objects are marked as survivors and promoted to Gen1. The other objects are collected.
Brilliant but there's just one small problem. What if you created a new object in Gen0 and updated a Gen2 object to "point" to that object? The new object must not be collected in this case!
To support that whenever a reference field in an object is changed something called a card table is updated as well. You can imagine a card-table as a set of bits where each bit represents a changed object. Whenever an object is changed the corresponding bit is set. Then during collect the bit set is traversed and for each object that has had its bit set in the card table its references are followed as if they were root references. That way the Gen0 object that the Gen2 object points to will not be collected.
Great and this also explains why my attempt to write loops to copy the nodes was much slower than System.Array.Copy. After each copied element, the JIT:er automatically inserts a call to JIT_WriteBarrier which updates the card table for the array I copied to. System.Array.Copy is optimized so that all nodes are copied and then at the end JIT_WriteBarrier is called once.
It's "easily" seen that this is happening when we examine the JIT:ed assembly code of this simple function:
let f (vs : _ []) =
let vvs = Array.zeroCreate vs.Length
let rec loop i =
if i < vvs.Length then
vvs.[i] <- vs.[i]
loop (i + 1)
loop 0
vvsThe relevant x64 code:
; if i < vvs.Length then
00007ffb`0ff10a3c 397708 cmp dword ptr [rdi+8],esi
00007ffb`0ff10a3f 7e1f jle 00007ffb`0ff10a60
00007ffb`0ff10a41 448b4308 mov r8d,dword ptr [rbx+8]
; Out of range check for vs
00007ffb`0ff10a45 413bf0 cmp esi,r8d
00007ffb`0ff10a48 731e jae 00007ffb`0ff10a68
00007ffb`0ff10a4a 4c63c6 movsxd r8,esi
; let tmp = vs.[i] // Reading from the source array
00007ffb`0ff10a4d 4e8b44c310 mov r8,qword ptr [rbx+r8*8+10h]
00007ffb`0ff10a52 488bcf mov rcx,rdi
00007ffb`0ff10a55 8bd6 mov edx,esi
; vvs.[i] <- tmp // Assigning to the destination array
00007ffb`0ff10a57 e82435615f call clr!JIT_Stelem_Ref (00007ffb`6f523f80)
00007ffb`0ff10a5c ffc6 inc esi
00007ffb`0ff10a5e ebd0 jmp 00007ffb`0ff10a3cLet's look at clr!JIT_Stelem_Ref:
; Is array reference null?
00007ffb`6f523f80 4885c9 test rcx,rcx
00007ffb`6f523f83 7436 je clr!JIT_Stelem_Ref+0x3b (00007ffb`6f523fbb)
00007ffb`6f523f85 0bd2 or edx,edx
; Is array index out of bounds?
00007ffb`6f523f87 3b5108 cmp edx,dword ptr [rcx+8]
00007ffb`6f523f8a 733b jae clr!JIT_Stelem_Ref+0x47 (00007ffb`6f523fc7)
00007ffb`6f523f8c 4c8b11 mov r10,qword ptr [rcx]
; Are we assigning a null reference?
00007ffb`6f523f8f 4d85c0 test r8,r8
00007ffb`6f523f92 7416 je clr!JIT_Stelem_Ref+0x2a (00007ffb`6f523faa)
00007ffb`6f523f94 4d8b4a30 mov r9,qword ptr [r10+30h]
; Is the type of object compatible with the array?
00007ffb`6f523f98 4d3b08 cmp r9,qword ptr [r8]
00007ffb`6f523f9b 7513 jne clr!JIT_Stelem_Ref+0x30 (00007ffb`6f523fb0)
00007ffb`6f523f9d 488d4cd110 lea rcx,[rcx+rdx*8+10h]
00007ffb`6f523fa2 498bd0 mov rdx,r8
; Call to the infamous JIT_WriteBarrier! This writes the non-null value and updates the card table
; Since it's a jmp the ret from clr!JIT_WriteBarrier will return the caller of clr!JIT_Stelem_Ref
00007ffb`6f523fa5 e986feffff jmp clr!JIT_WriteBarrier (00007ffb`6f523e30)
; Writes the null value to the array, no need to update card table
00007ffb`6f523faa 4c8944d110 mov qword ptr [rcx+rdx*8+10h],r8
00007ffb`6f523faf c3 retAs this calls clr!JIT_WriteBarrier let's look at that function as well.
; Updates the reference
00007ffb`6f523e30 488911 mov qword ptr [rcx],rdx
00007ffb`6f523e33 0f1f00 nop dword ptr [rax]
; Loads Gen2 boundary
00007ffb`6f523e36 48b81810e0a6d5010000 mov rax,1D5A6E01018h
; If it's a Gen2 object we bail out
00007ffb`6f523e40 483bd0 cmp rdx,rax
00007ffb`6f523e43 722b jb clr!JIT_WriteBarrier+0x40 (00007ffb`6f523e70)
00007ffb`6f523e45 90 nop
; Loads address to card table
00007ffb`6f523e46 48b840242b84d5010000 mov rax,1D5842B2440h
; Divide this pointer with 2048
00007ffb`6f523e50 48c1e90b shr rcx,0Bh
; Is the flag set?
00007ffb`6f523e54 803c08ff cmp byte ptr [rax+rcx],0FFh
00007ffb`6f523e58 7502 jne clr!JIT_WriteBarrier+0x2c (00007ffb`6f523e5c)
00007ffb`6f523e5a f3c3 rep ret
; No, then set it. The check-then-set pattern avoids cache synchronization
00007ffb`6f523e5c c60408ff mov byte ptr [rax+rcx],0FFh
00007ffb`6f523e60 c3 ret
00007ffb`6f523e61 666666666666660f1f840000000000 nop word ptr [rax+rax]
00007ffb`6f523e70 f3c3 rep ret
00007ffb`6f523e72 6666666666660f1f840000000000 nop word ptr [rax+rax]
00007ffb`6f523e80 f3c3 rep retAs we can see, there's quite a lot of computation that happens for each array assignment. The problem is that the JIT:er sees each assignment individually and therefore can't figure out that several checks are performed unnecessarily.
The implementer of System.Array.Copy can use a priori knowledge on how arrays works to eliminate unnecessary checks and calls to JIT_WriteBarrier.
Note that we update a value type field or an value type array element there will be no call JIT_WriteBarrier as value types aren't GC:ed.
So for the future it can be good to keep in mind that while updating reference fields this will also insert an "invisible" call to JIT_WriteBarrier which may or may not have significant performance impact.


Great post!
Have you seen Vmap (https://github.com/bryanedds/Nu/tree/master/Prime)? It would be interesting to compare it.