The entry point best_multiexp parallelize by splitting the number of points.
However MSM scales with O(n log n) i.e. the more points we have, the less costly adding them is.
So splitting by the number of points should be last resort.
The current implementation multiexp_serial is the baseline MSM using bucket algorithm as described in
- Faster batch forgery identification Daniel J. Bernstein, Jeroen Doumen, Tanja Lange, and Jan-Jaap Oosterwijk, 2012 https://eprint.iacr.org/2012/549.pdf
- Simple guide to fast linear combinations (aka multiexponentiations) Vitalik Buterin, 2020 https://ethresear.ch/t/simple-guide-to-fast-linear-combinations-aka-multiexponentiations/7238 https://github.com/ethereum/research/blob/5c6fec6/fast_linear_combinations/multicombs.py
- zkStudyClub: Multi-scalar multiplication: state of the art & new ideas Gus Gutoski, 2020 https://www.youtube.com/watch?v=Bl5mQA7UL2I
i.e. no specific comment, it’s within 2x of the best serial implementations.
privacy-scaling-explorations/halo2#40
This implementation follows Barretenberg technique to allow affine “vector additions” i.e. we find N points going into N buckets and we do N independent sums.
Field arithmetic costs:
- M = Multiplication
- S = Squaring, usually 0.8M to 1M, likely 1M for BN254)
- I = Inversion, usually 70M to 100M depending on the number of bits and the inversion strategy
- Inversion using Fermat’s Little theorem a⁻¹ ≡ aᵖ⁻² (mod p) is quadratic in the number of bits
- Inversion using the extended Euclidean algorithm is linear in the number of bits
A technique called “Montgomery’s batch inversion” can transform n inversions nI into 3n*M + I
Elliptic curve arithmetic can be done in many coordinate systems. The canonical system, affine coordinates, is usually avoided because the cost is 3M+I compared to 7M+4S (Jacobian + affine) or 11M+5S (Jacobian+Jacobian), see formula database https://www.hyperelliptic.org/EFD/g1p/auto-shortw-jacobian-0.html.
However with many independent points we can use Montgomery’s batch inversion to amortize the cost of inversion over n EC additions, for an asymptotic cost per addition of 6M + I/n
Hence Barrentenberg is asymptotically 1.83x faster than the baseline implementation.
The implementation of Barretenberg and in PR #40 however suffers from memory bottlenecks and unnecessary complexity.
Size of c / k / w window size
See https://github.com/privacy-scaling-explorations/halo2/pull/40/files#diff-1f545e0039677113517c7970d2a49ef844e6e01375debfa994cceda8e0854dedR971-R1007 to determine the best size.
A formula that returns the number of operations is available at:
- zkStudyClub: Multi-scalar multiplication: state of the art & new ideas Gus Gutoski, 2020 https://www.youtube.com/watch?v=Bl5mQA7UL2I does not take signed digits into account
- https://github.com/dalek-cryptography/curve25519-dalek/blob/618c508/src/backend/serial/scalar_mul/pippenger.rs#L46-L54 does not take signed digits into account
- A tuned formula used for dispatching in Constantine https://github.com/mratsim/constantine/blob/0eba593/constantine/math/elliptic/ec_multi_scalar_mul_scheduler.nim#L164-L213
func bestBucketBitSize*(inputSize: int, scalarBitwidth: static int, useSignedBuckets, useManualTuning: static bool): int {.inline.} =
## Evaluate the best bucket bit-size for the input size.
## That bucket size minimize group operations.
## This ignore cache effect. Computation can become memory-bound, especially with large buckets
## that don't fit in L1 cache, trigger the 64K aliasing conflict or worse (overflowing L2 cache or TLB).
## Especially, scalars are expected to be indistinguishable from random so buckets accessed during accumulation
## will be in a random pattern, triggering cache misses.
# Raw operation cost is approximately
# 1. Bucket accumulation
# n - (2ᶜ-1) additions for b/c windows or n - (2ᶜ⁻¹-1) if using signed buckets
# 2. Bucket reduction
# 2x(2ᶜ-2) additions for b/c windows or 2*(2ᶜ⁻¹-2)
# 3. Final reduction
# (b/c - 1) x (c doublings + 1 addition)
# Total
# b/c (n + 2ᶜ - 2) A + (b/c - 1) * (c*D + A)
# https://www.youtube.com/watch?v=Bl5mQA7UL2I
# A doubling costs 50% of an addition with jacobian coordinates
# and between 60% (BLS12-381 G1) to 66% (BN254-Snarks G1)
const A = 10'f32 # Addition cost
const D = 6'f32 # Doubling cost
const s = int useSignedBuckets
let n = inputSize
let b = float32(scalarBitwidth)
var minCost = float32(Inf)
for c in 2 .. 20: # cap return value at 17 after manual tuning
let b_over_c = b/c.float32
let bucket_accumulate_reduce = b_over_c * float32(n + (1 shl (c-s)) - 2) * A
let final_reduction = (b_over_c - 1'f32) * (c.float32*D + A)
let cost = bucket_accumulate_reduce + final_reduction
if cost < minCost:
minCost = cost
result = c
# Manual tuning, memory bandwidth / cache boundaries of
# L1, L2 caches, TLB and 64 aliasing conflict
# are not taken into account in previous formula.
# Each increase in c doubles memory used.
when useManualTuning:
if 14 <= result:
result -= 1
if 15 <= result:
result -= 1
if 16 <= result:
result -= 1With
- A = EC addition
- D = EC doubling
- b the number of scalar bits (254)
- n the number of points,
the total operation cost is: b/c (n + 2ᶜ - 2) A + (b/c - 1) * (c*D + A)
and c is about log₂(n) so that MSM has an asymptotic complexity of O(n log₂ n).
However, this theoretical operation cost analysis ignores:
-
crossing the L1, L2 and TLB cache boundaries:
-
See http://igoro.com/archive/gallery-of-processor-cache-effects/ for looping over an array
-
See https://www.hpl.hp.com/techreports/93/HPL-93-89.pdf for effect on bit-reversal permutation (an FFT-related data reordering)
-
-
The 4K aliasing issue https://cdrdv2.intel.com/v1/dl/getContent/671488?explicitVersion=true
-
The 64K aliasing conflict https://qcd.phys.cmu.edu/QCDcluster/intel/vtune/reference/64k_Aliasing_Conflicts.htm
This event counts the number of 64K-aliasing conflicts. A 64K-aliasing conflict occurs when a virtual address memory references a cache line that is modulo 64K bytes apart from another cache line that already resides in the first level cache. Only one cache line with a virtual address modulo 64K bytes can reside in the first level cache at the same time.
For example, accessing a byte at virtual addresses 0x10000 and 0x3000F would cause a 64K aliasing conflict. This is because the virtual addresses for the two bytes reside on cache lines that are modulo 64K bytes apart.
On the Intel Pentium 4 and Intel Xeon processors with CPUID signature of family encoding 15, model encoding of 0, 1 or 2, the 64K aliasing conflict also occurs when addresses have identical value in bits 15:6. If you avoid this kind of aliasing, you can speedup programs by a factor of three if they load frequently from preceding stores with aliased addresses and there is little other instruction-level parallelism available. The gain is smaller when loads alias with other loads, which cause thrashing in the first-level cache.
Note: while Pentium 4 are particularly affected, this also affects current CPUs.
The more buckets we have, the more likely these memory effects crops up. This is verified in practice and over 2¹⁶ buckets memory bottlenecks become very noticeable.
This also has an implication on endomorphism acceleration and parallelism strategy as we will see later.
The baseline implementation uses log(n): https://github.com/privacy-scaling-explorations/halo2/blob/a764a7f/halo2_proofs/src/arithmetic.rs#L31-L37 (inherited from libsnarks).
The PR uses an empirical values derived from benches: https://github.com/privacy-scaling-explorations/halo2/pull/40/files#diff-1f545e0039677113517c7970d2a49ef844e6e01375debfa994cceda8e0854dedR103-R118
/// Returns the best bucket width for the given number of points.
fn get_best_c(num_points: usize) -> usize {
if num_points >= 262144 {
15
} else if num_points >= 65536 {
12
} else if num_points >= 16384 {
11
} else if num_points >= 8192 {
10
} else if num_points >= 1024 {
9
} else {
7
}
}Recommendation: see endomorphism acceleration section, get_best_c will need to be refined when endomorphism acceleration actually slow downs MSM.
Signed digit representation
Classic scalar multiplication uses the double-and-add algorithm, with w the window size and dᵢ the digit of size w bits at position i:
Q ← 0
for i from m to 0 do
Q ← point_double_repeat(Q, w)
if dᵢ > 0 then
Q ← point_add(Q, dᵢP) # using pre-computed value of dᵢP
elif dᵢ < 0 then
Q ← point_sub(Q, dᵢP)
else
discard
return QThe PR uses wNAF (windowed NAF) for signed digit representation.
- The main appeal of windowed NAF is reducing the average Hamming Weight of random scalar from 1/2 (random) to 1/3 (NAF) or even less depending on window size. Meaning there are more zeros so we skip additions.
- The second benefit is due to the sign which allows dividing by 2 the precomputed table requirement. Hence a window of size 5 would need 2⁴ = 16 elements instead of 32 if unsigned.
However the main appeal of window NAF is not applicable to MSM because as your window grow, it’s exponentially more likely that at least a bit is set and you will have an addition anyway:
/// Performs a small multi-exponentiation operation.
/// Uses the double-and-add algorithm with doublings shared across points.
pub fn small_multiexp<C: CurveAffine>(coeffs: &[C::Scalar], bases: &[C]) -> C::Curve {
let coeffs: Vec<_> = coeffs.iter().map(|a| a.to_repr()).collect();
let mut acc = C::Curve::identity();
// for byte idx
for byte_idx in (0..32).rev() {
// for bit idx
for bit_idx in (0..8).rev() {
acc = acc.double();
// for each coeff
for coeff_idx in 0..coeffs.len() {
let byte = coeffs[coeff_idx].as_ref()[byte_idx];
if ((byte >> bit_idx) & 1) != 0 {
acc += bases[coeff_idx];
}
}
}
}
acc
}Regarding the disadvantages of wNAF, you need:
-
Transformation of all scalars/coefficients to wNAF ahead of time as wNAF needs to propagate a carry and look at the whole scalar: https://github.com/privacy-scaling-explorations/halo2/pull/40/files#diff-1f545e0039677113517c7970d2a49ef844e6e01375debfa994cceda8e0854dedR79-R101
-
This transformation requires extra memory, for 1M 254-bit scalar that’s 32MB. That’s more cache miss in a critical path
-
It diminishes parallelism opportunities due to the carry dependency, this is particularly problematic on GPU with thousands of cores
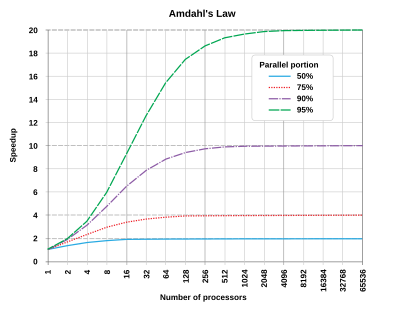
See also Amdahl’s Law: https://en.wikipedia.org/wiki/Amdahl%27s_law
There is however a signed representation that is not optimal (but we don’t care about this property) but can be computed on-the-fly without extra allocation:
- Booth encoding https://en.wikipedia.org/wiki/Booth%27s_multiplication_algorithm
- Implementation to get signed windows on-the-fly: https://github.com/mratsim/constantine/blob/0eba593/constantine/math/arithmetic/bigints.nim#L792-L847
Recommendation: switch to Booth encoding to avoid intermediate allocation and improve parallelism opportunities
Endomorphism acceleration
In my experiments, endomorphism acceleration starts having too much overhead when buckets reach 2¹³ to 2¹⁴ in number of points. This can be explain by the overhead of:
- Allocating large memory (the allocator will have to mmap and mmap is slow)
- Computing the mini-scalars
- Memory bottlenecks
While the gain in operation count between
- 254/13 = 19.5 mini-MSMs (no endomorphisms)
- and 128/13 = 9.85 mini-MSMs (with endomorphisms)
is only about 2x and does not overcome the bottleneck.
Recommendation: benchmark when endomorphism acceleration results in a slowdown
Architecture to enable batch affine
The architecture to enable batch affine is complex and hard to maintain, see the support data structure: https://github.com/privacy-scaling-explorations/halo2/pull/40/files#diff-1f545e0039677113517c7970d2a49ef844e6e01375debfa994cceda8e0854dedR127-R187
/// MultiExp context object
#[derive(Clone, Debug, Default)]
pub struct MultiExpContext<C: CurveAffine> {
/// Memory to store the points in the addition tree
points: Vec<C>,
/// Memory to store wnafs
wnafs: Vec<u32>,
/// Memory split up between rounds
rounds: SharedRoundData,
}
/// SharedRoundData
#[derive(Clone, Debug, Default)]
struct SharedRoundData {
/// Memory to store bucket sizes
bucket_sizes: Vec<usize>,
/// Memory to store bucket offsets
bucket_offsets: Vec<usize>,
/// Memory to store the point data
point_data: Vec<u32>,
/// Memory to store the output indices
output_indices: Vec<u32>,
/// Memory to store the base positions (on the first level)
base_positions: Vec<u32>,
/// Memory to store the scatter maps
scatter_map: Vec<ScatterData>,
}
/// RoundData
#[derive(Debug, Default)]
struct RoundData<'a> {
/// Number of levels in the addition tree
pub num_levels: usize,
/// The length of each level in the addition tree
pub level_sizes: Vec<usize>,
/// The offset to each level in the addition tree
pub level_offset: Vec<usize>,
/// The size of each bucket
pub bucket_sizes: &'a mut [usize],
/// The offset of each bucket
pub bucket_offsets: &'a mut [usize],
/// The point to use for each coefficient
pub point_data: &'a mut [u32],
/// The output index in the point array for each pair addition
pub output_indices: &'a mut [u32],
/// The point to use on the first level in the addition tree
pub base_positions: &'a mut [u32],
/// List of points that are scattered to the addition tree
pub scatter_map: &'a mut [ScatterData],
/// The length of scatter_map
pub scatter_map_len: usize,
}
/// ScatterData
#[derive(Default, Debug, Clone)]
struct ScatterData {
/// The position in the addition tree to store the point
pub position: u32,
/// The point to write
pub point_data: u32,
}Writeup: https://github.com/AztecProtocol/barretenberg/blob/871cf65/cpp/src/barretenberg/ecc/pippenger.md
We can add a preprocessing step that organises our point data into 'bucket order'. Effectively, each bucket is assigned a block of memory, and the points we want to add into the bucket are copied into this memory block. This is essentially a radix sort, with the following procedure:
- Iterate over every scalar, computing the 'windowed non-adjacent form' bit slices required for each round
- For each round, iterate over the wnaf slices, counting the number of entries assigned to each bucket
- Use the bucket counts to allocate memory for each bucket (let's call these bucket blocks)
- For each round, iterate over the wnaf slices, using the wnaf slice value to copy the associated point into the relevant bucket block
Once this has been achieved, we can then, for each bucket, iterate over the bucket's associated points, and add the point into the bucket accumulator.
The benefits of this approach are:
- Easily parallelizable, threads / gpu cores can be assigned a range of buckets to iterate over
- Reduced control flow in main loop - we currently have to check whether a bucket is empty for iteration of our main loop - with this version, we can skip this step and initialize each bucket to contain the first bucket point
- Concretely fewer field multiplications: when adding the second bucket point into a bucket accumulator, both points will have a Z-coordinate of 1. This allows us to use a more efficient point addition algorithm for this special case
Drawbacks of this approach:
- Memory latency will be a problem for the radix sort - each bucket will have a size that is greater than the L1 cache for all but the smallest of PLONK circuits. Until we have a working implementation further optimization is premature, but if this becomes a problem we can use a cache-optimized radix sort (more sorting rounds, but each round works on data that's in the L1 cache)
This solution is unnecessary complex, uses a lot of memory, has a significant serial preprocessing step that limits parallelism (see Amdahl’s Law) and will worsen all memory bandwidth issues.
Instead we can combine the following 2 papers to create a simple per-thread scheduler with bounded memory usage:
- FPGA Acceleration of Multi-Scalar Multiplication: CycloneMSM
Kaveh Aasaraai, Don Beaver, Emanuele Cesena, Rahul Maganti, Nicolas Stalder and Javier Varela, 2022
https://eprint.iacr.org/2022/1396.pdf
Takeaways: Scheduler idea + collision probability analysis - cuZK: Accelerating Zero-Knowledge Proof with A Faster Parallel Multi-Scalar Multiplication Algorithm on GPUs
Tao Lu, Chengkun Wei, Ruijing Yu, Chaochao Chen, Wenjing Fang, Lei Wang, Zeke Wang and Wenzhi Chen, 2022
https://eprint.iacr.org/2022/1321.pdf
Takeaway: Parallelism over buckets by considering MSM as a sparse Matrix-Vector operation.
With these, you can process a MSM with no mandatory preprocessing (no wNAF → Booth encoding, optional endomorphism, no radix sort) and limited allocation.
The first important piece is an efficient encoding of:
- which point to accumulate
- in which bucket
- what sign is the point
This can be done in a 64-bit bitfield (4 bytes) that can support all relevant sizes for the years to come.
type ScheduledPoint* = object
bucket {.bitsize:26.}: int64 # Supports up to 2²⁵ = 33 554 432 buckets and -1 for the skipped bucket 0
sign {.bitsize: 1.}: int64
pointID {.bitsize:37.}: int64 # Supports up to 2³⁷ = 137 438 953 472 pointsThen each thread will allocate a scheduler that will be responsible of a bucket range (and not point range). This avoids data races as this way 2 different threads will never try to add points in the same bucket at the same time.
Each scheduler will contain 2 queues, a queue A of independent points and a queue B of points already in A. When A reaches a certain threshold, to amortize batch inversion, queue A is processed. Note that those queue stores only the ScheduledPoint descriptor, 8 bytes) instead of a full (potentially negated) affine point (64 bytes) and the target bucket (4 bytes), dividing memory usage by at least 9 compared to Barretenberg, and reducing memory bottlenecks.