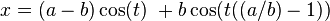Using:
Where t increases monotonically, and k can be varied with the slider below, the (x,y) co-ordinates sweep out the curve of a distressed Cardioid. When k = 0.5 the curve sweeps out a perfect Cardioid.
The state and rendering are maintained as separate concerns using the Big-bang library. Furthermore, the sliders at the bottom of the canvas area are implemented as self-contained composite big-bang components in their own right: as soon as a change event occurs on one, the slider re-renders the display value and emits the new value on the supplied channel.