https://mjambon.com/2016-07-23-moving-percentile/ の和訳です。
これは exponential moving average (指数平滑移動平均)と同じ制約によって駆動する手法ですが 中央値やパーセンタイル値のための手法です。 時間によって分布の変化するような観察結果の無限ストリームにおける中央値などのパーセンタイルのトラッキングのためにアルゴリズムを示します。 自ら課した制約はメモリに直近のNの観察結果を明示的に持つことを与えません。 私達のアルゴリズムでは、予測されたパーセンタイルのアップデートのコストはO(1)でそのメモリ使用量もまたO(1)です。 r で示される単一のパラメータはユーザによって定義され、(信号の分布の変化に対する)accuracyとreactivityの間のトレードオフを表現しています。
注釈: このドキュメントでは全ての数列と配列は0から始まります。
固定のウィンドウの長さ N であるとすると、0 〜 (N - 1)のインデックスが付けられた最新のNの観測結果のソートされた配列 W を維持することは比較的簡単です。
p パーセンタイルは floor((N-1)p) と ceil((N-1)p) のインデックスで見つけられる値のペアを見つけて、
その平均を取ることによって、そのウィンドウを通して正確に計算されます。
例えば、ウィンドウの長さは100を使った時の中央値 m (0.5 percentile)は 100かより多くの観測結果読んだら次のように計算されます。
このようなアルゴリズムは、一般的に100より多くの、直近Nの値を保存する必要があり、これは受け入れられるものではありません。
指数平滑移動平均は過去の観測結果に基づく加重平均で、直近の観測結果の重みはパラメータ r (0 < r <= 1) に固定され、他の値への重みは (1 - r) 倍の重みになります。
floor(1/r) + 1 個かより多くの観測結果を読んだ後、その観測結果 i の移動平均は次のように計算されます。
i < floor(1/r) の初期段階では、 m_iはこれまでの全ての観測結果の平均によって計算されます。 その根拠は、その直近の重みは、過去の観測結果のいずれの重みよりも小さくなることなく、rに限りなく近い可能性があるということです。(※) これは、m_-1に永続的な影響を持つ任意の推測を持つことを避けるためです。 この初期フェーズが終わったmの更新は次のように行われます。
この指数平滑移動平均アルゴリズムは 下で記されるmoving percentile アルゴリズムにおいて信号の標準偏差を推測するために使われます。
※訳者注 文意が取れなかった
変数 m によって p パーセンタイルは表されます。 それは、観測値x_0の値によって初期化されます。
個族の繰り返しによって、後に記される値 δ によって次のように更新されます。
else if x_i > m_i-1 then
もし、δが大きすぎず小さすぎないなら、mはパーセンタイルの良い推測になっています。 δの良い値を選ぶことは、pパーセンタイルの周りの値の分布に依存しています。 δの過剰な値はmにおける大きなジャンプを結果し、正確さを制限します。 一方でδが小さすぎる場合は、妥当な長さのウィンドウを用いて正確に計算されたpパーセンタイルに収束するのに時間が掛かりすぎるかもしれません。
正確さと収束スピードのトレードオフを表現するために、ユーザが選んだ定数 r と入力信号の推測された標準偏差の積でδを表現します。
ここで、σ_i は μはxの移動平均によって推測され、数列の移動平均 (μ_i - x_i)^2 によって推測される分散の平方根です。
多くのアプリケーションにおける r の妥当な値の範囲は 0.001 〜 0.01であることを見つけました。
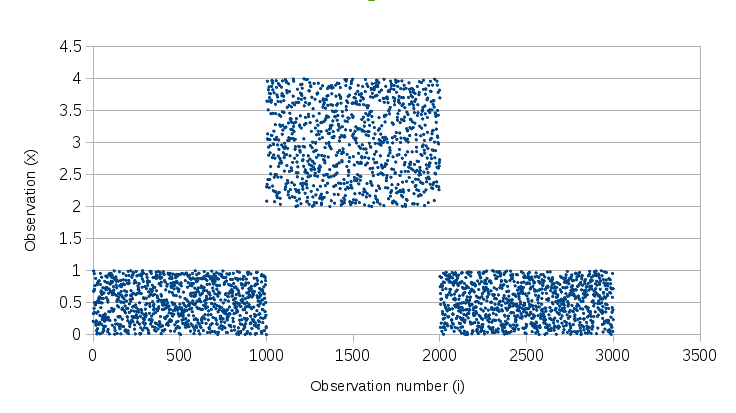
次のチャートは 3フェーズにランダムで生成されたサンプリング信号を示しています。
- phase 1 (0 - 999): Uniform(0, 1); expected 0.9 percentile = 0.9
- phase 2 (1000-1999): Uniform(2,4); expected 0.9-percentile = 3.8
- phase 3 (2000-2999): Uniform(0,1); expected 0.9 percentile = 0.9
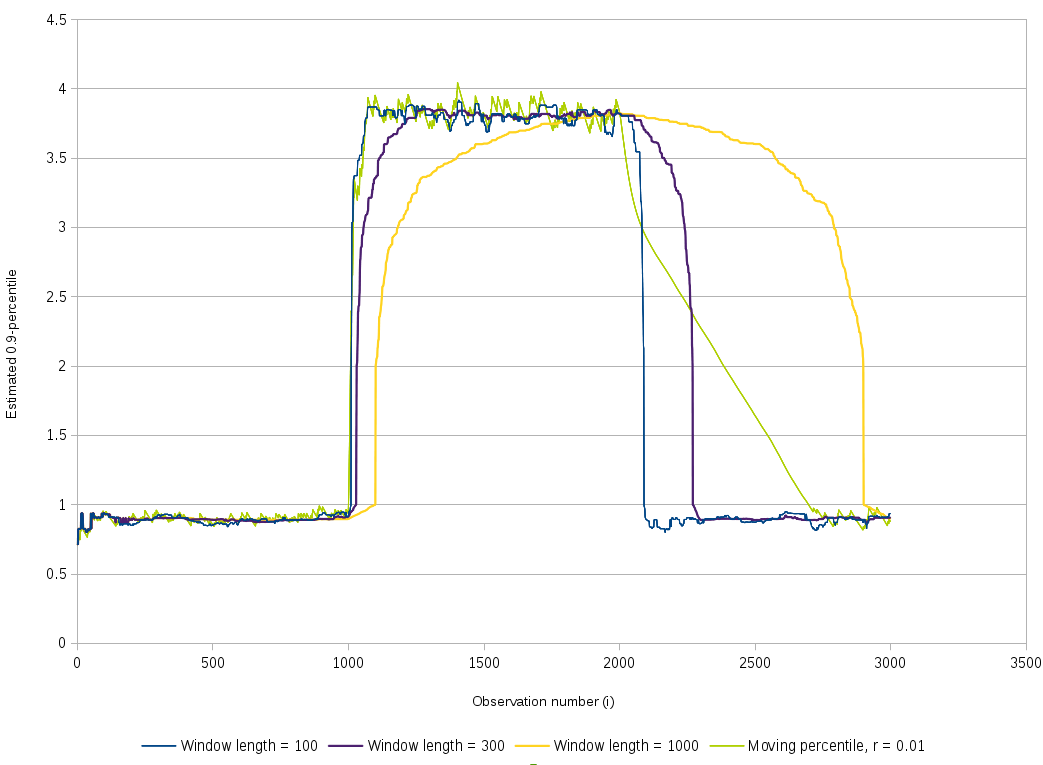
ウィンドウベースのパーセンタイル推測器と私達の移動パーセンタイルによる出力は次のように示されます。
我々の移動0.9パーセンタイルは, 緑のチャートで示されており、信号が上向きにシフトした時俊敏に反応しています。 なぜならそれぞれの更新は δ/0.1によって上向きに移動平均をシフトするからです。しかしながら、信号が下向きにシフトした時、反応するのにより多くの時間が掛かっています。。 なぜならそれぞれの更新で δ/0.9によって下向きにシフトするからで、上向きと比べて9倍小さいです。 加えて、下向きのシフトは最初はとても急でその後よりゆるやかになります。 これは標準偏差の遅延された更新によるもので、推定されたσが追いついて2で割られた時に、δは2によって割られて、phase 3の新しい分布を反映しています。
サンプル実装はGitHubにあります。