You should use this version instead; it's better.
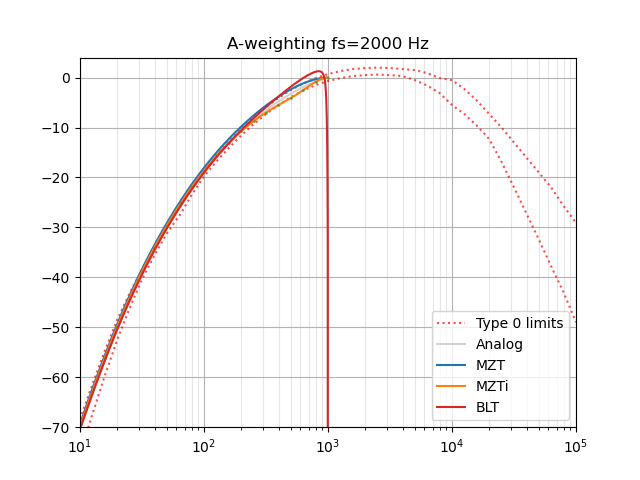
Note that this uses a bilinear transform and so is not accurate at high frequencies.
Apply an A-weighting filter to a sound stored as a NumPy array.
Use Audiolab or other module to import .wav or .flac files, for example. http://www.ar.media.kyoto-u.ac.jp/members/david/softwares/audiolab/
Translated from MATLAB script (BSD license) at: http://www.mathworks.com/matlabcentral/fileexchange/69






@endolith
Personnaly, I am trying to build-up a library that wraps up a few key functions for quick audio files analyses. I've picked stuff from librosa, scipy, etc and got your code from some colleague's scripts. That's the reason why I went for that first version.
Thks for the info about the MZTi method, I'll look for a little help around to check what I can do with it.
Regards