|
""" |
|
Python translation of http://sethares.engr.wisc.edu/comprog.html |
|
""" |
|
import numpy as np |
|
|
|
|
|
def dissmeasure(fvec, amp, model='min'): |
|
""" |
|
Given a list of partials in fvec, with amplitudes in amp, this routine |
|
calculates the dissonance by summing the roughness of every sine pair |
|
based on a model of Plomp-Levelt's roughness curve. |
|
|
|
The older model (model='product') was based on the product of the two |
|
amplitudes, but the newer model (model='min') is based on the minimum |
|
of the two amplitudes, since this matches the beat frequency amplitude. |
|
""" |
|
# Sort by frequency |
|
sort_idx = np.argsort(fvec) |
|
am_sorted = np.asarray(amp)[sort_idx] |
|
fr_sorted = np.asarray(fvec)[sort_idx] |
|
|
|
# Used to stretch dissonance curve for different freqs: |
|
Dstar = 0.24 # Point of maximum dissonance |
|
S1 = 0.0207 |
|
S2 = 18.96 |
|
|
|
C1 = 5 |
|
C2 = -5 |
|
|
|
# Plomp-Levelt roughness curve: |
|
A1 = -3.51 |
|
A2 = -5.75 |
|
|
|
# Generate all combinations of frequency components |
|
idx = np.transpose(np.triu_indices(len(fr_sorted), 1)) |
|
fr_pairs = fr_sorted[idx] |
|
am_pairs = am_sorted[idx] |
|
|
|
Fmin = fr_pairs[:, 0] |
|
S = Dstar / (S1 * Fmin + S2) |
|
Fdif = fr_pairs[:, 1] - fr_pairs[:, 0] |
|
|
|
if model == 'min': |
|
a = np.amin(am_pairs, axis=1) |
|
elif model == 'product': |
|
a = np.prod(am_pairs, axis=1) # Older model |
|
else: |
|
raise ValueError('model should be "min" or "product"') |
|
SFdif = S * Fdif |
|
D = np.sum(a * (C1 * np.exp(A1 * SFdif) + C2 * np.exp(A2 * SFdif))) |
|
|
|
return D |
|
|
|
|
|
if __name__ == '__main__': |
|
from numpy import array, linspace, empty, concatenate |
|
import matplotlib.pyplot as plt |
|
|
|
""" |
|
Reproduce Sethares Figure 3 |
|
http://sethares.engr.wisc.edu/consemi.html#anchor15619672 |
|
""" |
|
freq = 500 * array([1, 2, 3, 4, 5, 6]) |
|
amp = 0.88**array([0, 1, 2, 3, 4, 5]) |
|
r_low = 1 |
|
alpharange = 2.3 |
|
method = 'product' |
|
|
|
# # Davide Verotta Figure 4 example |
|
# freq = 261.63 * array([1, 2, 3, 4, 5, 6]) |
|
# amp = 1 / array([1, 2, 3, 4, 5, 6]) |
|
# r_low = 1 |
|
# alpharange = 2.0 |
|
# method = 'product' |
|
|
|
n = 3000 |
|
diss = empty(n) |
|
a = concatenate((amp, amp)) |
|
for i, alpha in enumerate(linspace(r_low, alpharange, n)): |
|
f = concatenate((freq, alpha*freq)) |
|
d = dissmeasure(f, a, method) |
|
diss[i] = d |
|
|
|
plt.figure(figsize=(7, 3)) |
|
plt.plot(linspace(r_low, alpharange, len(diss)), diss) |
|
plt.xscale('log') |
|
plt.xlim(r_low, alpharange) |
|
|
|
plt.xlabel('frequency ratio') |
|
plt.ylabel('sensory dissonance') |
|
|
|
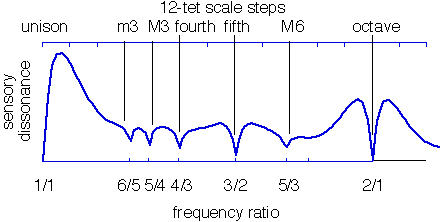
intervals = [(1, 1), (6, 5), (5, 4), (4, 3), (3, 2), (5, 3), (2, 1)] |
|
|
|
for n, d in intervals: |
|
plt.axvline(n/d, color='silver') |
|
|
|
plt.yticks([]) |
|
plt.minorticks_off() |
|
plt.xticks([n/d for n, d in intervals], |
|
['{}/{}'.format(n, d) for n, d in intervals]) |
|
plt.tight_layout() |
|
plt.show() |



@endolith I didn't know that
scipy.io.wavfile.writewouldn't automatically scale it so that it doesn't clip. I re-synthesized the scales, replacing the links in my comments above. They sound more likeIPython.display.Audio, which presumably does scale to avoid clipping. Thanks!I haven't heard of tritave (until now). Whereas that only admits odd-numbered small integer ratios of frequencies, this "onium scale" only admits perfect-square small integer ratios of frequencies. Whereas the tritone is consonant with overtones of equally spaced, odd-numbered frequency ratios, the onium scale is consonant with overtones of$1/n$ -spaced frequencies. Equally spaced frequencies/energies of waves are common in physics, from plucked strings and air vibrating in clarinets to excitations of the fields that make particles themselves—we call particles "things" because fundamental fields have an energy spectrum of equally spaced levels: "one particle," "two particles," and "three particles" are excitations of a field into the 1×mass, 2×mass, and 3×mass energy levels. Equal spacing is so ubiquitous because it's the wave solution to a parabolic potential energy curve, and any smooth minimum can be approximated by a parabola if you zoom in enough. (For example, the Higgs field is not purely parabolic, but it's approximately parabolic around its minimum energy, so Higgses can be created as particles.)
The$1/n$ -spaced frequency/energy spectrum is a solution of $-1/r$ potentials, which are also pretty common, but not common macroscopically. An orbiting planet has the same $-1/r$ potential as a Hydrogen atom, but a planet is in too high of an energy state to be wave-like, the way that vibrations on a string are, pressure waves in air are, and the probability distribution of an electron's position is. Other particles have been electomagnetically bound to protons, such as muons in muonium, and other particles have been bound to each other, such as electrons and positrons in positronium. Quarkonia almost count as another example, except that the potential between quarks is only $-1/r$ in the small-$r$ limit.
But generalizing from the tritave's picking out small odd-integer ratios and the onium scale's picking out small squared-integer ratios, why not some other restriction on the integers, such as cubes or only admitting prime numbers? One could work backward to find the timbre that makes prime-numbered ratios consonant. A quantum particle in a box (physically realized in a quantum well laser, for instance) has an$n^2$ energy spectrum, which would pick out a different set of consonant intervals.
I found my way here from listening to Gamelan music while washing the dishes, to looking up some of the theory behind it, to this video:
https://youtu.be/ksX-saQVL40
which applied Plomp and Levelt's dissonance curve to the instruments' timbre and derived something close to the Slendro and Pelog scales. I was dumbfounded: this was the answer to a long-standing question of mine—why do we pick the musical scales that we do? Apart from Gamelan, most cultures pick subsets of the same set of small-integer ratios, which seemed like more agreement than I would expect. The words and even phonemes of languages around the world are a lot more diverse than the choice of pitches in music. This explanation—that it's a relatively simple, universal dissonance curve (perhaps hard-wired in our biology), integrated over the overtones of the instruments that we use—not only explains the common scales, but outliers like Gamelan. It boils down to biology (maybe the frisson of dissonance is the "uncanny valley" between putting two pitches in the same category and putting them in different ones? brains like categorizing continuous quantities...) and what the common instruments are, and the choice of instruments accounts for cultural variance. Most instruments have equally spaced harmonics, because of common physics, so their scales are similar, but the keys in Gamelan instruments are suspended, so they have a different timbre and therefore a different consonant scale.
The video also pointed to Sethares's book, which is how I ended up here. I'm still reading the book, but I had to try the dissonance summation procedure on different timbres. (Thanks for porting it to Python! That made it easier to just pick it up and try things out!) I also read Plomp and Levelt's paper. They didn't explain the procedure in much detail (and how you weight the sum by loudness has been debated since), and they didn't mention Gamelan. It's a much stronger theory when it's shown to work for an outlier as well as the common scales. Sethares's book includes Gamelan instruments and scales in many sections—is he the one who first applied Plomp-Levelt dissonance to Gamelan? Because that's an important step that clinches this very powerful explanation of where scales come from.
@BrandonKMLee, chapter 5 of Sethares's book (Tuning, Timbre, Spectrum, Scale by W. Sethares) has a survey of different dissonance measures, some very different from the Plomp-Levelt measure (Tonal Consonance and Critical Bandwidth R.Plomp & W.J.M.Levelt), including one that uses entropy. (I haven't read that one yet, but I'm getting there.) All of them are about the harmony of notes and intervals when choosing frequencies to include in a scale, not the notes in a piece of music, drawn from a common scale. That is, if you're trying to make an index over musical pieces that are all in the same 12-tone equal-tempered scale (i.e. nearly all Western music), I don't think that index could distinguish them. I guess some intervals in the 12-tone scale are more consonant than others, particularly where the equal-temperament makes them miss the minima of the curves above, and an index could rate songs differently if they use more of these "bad notes." Or even if the scale is just-tempered, usage of smaller integer ratios (fourth and fifth) could be scored differently from usage of the others.