My third neural network experiment (second was FIR filter). DFT output is just a linear combination of inputs, so it should be implementable by a single layer with no activation function.
Animation of weights being trained:
Red are positive, blue are negative. The black squares (2336 out of 4096) are unused, and could be pruned out to save computation time (if I knew how to do that).
Even with pruning, it would be less efficient than an FFT, so if the FFT output is useful, probably best to do it externally and provide it as separate inputs?
This at least demonstrates that neural networks can figure out frequency content on their own, though, if it's useful to the problem.
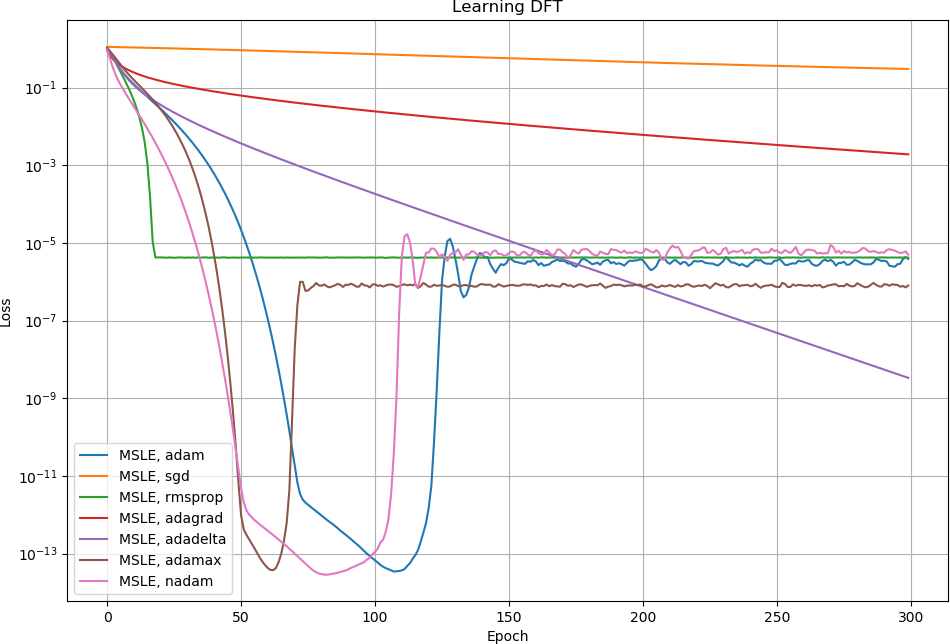
The loss goes down for a while but then goes up. I don't know why:






Have you considered the 2D DFT? I'm wondering if the same network (with higher capacity) would still work.