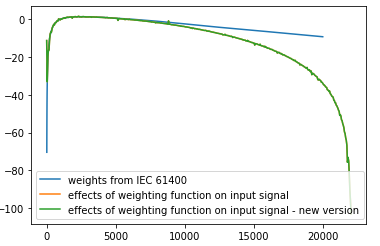
You should use this version instead; it's better.
Note that this uses a bilinear transform and so is not accurate at high frequencies.
Apply an A-weighting filter to a sound stored as a NumPy array.
Use Audiolab or other module to import .wav or .flac files, for example. http://www.ar.media.kyoto-u.ac.jp/members/david/softwares/audiolab/
Translated from MATLAB script (BSD license) at: http://www.mathworks.com/matlabcentral/fileexchange/69
| #!/usr/bin/env python | |
| # -*- coding: utf-8 -*- | |
| """ | |
| Translated from a MATLAB script (which also includes C-weighting, octave | |
| and one-third-octave digital filters). | |
| Author: Christophe Couvreur, Faculte Polytechnique de Mons (Belgium) | |
| couvreur@thor.fpms.ac.be | |
| Last modification: Aug. 20, 1997, 10:00am. | |
| BSD license | |
| http://www.mathworks.com/matlabcentral/fileexchange/69 | |
| Translated from adsgn.m to Python 2009-07-14 endolith@gmail.com | |
| """ | |
| from numpy import pi, polymul | |
| from scipy.signal import bilinear | |
| def A_weighting(fs): | |
| """Design of an A-weighting filter. | |
| b, a = A_weighting(fs) designs a digital A-weighting filter for | |
| sampling frequency `fs`. Usage: y = scipy.signal.lfilter(b, a, x). | |
| Warning: `fs` should normally be higher than 20 kHz. For example, | |
| fs = 48000 yields a class 1-compliant filter. | |
| References: | |
| [1] IEC/CD 1672: Electroacoustics-Sound Level Meters, Nov. 1996. | |
| """ | |
| # Definition of analog A-weighting filter according to IEC/CD 1672. | |
| f1 = 20.598997 | |
| f2 = 107.65265 | |
| f3 = 737.86223 | |
| f4 = 12194.217 | |
| A1000 = 1.9997 | |
| NUMs = [(2*pi * f4)**2 * (10**(A1000/20)), 0, 0, 0, 0] | |
| DENs = polymul([1, 4*pi * f4, (2*pi * f4)**2], | |
| [1, 4*pi * f1, (2*pi * f1)**2]) | |
| DENs = polymul(polymul(DENs, [1, 2*pi * f3]), | |
| [1, 2*pi * f2]) | |
| # Use the bilinear transformation to get the digital filter. | |
| # (Octave, MATLAB, and PyLab disagree about Fs vs 1/Fs) | |
| return bilinear(NUMs, DENs, fs) |
| import sys | |
| from scipy.signal import lfilter | |
| import numpy as np | |
| from A_weighting import A_weighting | |
| try: | |
| import soundfile as sf | |
| except ImportError: | |
| from scikits.audiolab import wavread | |
| # (scipy.io.wavfile can't read 24-bit WAV) | |
| def rms_flat(a): # from matplotlib.mlab | |
| """ | |
| Return the root mean square of all the elements of *a*, flattened out. | |
| """ | |
| return np.sqrt(np.mean(np.absolute(a)**2)) | |
| if len(sys.argv) == 2: | |
| filename = sys.argv[1] | |
| else: | |
| filename = 'noise.wav' | |
| try: | |
| x, fs = sf.read(filename) | |
| except NameError: | |
| x, fs, bits = wavread(filename) | |
| print(filename) | |
| print('Original: {:+.2f} dB'.format(20*np.log10(rms_flat(x)))) | |
| b, a = A_weighting(fs) | |
| y = lfilter(b, a, x) | |
| print('A-weighted: {:+.2f} dB'.format(20*np.log10(rms_flat(y)))) |
So I'm looking at my "improved" version from 2018, which is based on the MZTi method and it does indeed have better frequency response at high frequencies:
But I think the reason I didn't push it was because I wasn't sure I was doing it right. "Since the mapping wraps the s-plane's jω axis around the z-plane's unit circle repeatedly, any zeros (or poles) greater than the Nyquist frequency will be mapped to an aliased location." And I'm not sure if those need to be removed first, depending on the sampling rate, etc. At lower sample rates it gets worse, so it still needs some work. (Also the aliased Nyquist tail could be pushed down a bit to improve the overall average accuracy.)
This paper just describes the same BLT solution as this gist, and has a table of the minimum required sample rate to meet the tolerances:
| A-weighting | C-weighting | |
|---|---|---|
| IEC 61672-1 Class 1 | 35 kHz | 35 kHz |
| IEC 61672-1 Class 2 | 20 kHz | 20 kHz |
| ANSI S.1-43 Type 0 | 71 kHz | 72 kHz |
| ANSI S.1-43 Type 1 | 35 kHz | 35 kHz |
| ANSI S.1-43 Type 2 | 20 kHz | 20 kHz |
There are probably other papers that describe better methods, I should look for them.
@ThomQu @annezhangxue @shangyan0517 @frgos2 @masahf @mankind-nil @Zeokat
Can you all tell me how you use this code so I can improve it? I tried to fold it into a library with other related functions like THD+N calculators, etc. But people still comment on this gist, so maybe it's better for it to be self-contained? I assume you are all using the digital filter version and not the analog filter coefficients?
Personnaly, I am trying to build-up a library that wraps up a few key functions for quick audio files analyses. I've picked stuff from librosa, scipy, etc and got your code from some colleague's scripts. That's the reason why I went for that first version.
Thks for the info about the MZTi method, I'll look for a little help around to check what I can do with it.
Regards
Ok, so maybe I should just make an installable weighting filter library that does nothing else, and then you could use it in yours, etc? I tried combining it with other things like frequency estimation and THD calculation, but maybe those are too unrelated to combine.
I was asked on Stack Exchange for my MZTi code, even if crude, so here it is.
I don't think it's correct at very low sample rates, because of aliasing, but should be better at the typical 44.1 or 48 kHz. It's definitely wrong below fs = 2.5 kHz. In between, I think the MZTi zeroes are forcing it into compliance despite being poorly-transformed.
I don't think it makes much practical difference in dB levels vs the BLT method, by the way.
# Poles and zeros for analog filter from specification
z, p, k = ABC_weighting('A')
# Matched Z Transform:
T = 1/fs
z_MZT = np.exp(z*T) # 4
p_MZT = np.exp(p*T) # 6
k_MZT = k * ((np.prod(2*pi*1000 - z)/
np.prod(2*pi*1000 - p)) *
(np.prod(1 - exp(p*T - 2*pi*1000*T)))/
np.prod(1 - exp(z*T - 2*pi*1000*T)))
# Tweak gain to actual magnitude response TODO: Why is this necessary?
w_MZT, h_MZT = signal.freqz_zpk(z_MZT, p_MZT, k_MZT, [1000/(fs/2)*pi])
k_MZT /= abs(h_MZT)
w = np.array([pi/3, 2*pi/3])
H = abs(signal.freqs_zpk(z, p, k, w*fs)[1] /
signal.freqz_zpk(z_MZT, p_MZT, k_MZT, w)[1]) # relative magnitude error
# MZTi method of 0, 1/3, 2/3 Nyquist will not work, since response at 0 is 0.
H = np.concatenate(([1], H))
b1 = 0.5 * (H[0] - sqrt(H[0]**2 - 2*H[1]**2 + 2*H[2]**2))
b2 = (3 * (H[0] - b1) -
sqrt(-3*H[0]**2 + 12*H[1]**2 - 6*H[0]*b1 - 3*b1**2 + 0j)
) / 6
b0 = H[0] - b1 - b2
b = np.array([b0, b1, b2])
z_correct = np.roots(b)
# TODO: Is this right?
z_MZTi = np.concatenate((z_MZT, z_correct))
p_MZTi = p_MZT
k_MZTi = k_MZT
# Tweak gain to actual magnitude response again TODO: Why?
w_MZTi, h_MZTi = signal.freqz_zpk(z_MZTi, p_MZTi, k_MZTi, [1000/(fs/2)*pi])
k_MZTi /= abs(h_MZTi)
And the reference is https://www.khabdha.org/wp-content/uploads/2008/03/optimizing-the-magnitude-response-of-mzt-filters-mzti-2007.pdf
so maybe I should just make an installable weighting filter library that does nothing else
and maybe include bilinear as an option so people can compare with the results of other software?
FYI, the MZTi version is accurate down to about 2.5 kHz:
@endolith your graph are very interresting !
how do you graph the type 0 limits ?
Thank you endolith !
i just found the table from standard, and i'm little bit surprised because the values are not exactly the same.
do you still have the original table ? (i do not have the standard at my side, so i use google to find parts of it 🙃)
thank a lot !
@endolith one more question about MZTi, have you push this improvement somewhere ? (i haven't found it ...)
My goal is to use the resulting coefficient in a microcontroller based hardware with IIR/FIR filtering functions, do you know if MZTi coefficient usable in those cases ? (i'm beginner in signal processing)
thank you !
@rickou The values I used are from https://law.resource.org/pub/us/cfr/ibr/002/ansi.s1.4.1983.pdf
I think I only posted the MZTi code above https://gist.github.com/endolith/148112?permalink_comment_id=3928477#gistcomment-3928477
and again I have qualms about it, I'm not sure if it's handling the high-frequency poles/zeros correctly.
Thank you ! now i understand the differences..
About the MZTi, i already read your post, do you have any clues that could explain why the high frequency poles/zeros could not be good ?
What can be wrong on signal or on response ?
Have you made some test with real waveforms ?
do you have any clues that could explain why the high frequency poles/zeros could not be good ?
MZT appeals to me for high sample rates because the A-weighting filter is defined by precise pole locations, so it feels right to transform them this way and get a similar response. The problem is that when the sampling rate is too low, they are outside the Nyquist range and it introduces error. The i stage will then correct for this as much as possible, so it's still accurate down to 2.5 kHz, but it just feels kind of wrong to me to produce the wrong response and then patch over it with this bandaid.
hum.. i think i understand.. to be honest i'm not so comfortable with digital filtering.
i have implemented this filter in embedded software and i will made some tests in next weeks in real situation comparing my implementation and sonometer.
but my preliminary tests on bench shows nothing bad. (i'm using 20k sample rate)
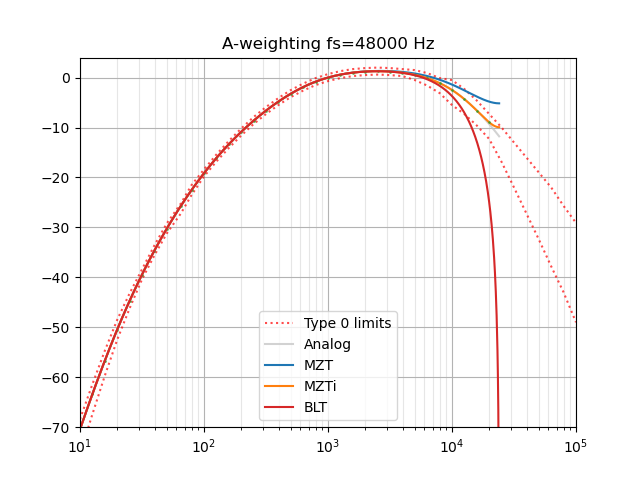
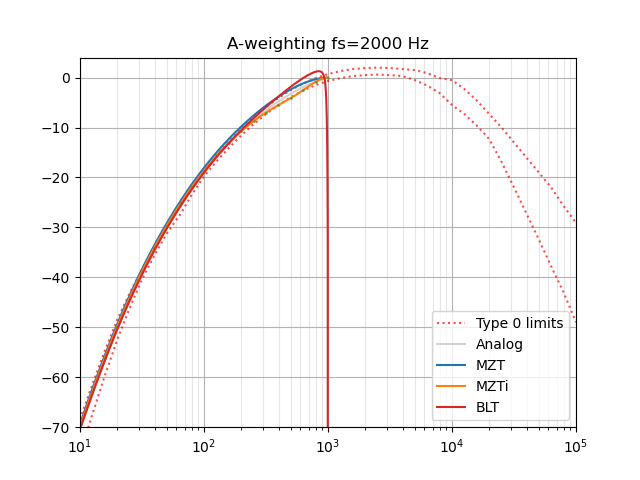
OK I should have mentioned first that my input signal is sampled at 44 kHz,
The "weights from IEC 61400" curve is just the plotting of the norm's formula:
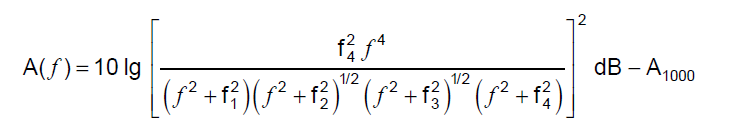
i.e. the difference in dB between between an A_weighted spectrum and the same spectrum without weighting
So when I apply the A_weighting function over my white-noise signal, I get a filtered signal in return. I would expect that when I plot its spectrum minus the original spectrum ("effects of weighting function" plot), I would get the same response as the "weights from IEC 61400", at least until 20 kHz (fs/2).
The "polynom" curve was the plotting of NUMs/DENs from this first code's version, applied to the frequencies array and 10-logged:
poly = 10*np.log10(np.polyval(NUMs,f_norm)/np.polyval(DENs,f_norm))
but forget it, I have to dig on filtering's theory (I'm not a spectialist), plotting that and expecting it to be similar to "weights from IEC 61400" might not be relevant...
I've just tested your newer version, the results are indeed equal to this one's.
