You should use this version instead; it's better.
Note that this uses a bilinear transform and so is not accurate at high frequencies.
Apply an A-weighting filter to a sound stored as a NumPy array.
Use Audiolab or other module to import .wav or .flac files, for example. http://www.ar.media.kyoto-u.ac.jp/members/david/softwares/audiolab/
Translated from MATLAB script (BSD license) at: http://www.mathworks.com/matlabcentral/fileexchange/69


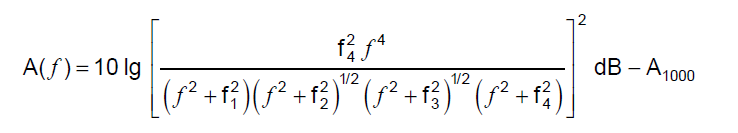
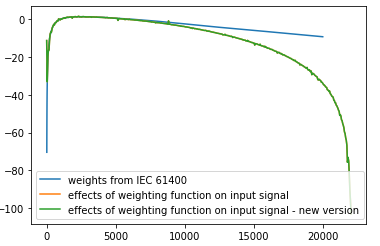
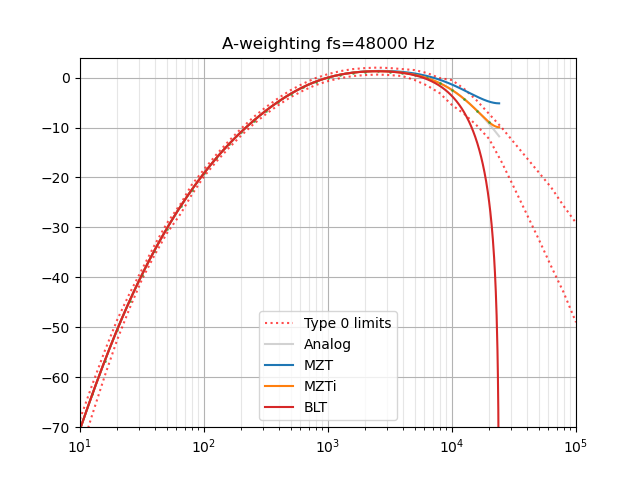




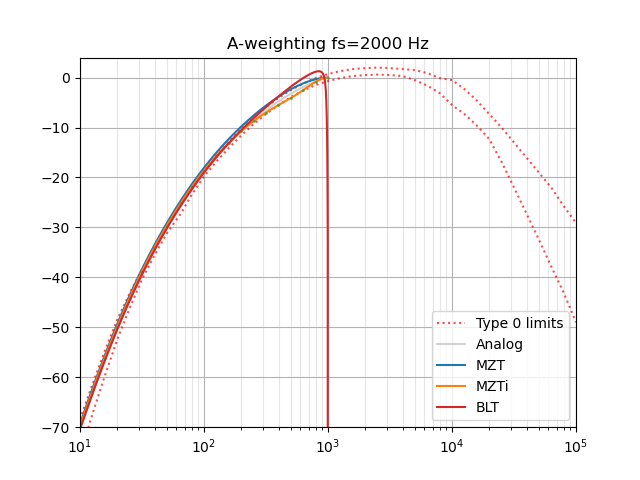


Many thanks endolith! I am using your A_weighting.py script in some code I have started drafting, and I have included it in my repository: https://github.com/acuti/acuSLM. I hope you are ok with it. If not, please let me know.